GM（1，1）模型和Verhulst模型的改进及其应用＊

肖岚菁，刘红良

（1.长沙市南雅中学，湖南长沙 410129；2.湘潭大学数学与计算科学学院，湖南湘潭 411105）

GM（1，1）模型和Verhulst模型的改进及其应用＊

肖岚菁1，刘红良2

（1.长沙市南雅中学，湖南长沙 410129；2.湘潭大学数学与计算科学学院，湖南湘潭 411105）

基于残差修正对GM（1，1）模型和Verhulst模型进行改进，利用所改进的模型分别对湖南省固定资产投资和水稻产量进行预测.预测结果表明，改进后的模型模拟精度明显优于原来模型模拟精度，改进的方法分别更适合于固定资产投资和水稻产量的预测.

回归分析；灰色预测；GM（1，1）模型；Verhulst模型

随着社会经济的发展，现代科技的不断进步，人们越来越重视预测在生活中的应用.目前，常用的预测模型包括回归模型、指数平滑法、灰色GM（1，1）模型及Verhulst模型等［1－6］，这些模型各有优势，被广泛应用于国民经济、风电功率、用电负荷及投资等许多科学经济领域的预测中.但这些模型若单独使用，则存在预测精度不高等缺点.为此，笔者首先综合使用这些模型，基于残差修正来改进GM（1，1）模型及Verhulst模型.

固定资产投资是建造和购置固定资产的经济活动，是社会固定资产再生产的主要手段，在整个社会投资中占据主导地位.因此，预测固定资产投资总额成为社会经济研究中的重要内容.为了较准确地预测湖南省2013年每个月份固定资产投资所需资金总额，有必要建立湖南省的固定资产投资模型.一个社会的固定资产投资往往受到许多因素的制约，而且这些因素之间又保持着错综复杂的联系，因此，运用结构性的因果模型分析和预测往往比较困难.

粮食产业作为农业的重要组成部分，其意义不言而喻.自古以来，无粮则不稳，粮食产量的高低，对稳定中国安定团结的政治局面、顺利开展中国社会主义现代化各项事业建设、构建社会主义和谐社会等都有重要意义.同时，作为粮食安全保障的一个重要组成部分，粮食的产量安全是中国应对国际粮食危机的重要举措之一.因此，无论是对中国目前经济发展状况的认识，还是对未来经济发展的预测，粮食问题的研究都具有十分重要的意义，而合适的粮食预测方法就显得非常重要.

首先研究湖南省水稻产量未来的走势.考虑到湖南省水稻产量呈“S”型序列，因此将基于残差修正的Verhulst模型应用于湖南省水稻产量的预测，这样不仅保留了Verhulst模型［4］的优势和特点，而且比Verhulst模型具有更高的精度.

然后研究湖南省全社会固定资产投资额未来的走势.利用GM（1，1）模型对其预测，得到残差序列，再对残差序列进行回归分析，之后利用残差预测结果修正GM（1，1）模型的预测结果.残差修正后的预测结果误差显著减少，更符合实际情况.

1 GM（1，1）模型的改进

其中a，b为灰参数.进一步可得GM（1，1）模型（1）的参数序列a－＝a，

（b）T的最小二乘估计

对（4）式作一次累减还原计算，得到原始序列X0的GM（1，1）预测模型

这里：β0，β1，...，βp是p＋1个未知参数，称为回归系数；x为解释变量；x（t）为被解释变量.

利用GM（1，1）模型预测模型（5）.用序列观察值减去预测值，可得到残差序列

然后以残差序列ε0为观测时间序列建立回归分析模型，得到残差序列的预测值ε－0（k），k＝1，2，...，从而基于回归分析残差修正的GM（1，1）模型模拟的还原值为

2 Verhulst模型的改进

Verhulst模型是1837年德国生物学家Verhulst在研究生物繁殖规律时提出来的.其基本思想是，生物个体数量呈指数增长，受周围环境的限制，增长速度逐渐放慢，最终稳定在一个固定值.Verhulst模型主要用来描述具有饱和状态的过程，即S形过程.GM（1，1）模型适用于具有较强指数规律的序列，只能描述单调的变化过程，对于非单调的摆动发展序列或有饱和的“S”型序列，若采用该灰色模型则预测误差较大，预测精度不满足实际要求.

引入Verhulst模型［8］

通过类似于获得（3）式的过程，可得Verhulst模型（9）的参数序列＝（a，b ）T的最小二乘估计为＝（BTB）－1BTY，其中

进一步，得到Verhulst模型的时间响应式为

利用Verhulst模型预测，用序列观测值减去预测值，可得到残差序列

3 改进的GM（1，1）模型模型在固定资产投资中的应用

下面以湖南省2012年3—12月的固定资产投资额的实际序列与拟合序列的误差精度分析，来比较GM（1，1）模型（1）和改进GM（1，1）模型（8）的优劣.表1示出湖南省2012年3—12月固定投资额实际数据，数据来源于湖南统计信息网.

表1 湖南省2012年3—12月固定投资额实际数据

首先利用GM（1，1）模型对湖南省固定资产投资额进行预测，由（3）式得模型的系数＝利用（7）式得到残差序列.然后对残差序列进行二次拟合，得到残差序列的关系式为x＝72.25t2－556.92t＋520.02.进一步，利用（8）式得到基于回归分析残差修正的GM（1，1）模型的预测结果.GM（1，1）模型和修正的GM（1，1）模型的预测结果及相对残差如表2所示.表2结果表明，基于回归分析残差修正的GM（1，1）模型的预测结果误差更小，可靠性更高，更适合于固定资产投资的预测.

表2 改进模型与原模型计算结果比较

湖南省2013年1—6月的固定资产投资额预测如表3所示.表3结果表明，改进后的模型预测湖南省固定资产投资趋势将变缓，更适合于实际情况.

表3 预测湖南省2013年1—6月的固定资产投资额万元

4 改进的Verhulst模型在水稻产量中的应用

以湖南省水稻产量为例，该省2002—2009年水稻产量如表4所示，数据来源于湖南统计信息网.由表4可知，其产量数据是呈“S”型增长的［9］，故在不考虑外界环境因素对湖南省今后几年经济作物发展影响的前提下，分别利用Verhulst模型和基于GM（1，1）模型残差修正的Verhulst模型对其进行预测.记（k），（k）和Δ（k）分别表示Verhulst模型的预测结果、绝对误差和相对误差，（k），ε＊（k）和Δ＊（k）分别表示改进Verhulst模型的预测结果、绝对误差和相对误差，所得结果如表5所示.2个模型对湖南省水稻产量的预测趋势如图1所示.

表4 湖南省2002—2009年水稻产量值

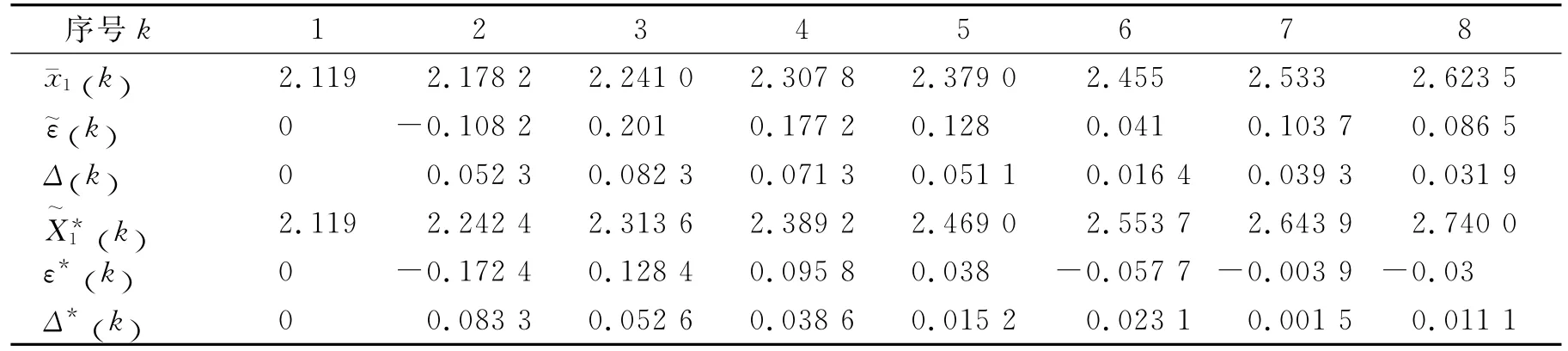
表5 预测结果及误差

由表5及图1结果可知，基于GM（1，1）改进的Verhulst模型模拟结果比Verhulst模型模拟结果更为精确，相对误差更小，且平均相对误差小于0.04，改进的模型更适合对湖南省水稻产量进行预测.

图1 水稻产量预测趋势

5 结语

固定资产和水稻产量由于受自然灾害、经济规律及政策等因素的影响而产生随机波动，波动的周期、幅度和持续时间不是一致的，因此利用残差修正能克服随机因素带来的不确定性.修正后的模型更适合于预测固定资产和水稻产量.

［1］ 郭广猛.用GM（1，1）模型和Verhulst模型进行建筑物沉降预测［J］.岩土工程界，2000，3（10）：33－37.

［2］ 王正宇，王红玲.基于ARIMA模型的我国GDP分析预测［J］.对外经贸，2011，210（12）：107－108.

［3］ 胡丽敏，周新地，黄长军.灰色模型GM（1，1）在益阳市耕地预测中的应用［J］.湖南城市学院学报：自然科学版，2008，17（3）：75－78.

［4］ 周 文.Verhulst模型在城市生活垃圾产量预测中的应用［J］.山西建筑，2012，38（19）：218－220.

［5］ 刘 芳.上海生活垃圾产生量、组成特性及处置对策研究［J］.环境卫生工程，2005，13（2）：37－43.

［6］ 舒 莹.基于灰色预测模型的合肥市城市生活垃圾产量预测［J］.环境科学与管理，2007，32（9）：5－8.

［7］ 邓聚龙.灰色控制系统［M］.武汉：华中理工大学出版社，1988.

［8］ 刘思峰，郭天傍，党耀国，等.灰色系统理论及其应用［M］.北京：科学出版社，1999.

［9］ 易丹辉.数据分析与Eviews应用［M］.北京：中国统计出版社，2002.

（责任编辑 向阳洁）

Improved GM（1，1）Model and Verhulst Model with Their Applications

XIAO Lan-jing1，LIU Hong-liang2
（1.Nanya Middle School of Changsha，Changsha 410129，China；2.School of Mathematics and Computational Science，Xiangtan University，Xiangtan 411105，Hunan China）

The GM（1，1）model and Verhulst model are improved based on residual modification.These improved models are used to predict investment of fixed assets and rice production in Hunan province.The predicting results show that the improved models are better than the previous models and more suitable to predict the investment of fixed assets and rice production.

regression analysis；gray forecast；GM（1，1）model；Verhulst model

O212

A

10.3969／j.issn.1007－2985.2013.05.005

1007－2985（2013）05－0016－05

2013－06－20

湖南省教育厅科学研究项目（11C1220）

刘红良（1979－），男，湖南湘乡人，湘潭大学数学与计算科学学院副教授，博士，主要从事微分方程数值方法及数学建模研究.