关于除数函数与Smarandache k次补数的混合均值＊

黄 炜，马 焱

（1.宝鸡职业技术学院基础部，陕西宝鸡 721013；2.宝鸡文理学院经济管理系，陕西宝鸡 721013）

关于除数函数与Smarandache k次补数的混合均值＊

黄 炜1，马 焱2

（1.宝鸡职业技术学院基础部，陕西宝鸡 721013；2.宝鸡文理学院经济管理系，陕西宝鸡 721013）

对任意的正整数n，Smarandache k次幂补数Ak（n）定义为最小的正整数m，使得mn是完全k次幂数.用解析的方法研究了除数函数τ（n）对补数列Ak（n）的复合函数τ（Ak（n））的混合均值并得到了一个渐近公式.

除数函数；k－次幂补数；均值；渐近公式

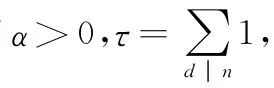
1 引理及证明

文献［5］包含了证明以下引理所需要的基础知识.

引理3 设ε是任意正常数，当σ≥k－1时，有

（1）B（s＋1）在半平面Re s≥k－1＋ε上有界且解析；

证明 对于任意素数p，p的k次补数Ak（pn）为

（2）由定义知Ak（n）是积性函数，又因为τ（Ak（m·n））＝τ（Ak（m））·τ（Ak（n）），τ（Ak（n））也是积性函数，所以由Ak（n）的定义及文献［5］的有关定理有：当σ≥k－1时，τ（Ak（n））的Dirichlet级数为

2 定理及证明

定理1 设x≥1，则有渐近公式

［1］ SMARANDACHE F.Only Problems，Not Solutions［M］.Chicago：Xiquan Publishing House，1993.

［2］ HUANG Wei.An Arithmetical Function and the Power Complements［C］／／Research on Smaramtache Problems in Number Theory.Hexis，2005：123－124.

［3］ 张红莉，王 阳.关于平方补数除数函数的均值［J］.纺织高校基础科学学报，2002（1）：44－46.

［4］ 王 阳.立方幂补数除数函数的均值［J］.数学的实践与认识，2004，34（12）：144－148.

［5］ TOM M APOSTPL.Introduction to Analytic Number Theory［M］.New York：Springer-Verlag，1976.

［6］ PAN C D，PAN C B.Foundation of Analytic Number Theory［M］.Beijing：Science Press，1997.

（责任编辑 向阳洁）

Mean Value of Divisor Function for Smarandache k-Power Complements

HUANG Wei1，MA yan2
（1.Department of Basic Courses，Baoji Vocational and Technical College，Baoji 721013，Shaanxi China；2.Department of Ecomomics and Management，Baoji University of Arts and Sciences，Baoji 721013，Shaanxi China）

Let n be positive integer，the Smarandache k-power complements Ak（n）is defined as the smallest integer m such that mnis perfect k-th power.The mean value ofτ（Ak（n））is studied and an asymptotic formula is given by the analytic integral methods.

divisor function；k-power complement；mean value；asymptotic formula

O156.4

A

10.3969／j.issn.1007－2985.2013.05.002

1007－2985（2013）05－0003－03

2013－01－14

国家自然科学基金资助项目（11071194）；陕西省自然科学基金资助项目（09JK432）

黄 炜（1961－），男，陕西岐山人，宝鸡职业技术学院基础部教授，主要从事解析数论与特殊函数研究；马焱（1963－），女，陕西乾县人，宝鸡文理学院教授，主要从事财务管理研究.