不同地震作用方向下混凝土核心筒基于增量动力分析的抗震性能评估

侯 炜， 史庆轩

(1.华侨大学 土木工程学院，厦门 361021;2.西安建筑科技大学 土木工程学院，西安 710055)

核心筒沿竖向分布刚度变化小，由于电梯间质量相对较小导致水平方向质量分布不均匀。核心筒发生过大变形和严重破坏对整体和局部结构发生失稳乃至倒塌有着重要影响。目前，对单向地震作用下结构的地震反应进行了很多的研究，对高层混合结构也进行了较多分析［1-2］，但对双向或多向地震作用下高层建筑结构的地震反应分析尚较少。文献［3］认为，无论是规则结构还是不规则结构，在多向地震作用下的结构响应要比单向水平地震动作用下的结构响应大。因此，选择合适的输入地震输入，进行高层建筑结构在双向或多向地震作用下的地震反应分析，考察地震入射角和竖向地震分量对结构地震反应的影响，建立双向或多向地震效应的组合方法等有待进行深入的研究。目前，双向或三向地震作用下对结构构件已进行了一定的研究工作，但多集中于L形截面柱、L形截面短肢剪力墙等构件和框架-核心筒结构等［4-6］，而对混凝土核心筒单元在双向地震作用下的损伤演化、性能评估等研究缺乏。考虑地震地面运动方向的未知性和随机性，本文研究不同水平地震不同输入方向作用下核心筒各类构件损伤演化过程，利用时程分析法对核心筒进行各种情况下的地震作用效应计算。并通过输入斜向方向地震记录，基于单条地震记录的IDA方法对核心筒进行抗震性能评估，同时与单向水平地震IDA法抗震性能评估结果作了对比。

1 增量动力分析

增量动力分析方法(IDA方法)由Bertero［7］提出，已被美国FEMA列入设计/评估规程中(FEMA350，FEMA351)，用来评估结构在不同地震作用下的抗震性能。IDA方法最基本的应用形式为将同一条地震波的峰值加速度按一定比例逐级放大，对同一结构进行多次非线性时程分析，得到结构在每次时程分析中的最大地震响应结果，以强度指标(IM)和损伤指标(DM)作为纵、横坐标，在坐标系内按不同地震动幅值进行描点连线，即将一系列单一的非线性时程分析结果由“点”连成“线”，对比静力pushover曲线形成过程，也称为“动力 pushover曲线”［8-9］，如图1 所示。

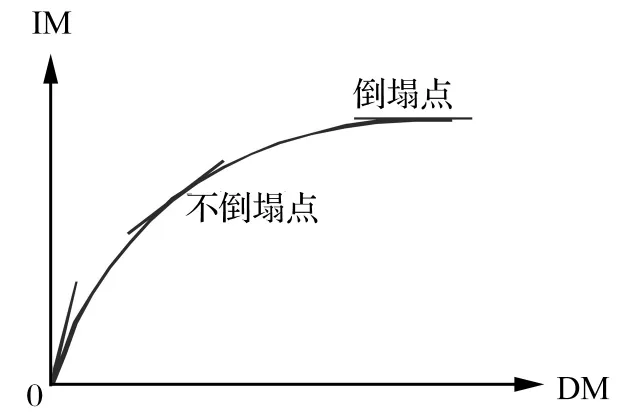
图1 IDA曲线示意图Fig.1 Schematic diagram of IDA curve

常用的损伤指标DM主要包括结构顶层位移、层间位移、损伤指数、最大层间位移角、基底剪力等。在地震反应分析中，常选用最大层间位移角作为DM指标，因为它与节点转动、构件破坏程度和层间倒塌能力直接相关［10］。衡量地震波代表的地面运动强度是动力时程分析中的一个重要问题，不同水准的地面运动强度指标IM表达方式常用的有:地面峰值加速度PGA、峰值速度PGV、地面运动位移峰值PGD，5%阻尼比的结构基本周期对应的加速度谱值Sa(T1，5%)以及结构屈服强度R等。

本文在不同方向下混凝土核心筒抗震性能评估中采用单条地震波的IDA分析方法，即选用一条指定地震记录对结构进行弹塑性动力时程分析，它是以IM指标a1为基础，通过调幅得到不同aλ，并对同一地震波不同调幅的地址记录进行一系列时程分析，将调幅得到的每一级IM值与对应的结构性能参数DM值在二维坐标中绘出，形成一条曲线，即单根IDA曲线。单条IDA曲线中，调幅系数aλ增大表示地震动从弱到强变化，此过程中结构经历了从弹性、弹塑性直至倒塌的过程，可以说，IDA曲线本身具有定性判定结构抗震能力的信息和作用［11］。对于选用 PGA和 θmax作为 IM 和DM指标的IDA分析，计算的终止条件为在PGA和θmax的二维坐标系曲线中，θi和θi+1的连线斜率小于0.2Ke，或者对于混凝土核心筒暂定为θi+1大于等于1/30。定义核心筒在地震作用下的四个性能水平，包括正常使用、暂时使用、生命安全和接近倒塌性能。在IDA曲线上定义核心筒四个性能水平的极限状态判定条件如表1所示。

表1 核心筒四个性能水准对应的曲线斜率下降限值Tab.1 The slope drop limiting values corresponding core walls four performance levels

2 混凝土核心筒算例概况

2.1 计算模型概况

为简化计算，核心筒总层数为20层，各层层高相同，均为4.2 m，总高为84 m，抗震设防烈度为8度，设计基本地震加速度为0.2 g，设计地震分组为第一组，Ⅱ类场地。核心筒恒荷载为3.0 kN/m2(不含楼板自重)，活荷载房间取 2.0 kN/m2，走廊取 2.5 kN/m2。1～3层剪力墙混凝土强度为C40，4～20层为C35，所有楼板混凝土强度均为C35，纵筋为HRB335级，核心筒细节尺寸见楼层平面图所示(图2)。实际中的核心筒不可能单独作为一个结构存在，其水平地震质量受外围框架荷载影响较大，由于整体水平质量和核心筒质量的不确定性较大，本文忽略外围荷载的影响，对单独结果进行分析。模型通过弹塑性分析软件Perform-3d建立，由混凝土剪力墙和连梁单元组成，两种单元均采用较为先进的纤维模型进行模拟［12］。

图2 核心筒平面图Fig.2 Core walls floor plan

2.2 地震波的选择

地震波选用Northridge波的EW分量。混凝土核心筒Y向为第一振型方向，是结构的不利方向，故将结构Y向定为主方向，且两个地震波互相垂直。地震分析工况设置为采用同一个地震记录，对结构地震作用计算依次改变地震作用的输入方向，从+Y向起每次改变15°逆时针旋转变换加载方向，考虑时程分析工作量太大，绕结构1/4圈，找出每个输入方向的地震效应时程最大值和不同输入方向的时程最大值，考察水平地震入射角和竖向地震分量对结构地震反应的影响。在进行混凝土核心筒不同角度地震输入的IDA法评估分析时，本文研究地震输入方向为+Y轴方向逆时针偏45°时的IDA曲线，和上节调幅原则一致，强震记录峰值的加速度固定调幅增量为0.1 g，第一次分析时取PGA=0.05 g，分别调幅为 0，0.05 g，0.10 g，0.20 g，0.30 g，…，1.2 g，1.3 g，1.4 g 共计 15 条地震波，使得调幅范围涵盖从7度小震到9度以上大震的加速度峰值。

3 不同地震输入角度下混凝土核心筒的动力时程分析

3.1 不同地震输入角度的结构响应对比分析

(1)结构位移

Northridge-EW地震波作用下混凝土核心筒的Y向及地震作用角度为沿+Y逆时针15°和45°方向时两个主轴方向的顶点相对水平位移见表2。两种不同角度地震输入的结构顶点位移时程图见图2所示。其中，结构顶点位移取顶部五个节点的平均值。数据表明，结构Y向的最大顶点水平相对位移值单向地震输入大于多向输入，最大值均发生在节点3位置，由于地震波X向分量的作用，核心筒X向多向输入水平最大位移值远大于单向Y轴输入的，表明在大震作用下，多向输入对结构X向的位移影响很大。并可得知相同地震强度、斜向地震作用下，核心筒沿地震输入方向变形更大，剪力墙转角或T形交接处在X和Y两个主轴方向都具有较大变形，使得核心筒空间受力特征加大，这和试验情况相符，故应在转角或T形墙的暗柱设计中注重暗柱尺寸及箍筋配置，使转角剪力墙具有足够保证的延性变形。

(2)结构水平相对加速度

在不同输入角度地震作用下的混凝土核心筒顶层最大水平相对加速度见表3。图3所示为Y向及45°地震输入的结构顶点相对加速度时程曲线。由表中数据可知，在0.4 g峰值加速度下，斜向地震和Y向地震输入下Y向结构的顶层最大水平相对加速度平均值分别为 -0.68 g、-0.54 g 和 -0.65 g，但斜向输入时 X 向加速度较大，合力方向加速度值更大，表明结构总的地震作用有较大幅度提高。

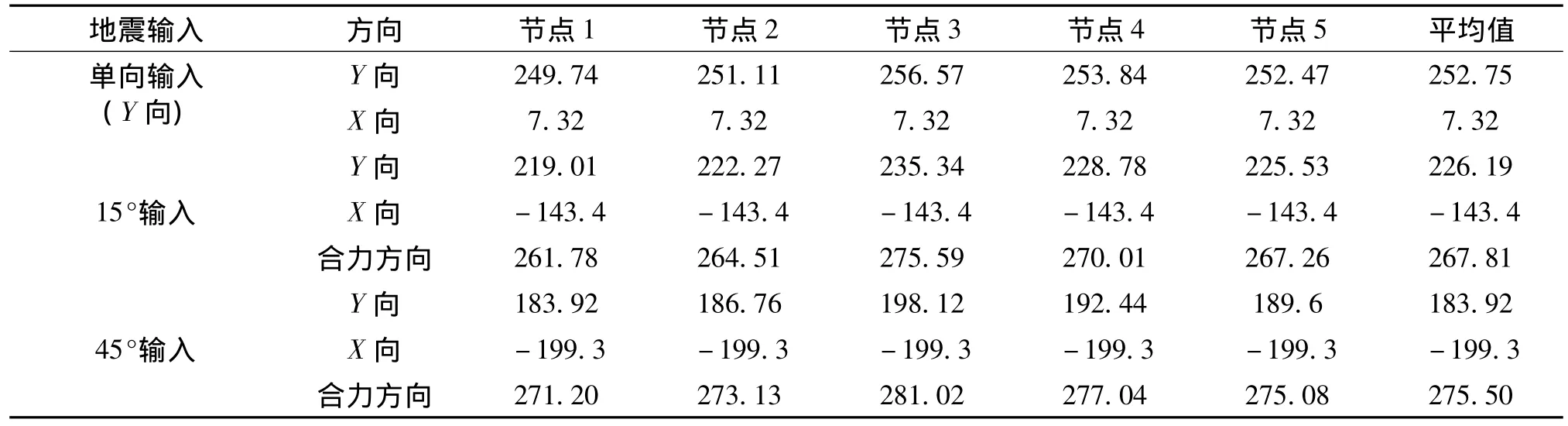
表2 不同地震输入方向结构顶点最大水平位移/mmTab.2 Top maximum horizontal displacements under different directions earthquake actions/mm

表3 不同地震输入方向结构顶点最大水平相对加速度/g Tab.3 Top maximum horizontal accelerations under different directions earthquake actions/g

图2 单向及斜向地震输入的结构顶点相对位移时程曲线Fig.2 Top relative displacement time history curves under unidirectional and oblique directional earthquake actions

图3 单向及斜向45°地震输入的结构顶点相对加速度时程曲线Fig.3 Top relative accelerations time history curves under unidirectional and 45°directional earthquake actions

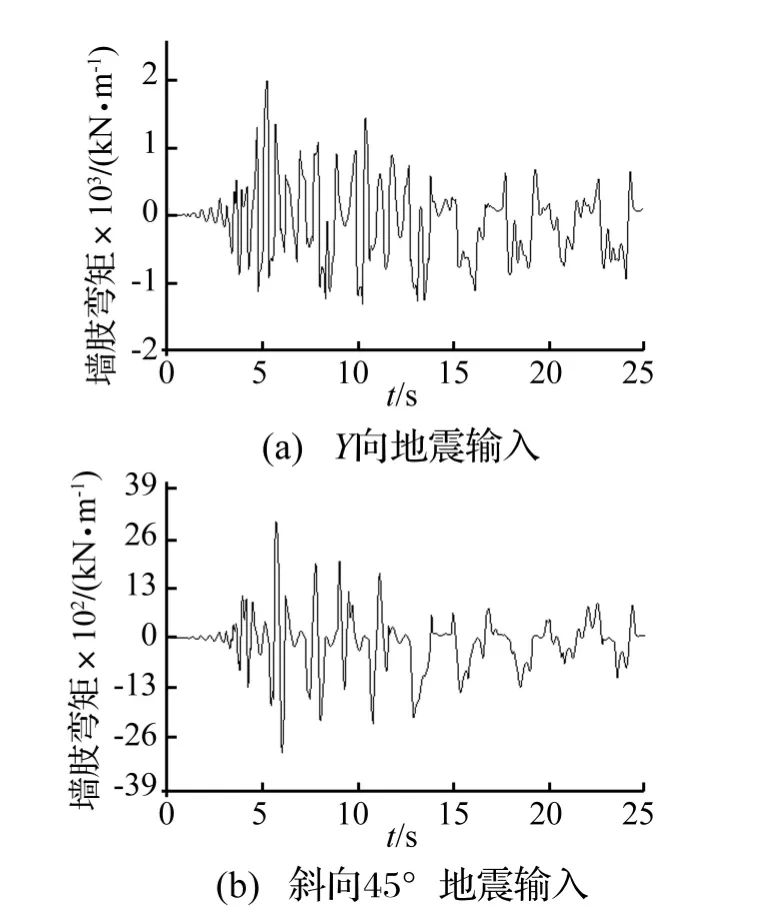
图4 Y向及斜向45°地震输入的结构底部墙肢弯矩时程曲线Fig.4 Bottom shear walls bending moments time history curves under unidirectional and 45°directional earthquake

(3)典型构件内力对比

图4和图5分别为混凝土核心筒在Y向和45°地震作用下的底层墙肢弯矩和轴力时程曲线。从图中可以看出，沿+Y逆时针45°方向地震作用下的同一片底层墙肢无论是平面内弯矩还是轴力均有大幅提高，尤其是对轴力的影响，最大提高了2.9倍，从而导致结构竖向外力增大，结构容易发生因竖向承载力不够而导致的局部损坏或加大P-Δ效应而增大整体倒塌的概率。不同输入角度地震作用下，底层墙肢最大轴力发生在地震输入角度为45°时。在进行结构非线性分析时，结构的P-Δ效应虽然可以予以考虑，但实际中结构受轴力影响非常大，故在设计中应重视这种轴力增大的原因。在进行结构设计时，大震作用下，多维地震作用下的内力要明显偏大，仅考虑单向输入的水平加速度的设计结果会偏于不安全。

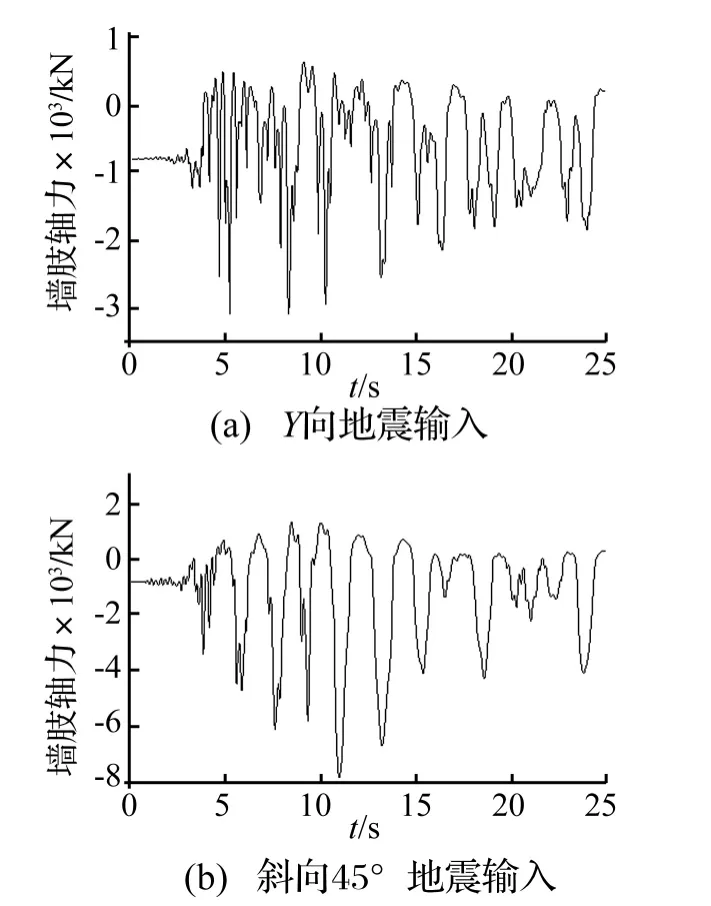
图5 Y向及斜向45°地震输入的结构底部墙肢轴力时程曲线Fig.5 Bottom shear walls bending axial forces time history curves under unidirectional and 45°directional earthquake

图6 不同角度与Y向地震作用效应比值沿楼层分布图Fig.6 The seismic action effects of different angles and Y-axis ratios

图6为核心筒各构件不同输入角度的地震各作用效应与单向地震Y向作用效应比值(XY/Y)沿楼层分布图。从图中可以看出，斜向地震各作用效应与单向地震Y向作用效应比值在剪力墙中的不同内力形式沿楼层的分布关系相差较大，斜向地震输入在同一片墙体中引起的内力更大，外墙轴力影响在8～10层以后逐渐降低，而弯矩则在底层影响最大，其余各层维持在比值为1.2左右。除个别布置的构件出现斜向地震输入下墙体弯矩略微减小的现象以外，其余外墙的XY/Y比值均大于1.0，外部剪力墙在斜向地震作用下轴力和弯矩作用效应增大明显，其中轴力最大增大系数达到了2.9。从图6(a)中可以看出，15°地震输入时，轴力增大系数最小，而45°时最大，规律性较好。剪力墙XY/Y内力比值的增大也反映了对于混凝土核心筒设计时仅考虑单向地震作用是偏不安全的。

3.2 不同地震输入角度及不同地震强度下的结构损伤对比

图7所示为不同输入角度下的核心筒地震作用损伤对比情况，图中角度为与Y轴正方向逆时针方向偏移角度，观察核心筒在不同地震输入角度时，连梁和剪力墙混凝土纤维的损伤发展情况。其中，蓝色代表0.4倍的100%混凝土纤维强度标准值的应变，绿色代表0.6倍强度标准值对应应变值。

从图中可以看出，不同输入角度的地震作用下核心筒最终损伤有较大不同;在同一地震强度下，随着加载角度的增大，剪力墙损伤较Y向地震作用时要明显加重，且主要由X轴一侧墙体向Y侧墙体转移，45°和60°方向时，整体损伤分布最为广泛。0°～15°输入时，核心筒中部剪力墙损伤严重，而大于30°时，损伤主要集中在一个侧面，表明0°～15°范围时，高阶影响较为明显，而大于30°时，主要以第一振型为主。此外，还对核心筒模型进行了Tabas地震波作用下的地震损伤过程进行了分析。结果显示，Y向输入时，Northridge EW地震波作用下的核心筒构件损伤与Tabas地震波作用下损伤顺序不尽相同，Tabas波作用下，剪力墙损伤主要集中在核心筒底部，而在Northridge波作用下，剪力墙损伤除了底部以外，结构中部钢筋也受拉屈服，这主要是因为在不同地震波作用下，结构整体变形相差较大造成，在Tabas波作用下，结构主要以第一振型振动为主，为在Northridge波作用下，结构还以第4振型振动。可见，在核心筒分析中，高阶振型的影响是很大的，不可忽视。

图7 不同输入角度地震作用下核心筒损伤发展对比Fig.7 Core walls damage developments under different directions earthquake actions

3.3 与Y轴45°地震输入的IDA曲线结果分析

选取Northridge-EW地震记录对核心筒进行增量动力弹塑性时程分析，仅取与Y向夹角45°输入的IDA曲线进行研究。对每次调幅后的地震波输入进行结构的时程分析，直到θmax趋向无穷大或达到0.03，此时所得点的连线即为Northridge-EW地震记录下的单条IDA曲线。经过加速度调幅进行了15次动力时程分析，得到15个有用的(PGA，θmax)点，形成 Northridge-EW地震记录较为完整的IDA曲线，如图8所示。

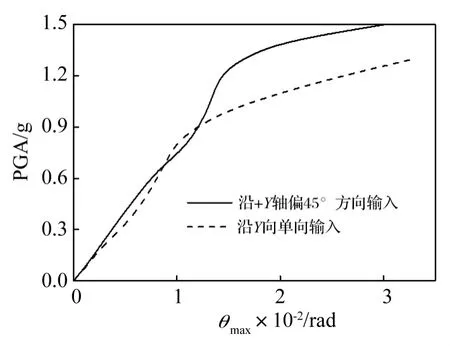
图8 Northridge-EW地震记录的单条IDA曲线Fig.8 Northridge-EW seismic-record IDA curves

从IDA曲线看，沿45°输入的斜向地震动对混凝土结构IDA曲线影响较大，两条IDA曲线在PGA为0.2 g以前几乎重合，但之后出现分离，但相差还不大，在PGA=0.9 g以后，两条曲线出现较大分离，Y向输入层间位移角随PGA增大而变化加快。从损伤情况看，斜向输入时在同一层间位移角下墙体破坏和单向输入时有较大不同。这样，斜向地震输入单条IDA曲线上混凝土核心筒四个性能点对应的量化位移指标与单向单条地震输入的也有所不同。对于Northridge-EW地震记录，按照给出的不同性能水准与IDA曲线斜率下降幅度的关系，参照表1的具体判别标准对图8所示单条IDA曲线进行分析，与Y轴斜向45°地震输入分析结果为:PGA=0.05 g时结构达到正常使用性能点，此时θmax=1/1284;PGA=0.25 g时达到暂时使用性能点，此时θmax=1/335;PGA=0.7 g时达到生命安全性能点，此时θmax=1/109;PGA=1.30 g时达到接近倒塌性能点，此时θmax=1/63，这和文献［13］中Y向输入各性能点位移角限值相差不大。由此可知，虽然单个构件在斜向荷载作用下产生的内力较大，但由于整体结构直接参与地震作用的构件数量增多，即X、Y方向构件均参与抗震，最终各性能点对应的量化指标与单向地震输入时对比相差并不明显。本文仅采用单条地震记录进行斜向地震输入，可能与多条地震记录IDA曲线及结果产生偏差。

4 结论

(1)通过不同方向地震作用与单向地震作用下混凝土核心筒的地震效应对比可知，在进行结构设计时，大震作用下，斜向地震作用下的内力要明显偏大，仅考虑单向输入的水平加速度的设计结果会偏于不安全。

(2)斜向地震作用下外墙的弯矩和轴力均有大幅提高;核心筒变形和加速度随加载角度的增加而变化，其中最大响应值对应角度约为45°。斜向地震作用下，同一地震强度，结构损伤较单向地震作用时有明显不同，随着加载角度的增大，剪力墙损伤较Y向地震作用时要明显加重。

(3)斜向地震输入对混凝土结构IDA曲线有一定影响，但各性能点对应的量化位移指标与Y向单条地震输入时相差不大。

［1］尧国皇，王卫华，郭 明.超高层钢框架-钢筋混凝土核心筒结构弹塑性时程分析［J］.振动与冲击，2012，31(14):137-142.

YAO Guo-huang，WANG Wei-hua，GUO Ming.Response of tall-building steelstructureto multi-dimensionalseismic action［J］.Journal of Vibration and Shock，2012，31(14):137-142.

［2］郭伟亮，滕 军，容柏生，等.高层斜交网格筒-核心筒结构抗震性能分析［J］.振动与冲击，2011，30(4):150-155.

GUO Wei-liang，TENG Jun，RONG Bai-sheng，et al.A seismic behaviour of a diagrid tube-core tube structure ［J］.Journal of Vibration and Shock，2011，30(4):150-155.

［3］易方民，高小旺，张维嶽，等.高层建筑钢结构在多维地震动输入作用下的反应［J］.建筑结构学报，2003，24(3):33-43.

YI Fang-min，GAO Xiao-wang，ZHANG Wei-yue，et al.Response of tall-building steel structure to multi-dimensional seismic action［J］.Journal of Building Structures，2003，24(3):33-43.

［4］曹万林，王光远，吴建有，等.不同方向周期反复荷载作用下L形柱的性能［J］.地震工程与工程振动，1995，15(1):67-72.

CAO Wan-lin，WANG Guang-yuan，WU Jian-you，et al.Behavior of“L”shape column under different directional cyclic loading［J］.Earthquake Engineering and Engineering Vibration，1995，15(1):67-72.

［5］黄选明，张建伟，曹万林，等.钢筋混凝土非工程轴方向受力短肢剪力墙抗震性能试验［J］.北京工业大学学报，2010，36(2):172-178.

HUANG Xuan-ming，ZHANG Jian-wei，CAO Wan-lin，et al.Seismic performance of short pier RC shear wall without engineering axial force［J］.Journal of Beijing University of technology，2010，36(2):172-178.

［6］管民生，王险峰，杜宏彪，等.框架-剪力墙结构单双向地震输入下的反应分析［J］.广东工业大学学报，2010，27(2):17-20.

GUAN Min-sheng，WANG Xian-feng，DU Hong-biao，et al.The Seismic response analysis of frame-shear wall structures under uni-and bi-directional seismic excitation［J］.Journal of Guangdong University of Technology，2010，27(2):17-20.

［7］Bertero V V.Strength and deformation capacities of buildings under extreme environments［M］.Prentice-Hall:Englewood Cliffs，NJ，Structural Engineering and Structural Mechanics，Pister KS(ed.)，1977:211-255.

［8］Vamvatsikos D，Cornell C A.Incremental dynamic analysis［J］.Earthquake Engng Struct.Dyn.，2002，31(3):491-514.

［9］ Vamvatsikos D，Cornell C A.Applied Incremental dynamic analysis［J］.Earthquake Spectra，2004，20(2):523-553.

［10］玉 军.钢筋混凝土高层建筑结构抗震弹塑性分析方法的研究及其应用［D］.长沙:湖南大学，2007.

［11］王秋维，史庆轩，侯 炜，等.型钢混凝土框架结构基于增量动力分析的抗震性能评估［J］.世界地震工程，2011，27(1):34-40.

WANG Qiu-wei，SHI Qing-xuan，HOU Wei，et al.Seismic performance evaluation of SRC frame structures based on incrementaldynamic analysis［J］. World Earthquake Engineering，2011，27(1):34-40.

［12］ Perform Components and Elements，CSI，2006.

［13］史庆轩，侯 炜，田 园，等.钢筋混凝土核心筒性态水平及性能指标限值研究［J］.地震工程与工程振动，2011，31(6):88-95.

SHI Qing-xuan，HOU Wei，TIAN Yuan，et al.Study on seismic performance levels and performance index limit values of reinforced concrete core wallstructure［J］. Earthquake Engineering and Engineering Vibration，2011，31(6):88-95.