基于加速度响应相关性的结构损伤识别方法

闫维明，顾大鹏，陈彦江，杨小森

(1.北京工业大学 工程抗震与结构诊治北京市重点实验室，北京 100124;2.甘肃省交通规划勘察设计院有限责任公司，兰州 730030)

损伤识别技术是结构健康监测系统的关键所在，也是结构健康监测领域具有挑战性的研究课题［1］。由于土木工程结构的复杂性，损伤分布和损伤程度有很大的随机性，损伤识别方法在实际工程应用中遇到了很多困难，比如测量噪声干扰、测量数据不完整、环境条件复杂多变、模型误差、识别方法不完善、局部损伤的不敏感性等。基于振动信号统计特征的结构损伤识别方法，是从统计意义上构造损伤因子，因此可以降低识别过程中的不确定性，包括噪声的影响等。李忠献等［2］采用位移响应的方差作为损伤因子，利用神经网络技术对悬臂梁进行了损伤实验分析。文献［3］则以位移响应的4阶统计矩作为损伤因子，通过优化算法进行损伤的识别。文献［4］指出统计矩指标实际上是结构响应信号能量的函数，并将该指标用于剪切型框架结构的损伤识别中，取得了很好的效果。杨小森［5］提出不同测点的位移响应联系强弱取决于测点间结构刚度的大小，并通过有限元验证了结论的正确性。

而实际应用中往往是用加速度传感器测量加速度，位移传感器测量位移［6］，因而本文在文献［5］的基础上，提出以测点加速度响应相关特性为损伤因子，采用神经网络方法识别结构损伤位置和程度，并通过试验验证了该方法的适用性。

1 加速度响应的统计特征分析

为推导出结构测点加速度的相关特性，根据结构随机振动理论［7］，结构振动的激励和响应可以看作为一个随机过程，则结构振动时的公式如下:

式中:M、C和K分别为结构的质量、阻尼和刚度矩阵;x(t)是位移;f(t)为结构的激励向量。其中，结构的位移可以写成:

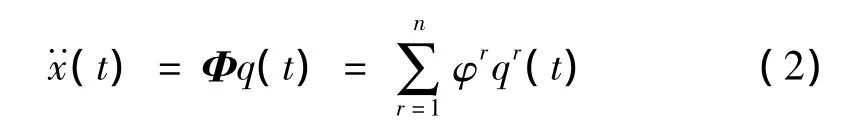
式中:Φ为结构的模态矩阵;q(t)为自振模态的广义坐标向量;qr(t)为第r阶模态的广义坐标;φr为第r阶自振模态。

如果M、C和K是正交阵，则将式(2)代入式(1)可同时左乘:

式中:ωnr为第i阶模态无阻尼频率;ξr为第i阶模态阻尼;mr为第i阶模态质量。

利用杜哈米积分［8］(Duhamel Integration)可以得到:

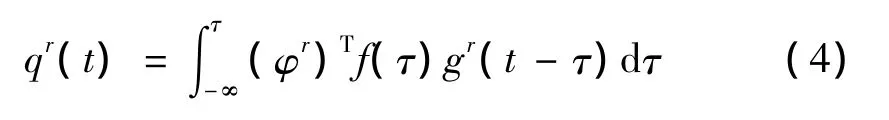
可以得到，结构中k点有脉冲激励时，i点的响应为:

根据卷积的微分性质［9］，结构的加速度响应可以求得:

如果fk(t)为脉冲激励时，系统的加速度脉冲响应函数为:

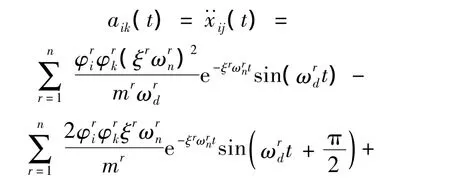
在环境振动下结构的位移响应的互相关函数:

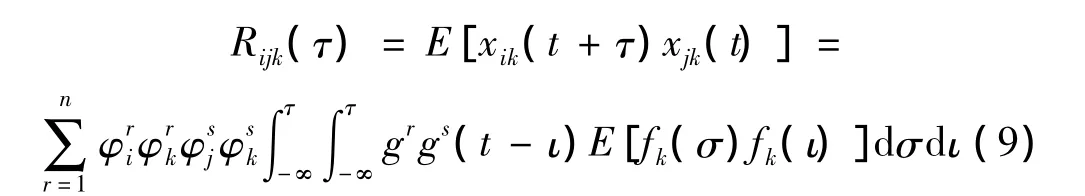
如果激励为白噪声，则激励的互相关函数可以表示成为:

式中:αk为一个常数，δ(ι-σ)是 Dirac函数。

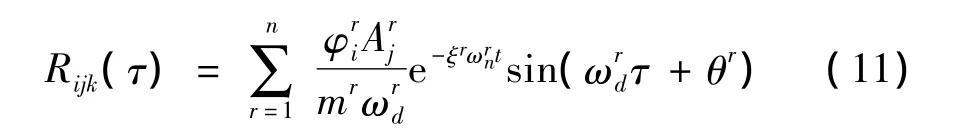
从式(11)中可以推导出，结构位移响应的相关函数与结构的振动模态参数相关。进一步根据均方导数的性质［10］，通过式(11)推导出速度的相关函数为:

通过式(12)推导出加速度的相关函数为:

进而可以推出，白噪声激励下加速度响应的协方差为:

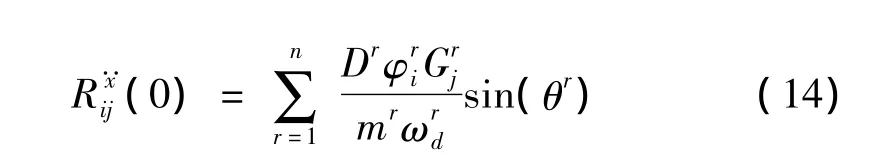
式中:为与刚度相关的常数，θr为初相位。Dr为与模态阻尼和频率相关的常数。

因此白噪声激励下，加速度响应的回归系数lxi，xj为:

由式(15)可以看出，测点加速度响应的回归系数是结构振动模态和结构刚度的函数，即加速度响应的回归系数与结构损伤的位置和程度是相关的。因此，可以将结构测点加速度响应的相关特性作为损伤识别的指标。为了得到更好识别效果，构造合理识别指标是最重要的［11］，对于相关性分析，参考点的恰当选择是非常重要的［12］。对加速度响应的相关特性进行归一化处理，构造损伤参数统计特性变化率R:

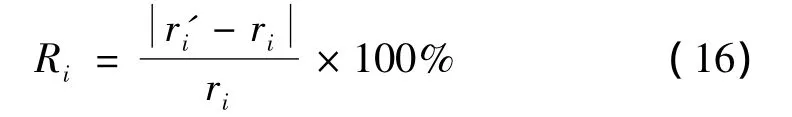
式中:ri'表示损伤后结构i点相对参考点的加速度回归系数;ri表示完好状态下结构i点相对参考点的加速度回归系数。

2 数值模拟

为验证本文提出的利用测点加速度响应相关特性作为损伤因子的正确性，对混凝土简支梁进行有限元数值模拟。简支梁梁长4.0 m，横截面为矩形截面，高度为0.3 m、宽度为0.15 m，具体结构形式如图1所示(单位:cm)。材料弹性模量为3.0×104MPa，质量密度为2 500 kg/m3，泊松比为0.15。完好状态时结构阻尼为0.02。参考已有的文章结论，认为混凝土结构在损伤时结构的阻尼增加［13］，有限元在结构损伤后将结构阻尼增加0.03，模型在构造损伤采用文献［14］所述的弹性铰方法，弹性铰刚度K采用文献［15］计算方法求得。

简支梁模型共划分有20个单元，21个结点，有限元模拟中简支梁具体划分情况见图1，图2为有限元模拟中采用的白噪声激励和功率谱。激励采用基底输入。

图1 简支梁有限元模型(单位:cm)Fig.1 Simple support beam model

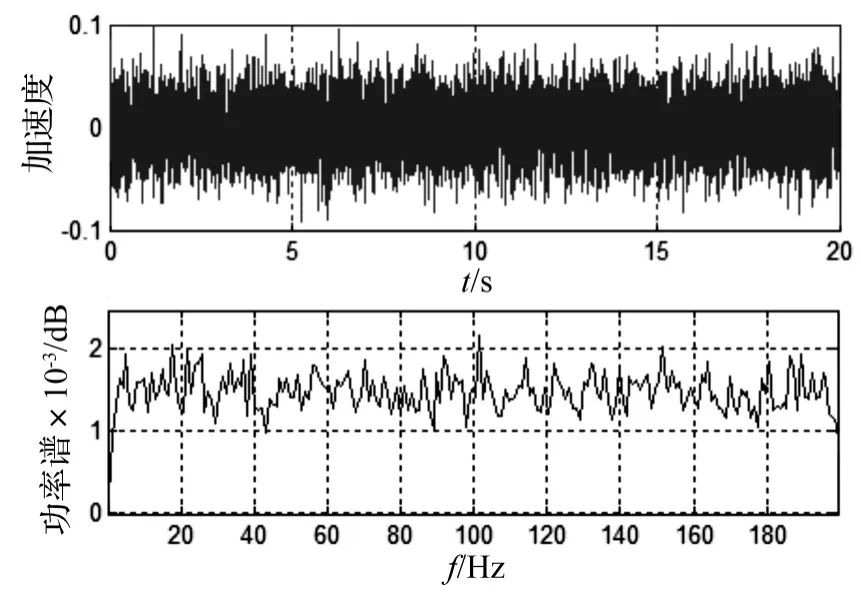
图2 白噪声的时程曲线和功率谱Fig.2 Power spectrum＆ time histories of white noise excitation

有限元模拟中对简支梁较容易损坏的跨中部分单元进行不同程度的损伤模拟。文献［12］中提到参考点分析时，参考点应当与测点有较高的相关性，因而模拟和试验均以跨中节点作为参考点，并利用公式16分别计算不同损伤程度下结构加速度的损伤因子值。图3为跨中10、11、12单元损伤10%～40%时简支梁各节点损伤因子的计算结果。从图中可以看出，损伤单元处损伤因子图形明显发生畸变，基于加速度响应相关性的损伤因子能反应损伤程度，并随着损伤程度的增加，损伤因子整体呈增长的趋势。

3 基于神经网络的损伤识别

利用上一节证明的损伤因子，对简支梁进行损伤程度和损伤位置的识别。采用的方法是具有强大的非线性建模能力、容错性和鲁棒性的BP神经网络［16］，且在国内外已经取得了很多研究成果［17-18］，计算方法为LM算法。

通过有限元模拟的建立样本库，为减少样本的数量根据结构形式的特点，主要建立1/4跨到3/4跨之间的损伤样本，损伤等级分3级10%、20%和30%，分别计算15个单侧单损伤样本、15个对称多损伤样本，之后用其中的3组数据验证训练起来的样本库，利用结构的对称性建立15组单损伤样本。图4和图5为结构在单损伤和对称多损伤程度30%状态下样本库。

图4 单损伤样本Fig.4 Single-damage sample

利用建立的神经网络，对一离散多损伤样本和一个连续多损伤样本进行识别，识别结果列于表1和表2，可以看出经过多次训练后的样本识别精度高，能够准确的识别出结构的损伤位置和损伤程度。

4 实验验证

为了验证本文所提出的基于结构加速度响应统计特征的神经网络损伤识别方法，用一根混凝土简支梁模型进行结构损伤模拟实验。梁长4.0 m，计算跨径为3.6 m，梁横截面为矩形，截面高 0.3 m、宽 0.15 m，如图6所示。混凝土简支梁用C30混凝土和HRRB335钢筋建成。对混凝土梁进行了6级静力加载，模拟不同程度的损伤，试验照片见图7，加载曲线和各级的刚度见图8和表3。5#传感器的加速度响应时程曲线如图9所示。

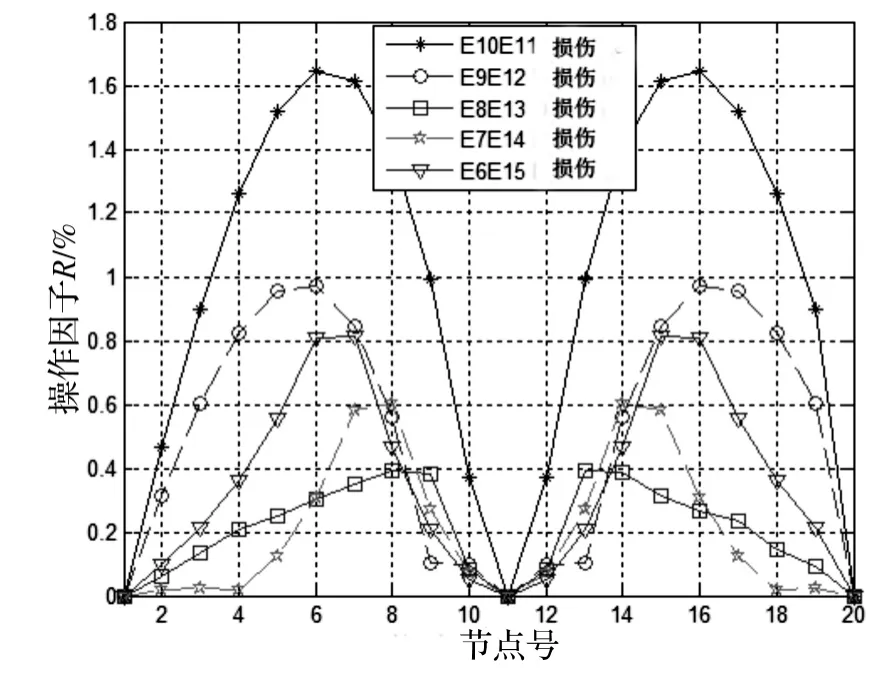
图5 对称损伤样本Fig.5 Multi-damage sample

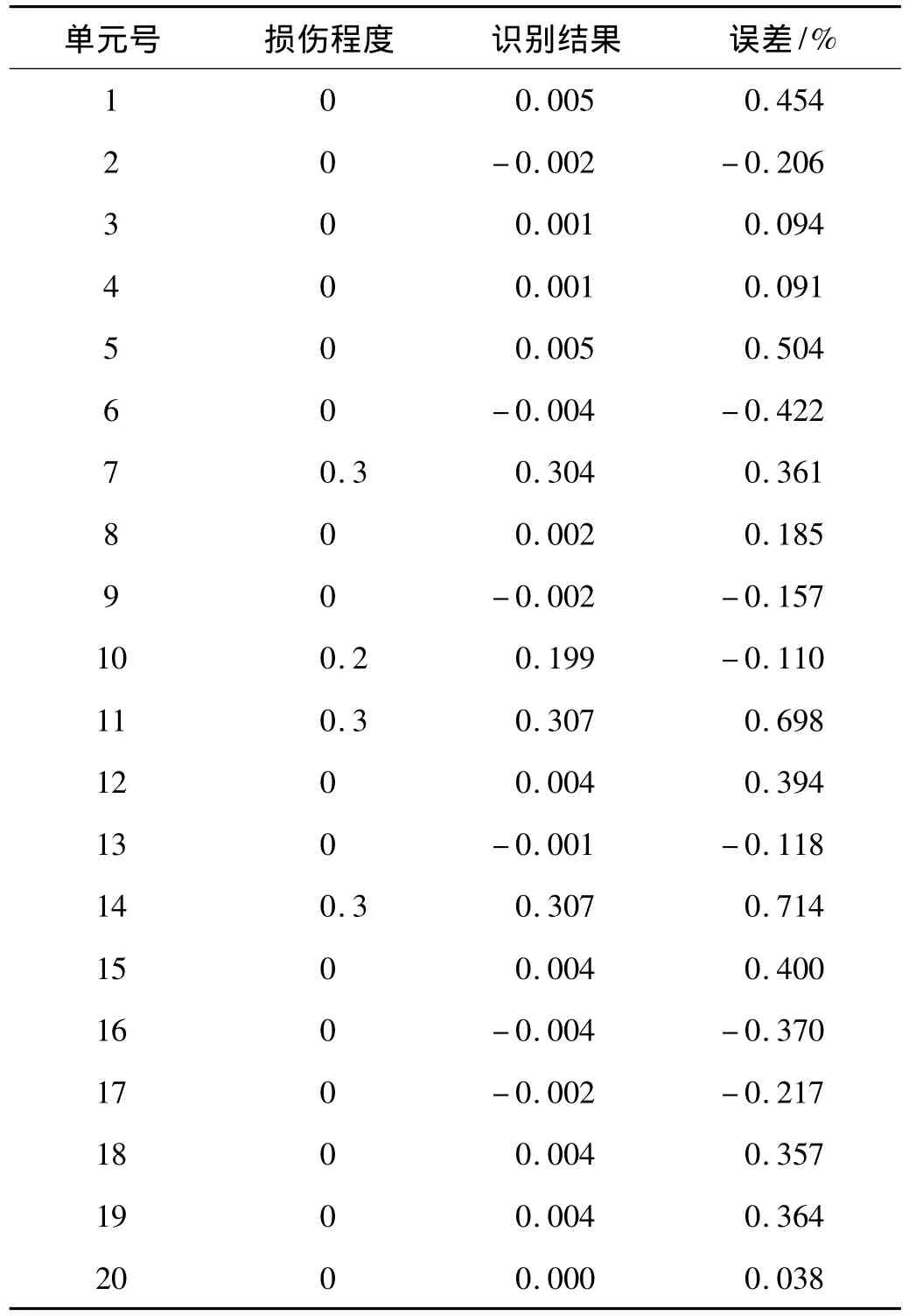
表1 多损伤识别结果Tab.1 Results of the damage detection

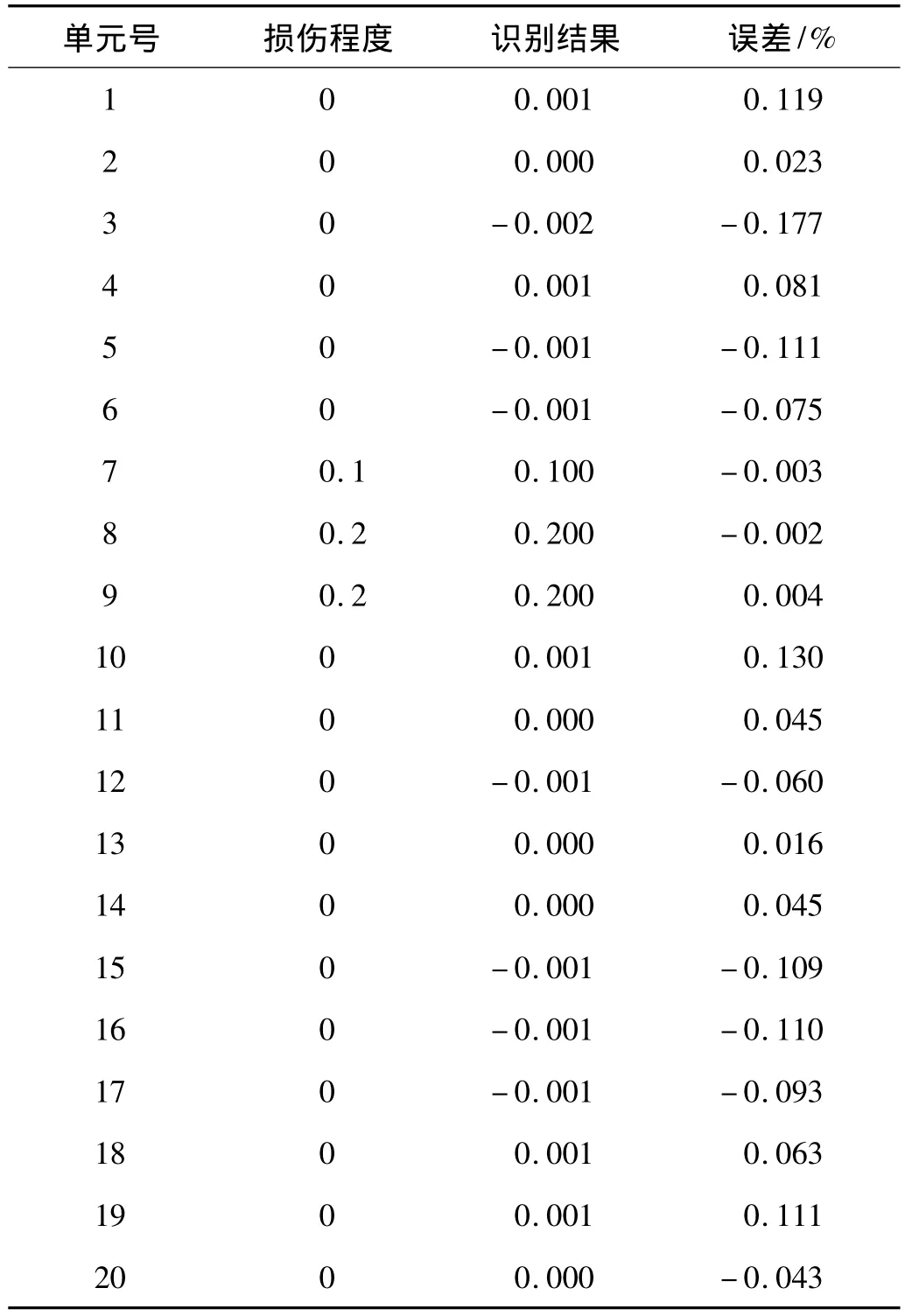
表2 连续多损伤识别结果Tab.2 Results of the damage detection

功率谱曲线如图10所示。对结构进行有限元模拟，建立各点损伤因子的神经网络样本库，反复训练样本库，进行损伤识别。

图6 钢筋混凝土简支梁模型Fig.6 Layout drawing of the reinforced concrete beam

图7 钢筋混凝土简支梁试验照片Fig.7 Pic of the model test

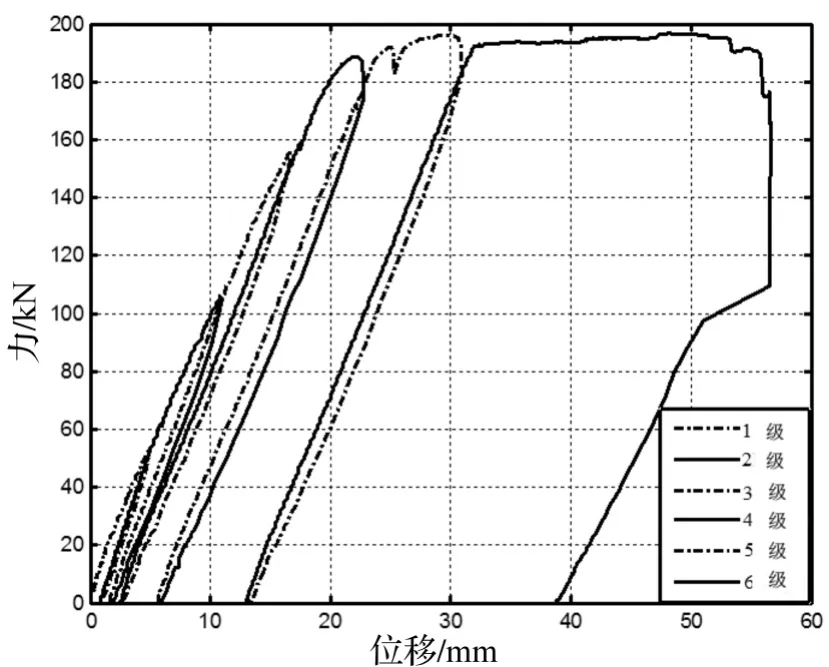
图8 静力加载曲线Fig.8 Force-displacement curve of beam

表3 各级加载刚度变化表Tab.3 Static rigidity and damage

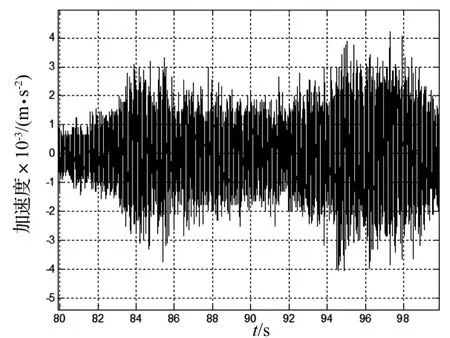
图9 环境激励时程曲线Fig.9 Time histories of white noise excitation

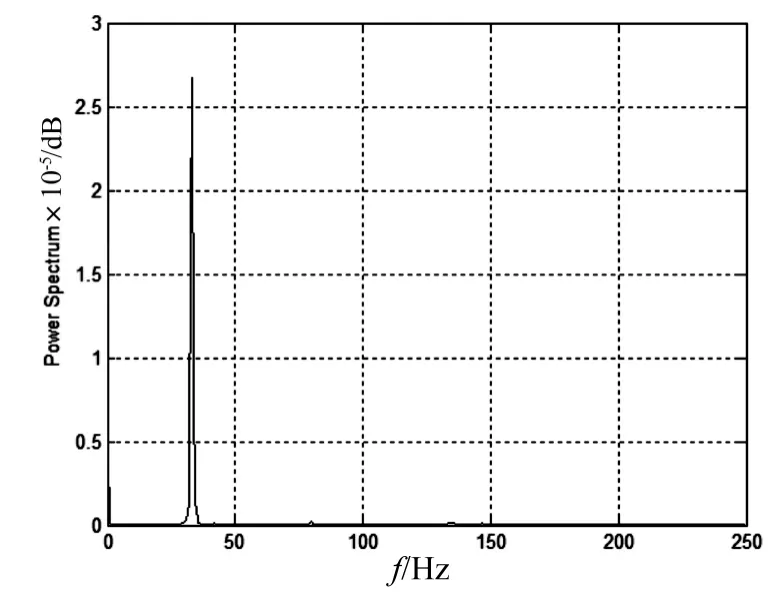
图10 跨中测点功率谱曲线Fig.10 Power spectrum of white noise excitation

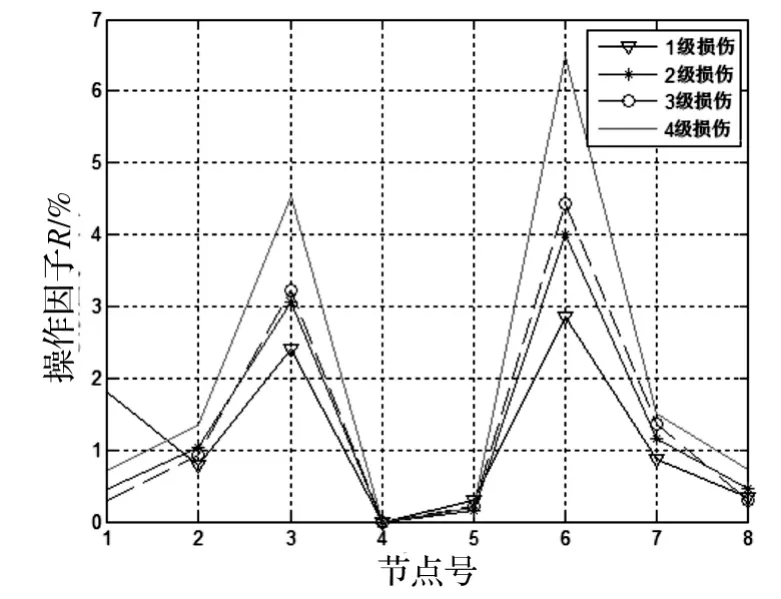
图11 前4级加载后损伤因子图Fig.11 Damage index under damage

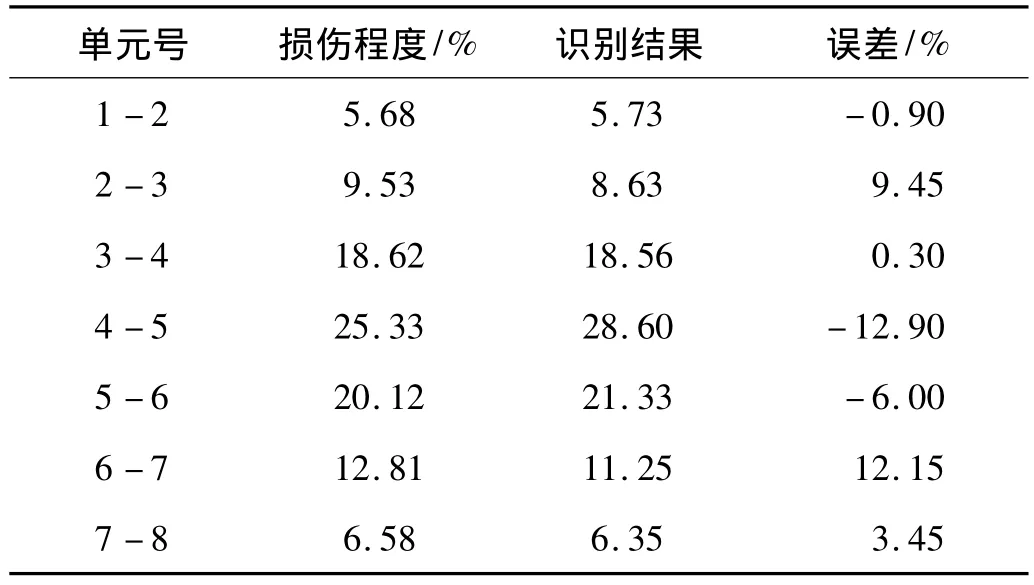
表4 第三级加载后的损伤识别结果Tab.4 Damge detection of 3rd degree

实测混凝土简支梁的损伤因子变化图见图11，根据前面的分析，可以发现在前四级的加载过程中，4、5号传感器间发生损伤，通过反复训练的神经网络可以识别出各级损伤后的简支梁损伤位置，表5为结构在第三级荷载作用下的损伤识别结果，可以看出对于损伤的位置判断较为准确，对于损伤程度识别误差较大。神经网络识别精度依赖神经元的数量，对于工程结构无法穷尽样本库，所以损伤程度误差较大。由此可以得出结论，实验结果进一步证明了本文提出的损伤识别方法的可靠性和有效性。

5 结论

本文提出一种基于结构测点加速度响应的相关特性作为损伤指标的BP神经网络损伤识别方法，并通过对结构测点加速度响应的相关特性与结构模态参数关系的推导、对混凝土简支梁损伤识别过程的数值模拟以及一个混凝土简支梁损伤识别的实验验证三个方面进行研究，得出以下结论:

(1)从理论上证明结构加速度响应的相关特性包含了结构的固有模态信息，能够反映结构的模态参数。其作为损伤指标进行结构损伤识别是可行的。

(2)采用结构节点加速度响应的相关特性作为损伤指标的神经网络方法可以准确识别出梁结构中的损伤位置及损伤程度，从而证明本文所提出的BP神经网络损伤识别方法的可靠性和有效性。

［1］ Pines D J，Aktan A E.Status of structural health monitoring of long-span bridges in the united states［J］.Progress in Structural Engineering and Materials.2002，(4):372-380.

［2］李忠献，杨晓明，丁 阳.基于结构响应统计特征的神经网络损伤识别方法［J］.工程力学，2007，(7):1-7.

LI Zhong-xian，YANG Xiao-ming，DING Yang，Damage identification neural network method based on statistical property of structural responses，Engineering［J］.Mechanics，2007(7):1-7.

［3］陈晓强.基于能量指标的结构损伤识别理论与试验研究［D］.武汉:华中科技大学，2009.

［4］ Zhang J，Xu Y L，Xia Y，et al.A new statistical momentbased structural damage detection method.Structural Engineering and Mechanics，2008，30(4):445-446.

［5］杨小森.大跨度斜拉桥全寿命健康监测几个关键问题研究［D］.北京:北京工业大学，2011.

［6］谷口修.振动工程大全［M］.尹传家译.北京:机械工业出版社，1983.

［7］Clough R W，Penzien J.Dynamics of structures［M］.New York:McGraw-Hill，Inc.，2003.

［8］Crandall S H.Random vibration［M］.New York:John Wiley＆ Sons，Inc.，1958.

［9］王俊芳，王石青，焦青霞.卷积公式的推广［J］.华北水利水电学院学报，2007，(03):110-112.

WANG Jun-fang， WANG Shi-qing， JIAO Qing-xia，Generalization on formula for convolution［J］.Journal of North China Institute of Water Conservancy and Hydroelectric Power，2007，(03):110-112.

［10］欧进萍，王光远.结构随机振动［M］.高等教育出版社，1998.

［11］ Au S K，Beck J L.A new adaptive importance sampling scheme for reliability calculations［J］.Structural Safety，1999，21(2):135-158.

［12］叶锡钧，颜全胜，王卫锋，等.基于多参考点稳定图的斜拉桥模态参数识别［J］.华南理工大学学报，2011，(09):41-49.

YE Xi-jun，YAN Quan-sheng，WANG Weifeng，et al.Modal parameter identification of cable-stayed bridge based on multiple reference dofs stabilization diagram［J］.Journal of South China University of Technology，2011 ，(09):41-49.

［13］王 卓，闫维明，秦栋涛，等.钢混简支梁加载损伤后耗能特征试验研究［J］.振动、测试与诊断，2009，(01):66-71.

WANG Zhuo， YANWei-ming， QIN Dong-tao， etal，Dissipative characteristic investigation of simply-supported reinforced concrete beams with loading damages［J］.Journal of Vibration Measurement＆ Diagnosis，2009，(1):66-71.

［14］ Shen Y P，Tang C T.Effects of cracks on frequency spectra ofvibration ofcantileverbeamsand plates［J］. Acta Mechanica Solida Sinica，1982，(2):247-251.

［15］ Liu H W，Chu E S，Liebowitz H.Cracked columns under compression fixed ends［J］.Engng.Frae.Meeh，1971，(3):219-230.

［16］ Das P K，Zheng Y.Cumulative formation of response surface and Its use in reliability analysis ［J］. Probabilistic Engineering Mechanics，2000，15(3):309-315.

［17］ Kaymaz I，McMahon C A.A response surface method based on weighted regression for structural reliability analysis［J］.Probabilistic Engineering Mechanics，2005，20(1):11-17.

［18］ Elhewy A H，Mesbahi E，Pu Y.Reliability analysis of structures using neural network method［J］.Probabilistic Engineering Mechanics，2006，21(1):44-53.