改善垂直轴风机效率的叶片转动惯量试验研究

吴伟斌 刘思远 李 荣 罗泽欣 陈海聪 罗朝军 洪添胜

(华南农业大学南方农业机械与装备关键技术教育部重点试验室1，广东 广州 510642;国家柑橘产业技术体系机械研究室2，广东 广州 510642;华南农业大学工程学院3，广东 广州 510642)

0 引言

风力发电机的效率是指发电机所发出的功率与风机扫风面积内的风能之比。目前，绝大部分研究都是针对自然风状态下提高发电效率［1－6］。而现实过程中，类似火车行驶、飞机起降所制造的风大多具有风速大、持续时间短的特点。在这种条件下，风机有效工作时间短、发电效率较低。

S型垂直轴风力发电机具有叶片简单、抗风能力强等特点［1－6］。Ushiyama等学者对S型风机进行了大量的理论和试验研究，分析了结构参数对风机效率的影响［7－12］。事实上，由于应用场合不同，单纯从理论上分析难以真实地反映风机性能的变化［13－15］。

本文对S型垂直轴风机进行了改进，在风机叶片边沿上采用加厚型设计(作为一种配重)，从而增加风机的转动惯量，使风机在停风后的转动时间延长，最终提高了风机的效率。

1 研究方法

1.1 设计方案

本文通过利用试验室的大功率工业风扇模拟自然风，测试具有不同叶片质量的风能发电机的输出电压。利用虚拟仪器LabVIEW平台，实现风机输出电压信号采集处理系统的构建，并据此得出不同叶片的转动惯量对风能发电机发电效率的影响。试验设计方案如图1所示。

图1 试验设计方案示意图Fig.1 Block diagram of experiment scheme

1.2 试验理论基础

风力发电机是将风能先转换成风机叶片的动能，再转换成电能的装置。在风机的叶片上安装配重，可以起到增加转动惯量的作用。

风机绕z轴转动时，角速度为ω、转动惯量为J、质点mi到主轴的垂直距离为ri，则任一点mi的速度为vi=riω，于是风机的动能为:

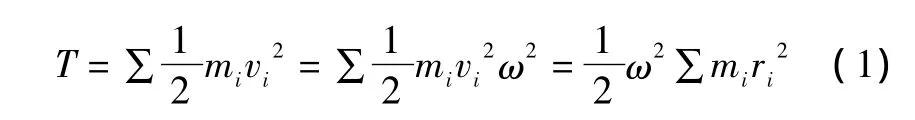
式中:∑mi为对风力发电机所有点的转动惯量的积分，其值等于J。

理论分析表明，在同样的风源条件下，提高风机的转动惯量可以增加风机的动能，同时延长风机的发电时间，进而提高风机的效率。

1.3 风机发电效率的计算

风机发电效率的计算公式为:

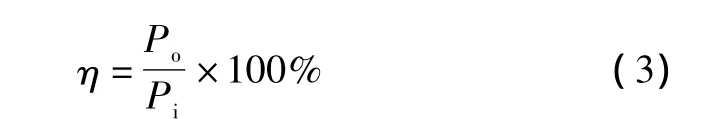
①风机的输入功率

当空气流吹过风轮扫面A时，其质量流量为ρvA，每秒所携带的能量为:

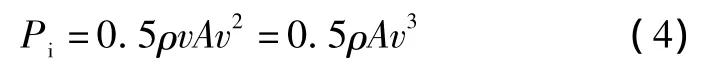
式中:ρ为空气密度，kg/m3，通常因风速较低而视为不可压缩流体;v为风速，m/s;A为旋转直径D与高度H的乘积。

②风机的输出功率

风能发电为间断发电，实际应用中一般将风机所发的电存储到蓄电池再使用，这个过程中须经过整流、滤波、升压、稳压等过程，电能转换效率进一步下降。风机输出功率测量方案示意图如图2所示。

图2 风机输出功率测量示意图Fig.2 Schematic diagram of the measurement of output power of wind turbine

试验时，采用负载箱等效设计了一个回路，用来代替充电电路，这样输出功率的计算大大简化。风机输出功率的计算公式为:

式中:R为负载的电阻值;U为负载两端的电压;I为流过负载的电流大小;φ为电压与电流的功率因素角。

1.4 测试对象

①风力发电机的选用

试验所测试的风机是一种S型垂直轴双层叶片结构的风力发电机，其型号为JDX，输出为三相交流电，额定输出电压为交流三相12 V，最大输出功率为200 W。

②配重的设计

通过设计同样规格、不同厚度的不锈钢板作为配重，实现对风机叶片转动惯量的参数化改变。不锈钢板的 GB牌号为0Cr18Ni9，规格为30 mm×300 mm(钢片的长度与风机叶片的长度相同，形状相似)。预试验发现:当钢板厚度超过8 mm时，风机启动风速由2 m/s提高至4.2 m/s，对实际应用不利，故在1～7 mm中选择配重，最终选定了2 mm、6 mm两种规格。

配重的安装过程为:将同一厚度的钢片安装在风机各个叶片背面，在最大程度上与叶片形成黏合状态，这样可以减小旋转时空气阻力的影响。

③风源的设计

采用大功率工业风扇代替风源。本试验选用型号为FS 75工业风扇、额定电压220 V、额定功率290 W。利用工业风扇上的三档调速器，使得风速分别为12.7 m/s、11.6 m/s、9.80 m/s。

④负载的设计

试验过程中，采用便携式AE200电子负载箱。现实应用中，只有当风机输出电压大于4 V，电能才能有效利用。预试验发现，采用电阻箱时，由于风机线圈绕组存在内阻，当电阻箱阻值大于80 Ω时，输出电压才能有效利用;而当电阻箱取值大于500 Ω时，效率低于35%，风机的输出效率会下降，不符合实际应用情况。因此，试验中阻值取为 100 Ω、200 Ω、360 Ω。

1.5 软件界面

①软件设计整体结构

主程序流程如图3所示。

图3 主程序流程图Fig.3 Flowchart of the main program

基于LabVIEW2010平台，结合多功能数据采集卡DAQCard-6024E设计了S型结构风力发电机。它主要完成对转速测量传感器计数以及输出电压信号采集、处理、分析和数据保存及显示等工作。

②操作界面

软件操作界面分为试验参数设定和实时数据显示、实时波形图显示两部分。

通过设定采样频率、配重的厚度以及负载的大小，便可以计算出瞬时电压、瞬时功率、转速和角加速度。该界面不仅可以实时显示电压、功率、转速;而且它也可以将数据存储下来，为后期数据处理使用。

2 正交试验设计与结果分析

2.1 系统正交试验设计

①试验因素水平表的确定

转动惯量是本次试验主要考察的因素，风力和负载的大小对求解发电效率会有较大的影响。正交试验水平因素设计如表1所示。

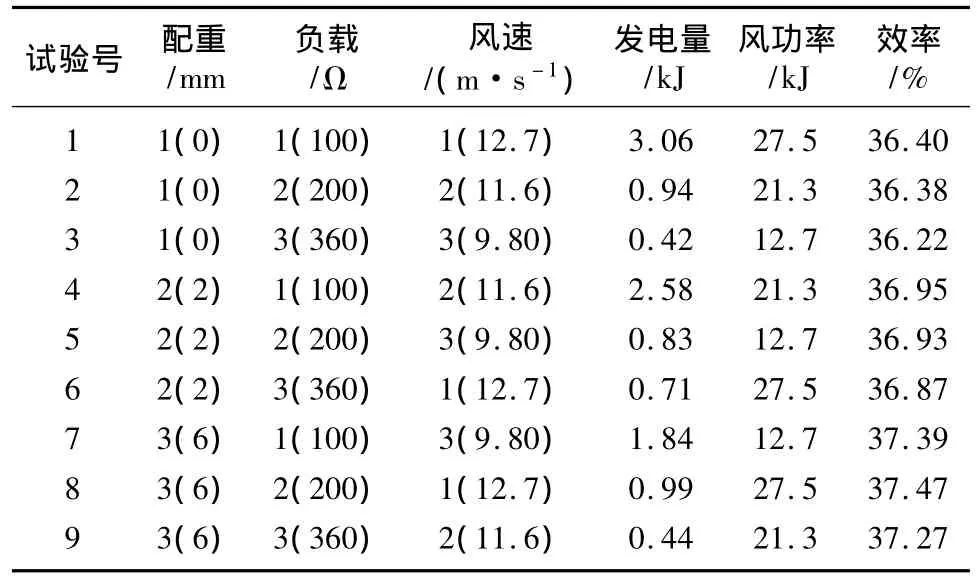
表1 正交试验水平因素表Tab.1 Level factors of orthogonal experiment

②试验步骤

step 1:按照试验原理图搭接好电路，3台工业风扇相互成60°夹角摆开(风扇由一个开关同时控制)，风机置其前方20 cm处。

step 2:按照正交试验水平因素表，利用万用表以及数显式风速仪调节负载箱负载和工业风扇的档位。

step 3:启动LabVIEW平台和工业风扇，2 min后停止工业风扇;待风机输出电压为0时，关闭LabVIEW平台，将数据导出，记下试验指标即发电量。

step 4:根据表1重复step 2，并填写试验表格;然后根据风力大小，求解风功率和风机效率。

③正交试验结果的方差分析

以各次试验的发电效率作为指标，运用SPSS软件对转动惯量对风机发电效率的影响的正交试验进行方差分析。分析表明:配重对风机发电效率的影响极显著、负载对风机发电效率影响显著、风速对风机发电效率影响的影响不显著。风机发电效率与转动惯量、负载和风源对电压信号采集的影响作用逐渐减小。

④正交试验结果的方差分析

正交试验数据极差分析结果如图4所示。

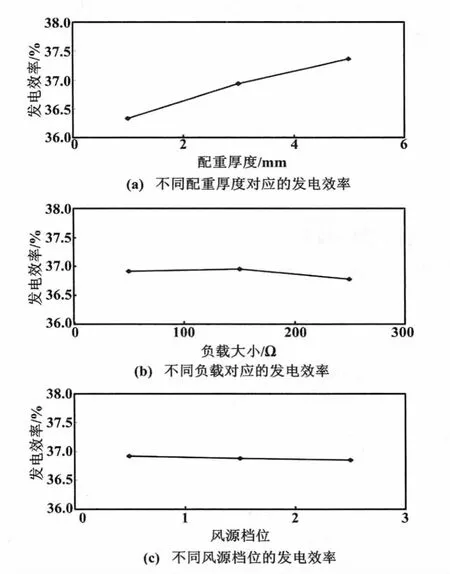
图4 正交试验数据极差分析图Fig.4 Range analysis of orthogonal experimental data

2.2 试验结果分析

随着配重厚度的增加，风机发电效率显著提高;而负载的变化也会使风机发电效率有一定变化;对于风速，随着风速的增大，发电效率有所提高，但影响并不显著。

3 转动惯量对效率的影响

完成正交试验后，补充单因素多水平试验，即在不改变风力、负载的情况下，只改变配重进行单项试验，进一步验证增加转动惯量对提高风机发电转换效率的影响。试验结果如表2所示。

表2 单因素多水平试验数据表Tab.2 Single factor and multi-level experimental data

由单项试验结果表明:风机的发电效率从不加配重时的36.12%增加到加上7 mm配重时的37.72%，效率有明显的提高，试验数据示意图如图5所示。

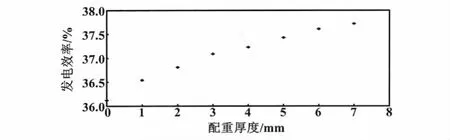
图5 单因素多水平试验数据图Fig.5 Single factor and multi-level experimental data chart

4 结束语

试验表明，小型风机在风洞试验室等较为理想的试验条件下，其最大效率为40% ～41%。通过单因素多水平试验，可以计算得出:在本试验环境中，从不加配重时的风机发电效率为36.12%提高到加2 mm厚的钢板时效率为36.81%，从加4 mm厚的钢板时效率为37.23%提高到加7 mm厚的钢板时效率为37.72%。

［1］李宇红，张庆麟.风力机风轮三维流动特性与气动性能的数值分析［J］.太阳能学报，2008，29(9):1172 －1174.

［2］赵振宙，郑源.螺旋型S型垂直风轮结构优化设计［J］.中国电机工程学报，2009(26):75－78.

［3］毛军，杨立国，郗艳红.大型轴流风力机叶片的气动弹性数值分析研究［J］.机械工程学报，2009，45(11):133 －139.

［4］祝贺，徐建源.风力机风轮气动性能三位流场数值模拟［J］.中国电机工程学报，2010(17):85－90.

［5］张仲柱，王会社，赵晓路，等.水平轴风力机风轮气动性能研究［J］.工程热物理学报，2007，28(5):781 －783.

［6］ 廖明夫，Gasch R，Twele J.风力发电技术［M］.西安:西北工业大学出版社，2009:105－107.

［7］ 赵欣.垂直轴三叶片风力发电机:中国，201010137349［P］.2010－08－04.

［8］伍艳，谢华，王同光.风力机风轮的非定常气动特性计算方法的改进［J］.工程力学，2008，25(10):54 －59.

［9］王福军.计算流体动力学分析-CFD软件原理与应用［M］.北京:清华大学出版社，2004:24－57.

［10］Altan B D，Atlgan M，Ozdamar A.An experimental study on improvement of a Savonius rotor performance with curtaining［J］.Experimental Thermal and Fluid Science，2008(32):1673 －1678.

［11］Liu T R，Ren Y S.Aeroelastic stability of wind turbine rotor based on Beddoes-Leishman model［C］∥IEEE International Symposium on Knowledge Acquisition and Modeling Workshop Proceedings，Wuhan，2008:605 －608.

［12］Kamojia M A，Kedarea S B，Prabhub S V.Performance tests on helical Savonius rotors［J］.Renewable Energy，2009(34):521 －529.

［13］Kunio I，Jitendro N R.Characteristics of wind power on Savionius rotor using a guide-box tunnel［J］.Experimental Thermal and Fluid Science，2007(32):580 －586.

［14］Menet J L.A double-step Savonius rotor for local production of electricity:a design study［J］.Renewable Energy，2004(29):1843 －1862.

［15］Veers P S，Ashwill T D，Sutherland H J，et al.Trends in the design，manufacture and evaluation of wind turbine rotor［J］.Wind Energy，2003，6(3):245 －259.

［16］Duquette M M，Visser K D.Numerical implications of solidity and blade number on rotor performance of horizontal-axis wind turbines［J］.Solar Energy Engineering，2003，125(4):425 －432.

［17］Chanin T，Sarun B，Sankar L N.Numerical simulation of the aerodynamics of horizontal axis wind turbines under yawed flow conditions［J］.Journal of Solar Energy Engineering，2005，127(4):464 －474.

［18］Abba A，Cercignani C，Valdettaro L.Analysis of subgrid scale models［J］.Computers and Mathematics With Applications，2003，46(4):521 －535.

［19］Wissink J G.DNS of separating low Reynolds number flow in a turbine cascade with incoming wakes［J］.International Journal of Heat and Fluid Flow，2003，24(4):626－635.