基于符号时间序列方法的多尺度股指波动分析

徐 梅，奚丹丹

(天津大学管理与经济学部，天津 300072)

股票市场的波动性意味着市场中存在不确定性和风险，全面、正确认识股市波动，对于市场投资者和监管者都有着重要的意义。鉴于金融市场的非线性特性，分形、混沌分析、符号时间序列分析(symbolic time series analysis，STSA)等非线性方法也被引入波动的分析中。

STSA方法广泛地应用在自然科学和工程领域，而在经济金融领域的应用刚刚起步［1-6］。文献［7］提出了基于符号时间序列分析的资产收益分析方法，能识别收益变化的主要模式，并实现对收益水平的预测，该方法也可用于波动序列的分析与预测。但该方法是从序列的整体性出发，没有考虑不同投资者的不同需求，如有些投资者可能关注短期的波动变化，而有些则对长期的波动变化更感兴趣。小波分析通过伸缩和平移能进行多分辨分析，区分不同时间尺度的不同变化，为各类投资者提供更精确的参考。

笔者将小波多分辨分析与STSA方法相结合，利用离散小波变换及其逆变换，将波动时间序列在多个尺度上分解，提取不同尺度的细节。对不同细节分量，采用STSA方法，确定其主要模式和异常模式，比较与原序列模式的异同。用该方法对上证综指与深证成指两个指数的波动序列进行实证分析，以验证该方法的可行性和有效性。

1 小波多分辨分析

在实际应用分析中，时间序列通常是离散型数据，因此通常采用离散小波变换，大多数采用的小波函数为:

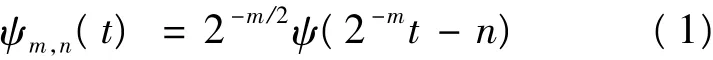
式中:m为尺度函数;n为平移系数;ψm，n(t)为小波函数。

根据文献［8］，L2(R)为平方可积函数集合，对于任意x(t)∈L2(R)可表示为:

式中，Wm，n= ∫x(t)ψm，n(t)dt为小波系数。对应m0级分解，用矩阵可表示为:

式中:W= [W1，W2，…，Wm0，Vm0]T;w=[w1，w2，…，wm0，vm0]T;Wm为第m级小波系数向量;wm为对应m级小波变换系数矩阵，为Nm×N维矩阵;Vm0为m0级以上小波系数总和;vm0为Nm0×N维矩阵。

则有:

式(3)和式(4)定义了 X的多分辨分析(multi-resolution analysis，MRA)，Dm为 X 在对应尺度τm的变化，称为m级细节分量;Sj(j=1，2，…，m0)为对应尺度 λj的j级平滑，表示 τj+1及以上尺度的细节与平滑之和。

2 符号时间序列分析

原序列经过小波多分辨分析，得到各级细节，展示了波动序列不同尺度上对应的变化，对各级细节进行符号化分析，可以更准确地把握不同尺度的变化规律。

数据符号化将数据用仅有的几个符号表示，从而降低噪声对统计算法的影响。对于给定时间序列{xt}，符号集大小为 n，引入划分 P={P1，P2，…，Pn-1}，将数据集划分为n个区间，采用统一划分方法，使每一个区间包含元素数量基本相等，每个区间用一个符号Sr(r=1，2，…，n)表示，如用符号集{0，1，2，…，n-1 }标记，将{xt}转化为符号序列{st}。

符号序列生成后，每个连续提取长度为L的子序列表示序列中某种确定的变化模式。如在分析波动序列时，取子序列长度L=4，符号集大小n=3，符号0、1、2表示低、中、高3种波动水平，则变化模式2012表示在4个连续的时间点上，依次为高波动、低波动、中波动、高波动。定义变化模式的支持数为对应子序列在时间序列中的频数。那么，对于完全随机序列，每个变化模式的支持数是相等的，反之，支持数的明显偏移反映序列在一定程度上的确定性。符号时间序列分析以支持数作为统计量，支持数较大的变化模式是序列的主要变化模式。同时，需要注意的是，时间序列的异常在某种程度上对后续的走势影响更大，因此时间序列的异常也是笔者研究的内容之一。按照异常的表现形式不同，时间序列的异常包括序列异常、点异常及模式异常，其中模式异常是在一条时间序列上与其他模式存在显著差异、具有异常行为的模式［9］。笔者研究的异常是时间序列的模式异常，异常模式在时间序列中出现概率较小，也就是支持数较低的变化模式。换句话说，支持数较低的变化模式，可以确定为时间序列的异常模式。针对原序列与各不同细节分量进行主要模式与异常模式的比较与分析，反映了不同尺度上的变化规律。

3 “已实现”波动的多尺度符号分析

选取上海证券交易所综合指数(简称上证综指)和深圳证券交易所成分指数(简称深证成指)的每5分钟收盘价作为样本序列，由这两个序列分别代表中国两个股票市场的价格。上证综指序列记为{P1t}，时间段为1991/07/26—2010/12/31，共132484个样本数据;深证成指序列记为{P2t}，时间段为 1991/07/26—2010/12/31，共132592个样本数据。首先由样本数据计算股指的“已实现”波动序列，再采用小波多分辨分析得到“已实现”波动序列的各级细节，将各级细节符号化，分析不同尺度上的主要模式与异常模式。

3.1 “已实现”波动

“已实现”波动(realized volatility，RV)是ANDERSEN等在金融高频时间序列的基础上提出的一种波动率度量方法［10］。通常RV为金融资产日内收益平方之和［11］，可表示为:

其中:rt，j为金融资产的日内收益;M为在[t，t+1]时间段内等间隔的采样次数。由此，得到上证综指、深证成指的“已实现”波动序列分别记为{RV1t}、{RV2t}，长度分别为2760和2768。

3.2 “已实现”波动序列的小波多分辨分析

根据式(4)对{RV1t}、{RV2t}进行小波多分辨分析，取 j=4 ，第 m(m=1，2，…，4) 级细节Dm对应的时间尺度为τm=2m-1，因此，D1～D4所对应的尺度分别为1、2、4、8个交易日。1、2个交易日对应于短期投资者，4、8个交易日由于时间跨度为一周和两周，对应中长期投资者。采用haar小波，得到每一级的细节分量。

图1为上证综指{RV1t}小波(4层)多分辨分析图。其中:s为原序列;a4为第4级平滑，反映了原序列的趋势概貌;di(i=1，2，…，4)为第i级细节，反映了对应尺度下RV的变化。同样，对深证成指{RV2t}进行多分辨分析，也可得到各级细节。

3.3 “已实现”波动细节分量的符号分析

给定序列{xt}，采用统一划分法，选取符号集大小n=3，用x1/3、x2/3分别表示1/3分位数和2/3分位数，作为划分3个区间的阈值，转化为符号序列{st}，即:

图1 上证综指RV1t小波(4层)多分辨分析图

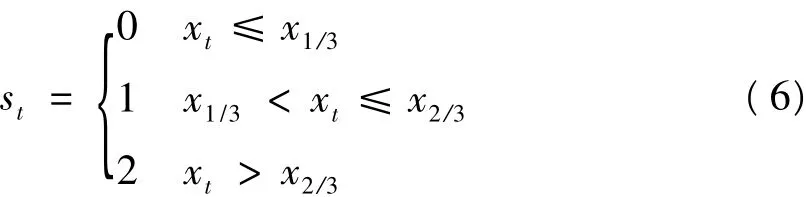
对于{RV1t}、{RV2t}以及各自的4级细节分量分别按式(6)转化为符号序列。符号0、1、2分别表示RV处于低、中、高3个不同的波动水平。

根据文献［7］选择字长的方法确定子序列长度L，令L从1开始增加，计算改进Shannon熵值，计算结果如表1所示。

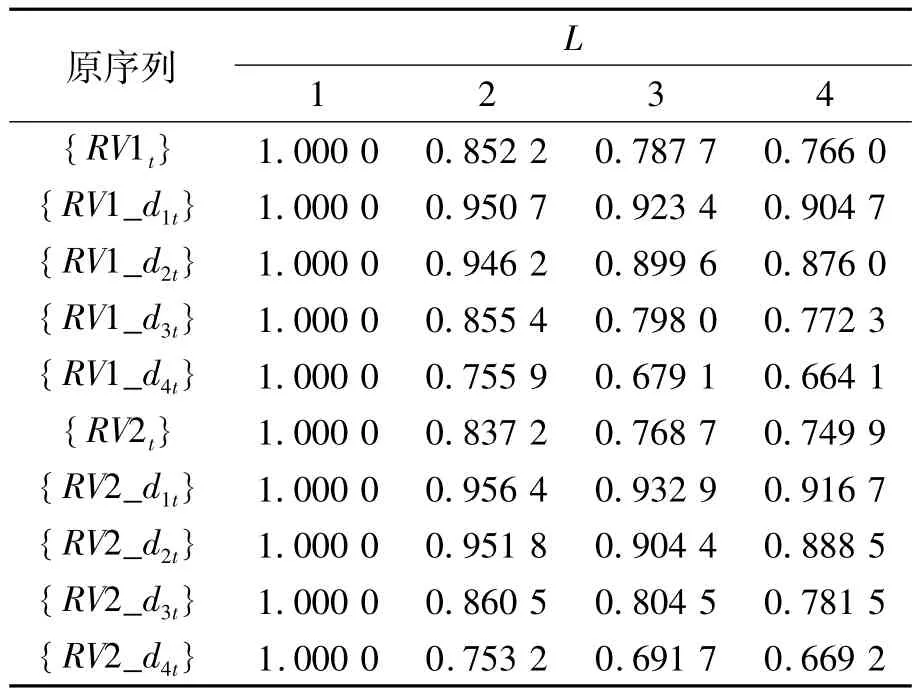
表1 符号序列的改进Shannon熵值

基于与文献［7］同样地考虑统计结果的可靠性，虽然熵值没有达到最小值，对每个细节符号序列都取L=4。由表1结果可知，在相同尺度上，对比上证综指与深证成指各个细节分量熵值，发现对于所有的L取值，深证成指细节分量d1、d2、d3的熵值都略大于上证综指对应分量的熵值，这说明以1、2、4天为尺度，深市RV序列中各种变化模式出现的概率更接近，随机性更强;沪市RV序列中主要变化模式更明显，确定性强于深市。对比原序列，{RV1t}的熵值却大于{RV2t}，表明作为一个整体，沪市RV序列的确定性更大，深市RV序列的随机性更强，说明进行多尺度分析是有必要的。

3.4 主要模式与异常模式分析

改进Shannon熵从总体上反映了序列中各种变化模式出现的情况。选取子序列长度L=4，统计得出各个子序列的不同的频数。频数越大，则子序列对应的变化模式的支持数越大，表明该变化模式是序列的主要模式;相反，支持数越小，则变化模式是序列的异常模式。

{RV1t}、{RV2t}及其各级细节的主要模式、异常模式、对应的支持数列于表2中。由表2的统计结果可以看到，各级细节分量的主要模式与异常模式皆不同于原RV序列。1～4级细节分量对应的尺度分别是1、2、4、8天。根据各个细节分量得出不同的结果，短期投资者应关注1、2天为尺度的主要模式和异常模式，中长期投资者应更侧重于4、8天为尺度的分析结果。在1、2、4天的尺度上，主要模式1111都占据了重要的地位，说明大多数连续4天都是中等波动水平。在8天的尺度上，0000模式与2222模式比1111模式更占优势，更倾向于与原序列的主要模式一致。由此，尺度越大，主要模式的分析结果与原序列越接近。异常模式虽然发生的可能性较小，但是影响却有可能是极大的。原序列的异常模式较多，尺度越小，异常模式越少，随着尺度的增加，异常模式越来越多，特别是未出现的异常模式。这是因为尺度增加之后，忽略的细节增加，使得上证综指和深证成指的RV都有了更多的未出现模式，这些未出现的变化模式几乎都包括了低、中、高3种波动水平，变化模式较复杂，因此在忽略更多细节的情况下，市场并没有表现出相关的波动变化。出现次数极少的异常模式通常与一些影响市场波动的重要事件相关，表3列出了小尺度下异常模式出现的时间及其对应的事件。在大尺度下，由于有些事件的影响是长期的，因此异常模式出现的时间与事件较难准确对应。

表2 RV与各级细节序列的主要模式与异常模式

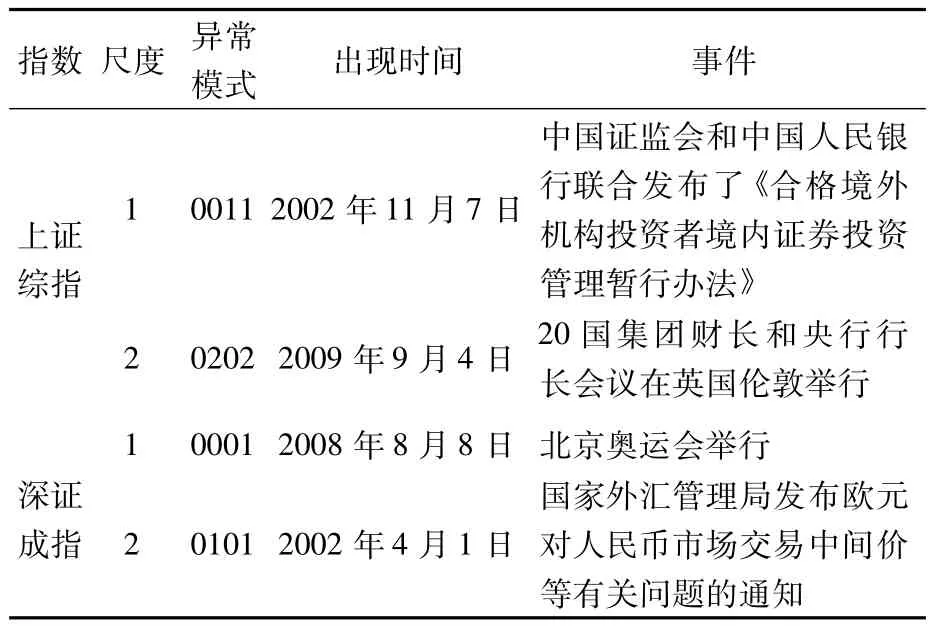
表3 异常模式与对应事件

4 结论

笔者首先根据小波的多分辨分析，将RV序列分解为不同尺度的细节分量，对原序列及不同的细节分量采用STSA方法，根据改进Shannon熵的计算结果选择子序列长度L，由子序列的支持数辨别不同尺度上的主要模式和异常模式。该方法简明直观，从不同尺度反映波动变化的规律，为不同投资者的投资决策和风险管理提供了参考。

对中国股票市场的上证综指、深证成指RV序列进行了实证分析，采用haar小波4层分解，选取符号集n=3和子序列长度L=4，确定了各指数RV序列的不同尺度上的主要模式与异常模式。实证分析验证了该方法的可行性和有效性，并得出了相关结论:不同细节分量对应不同的尺度，短期投资者应关注小尺度细节分量的分析结果，中长期投资者应关注大尺度细节分量的分析结果，因此，多尺度分析可为不同类型的投资者提供参考;尺度越大，主要模式越明显，异常模式越多，特别是未出现的异常模式，且分析结果越倾向于与原序列一致;出现次数极少的异常模式通常与一些影响市场波动的重要事件相关，尺度越小，异常模式与事件的对应越明确;笔者是以“已实现”波动序列作为研究对象，该方法同样也可以应用于其他金融时间序列的分析。

［1］SCHITTENKOPF C，TINO P，DORFFNER G.The benefit of information reduction for trading strategies［J］.Applied Financial Economics，2002(34):917-930.

［2］TAKUYA Y，KODAI S，TAISEI K，et al.Symbolic analysis of indicator time series by quantitative sequence alignment［J］.Computational Statistics and Data Analysis，2008(53):486-495.

［3］WISTON A R.The informational efficiency and the financial crashes［J］.Research in International Business and Finance，2008(22):396-408.

［4］JUAN G B，DAVID M G，WISTON A R.Symbolic hierarchical analysis in currency markets:an application to contagion in currency crises［J］.Expert Systems with Applications，2009，36(4):7721-7728.

［5］JUAN G B，WISTON A R.Multidimensional minimal spanning tree:the Dow Johns case［J］.Physica A，2008(387):5205-5210.

［6］BRIDA J G，PUNZO L F.Symbolic time series analysis and dynamic regimes［J］.Structural Change and Economic Dynamics，2003(14):159-183.

［7］徐梅，黄超.基于符号时间序列方法的金融收益分析与预测［J］.中国管理科学，2011，19(5):1-9.

［8］PERCIVAL D B，WALDEN A T.时间序列分析的小波方法［M］.程正兴，译.北京:机械工业出版社，2006:150-155.

［9］杜洪波.时间序列相似性查询及异常检测算法的研究［D］.沈阳:沈阳工业大学图书馆，2008.

［10］ANDERSEN T G，BOLLERSLEV T，DIEBOLD F X，et al.Exchange rate returns standardized by realized volatility are(nearly)Gaussian［J］.Multinational Finance Journal，2000(4):159-179.

［11］郭名媛，张世英.基于“已实现”波动的协同持续研究以及应用［J］.系统工程理论与实践，2006(5):30-31.