射流管式伺服阀反馈弹簧组件分析

赵开宇 袁朝辉 张 颖

西北工业大学，西安，710072

0 引言

电液伺服阀应用于许多现代控制系统中。由于工作油液的污染是引起伺服阀工作不正常的主要因素，因此希望有抗污染能力强的伺服阀，而由射流管前置级驱动的伺服阀由于射流喷嘴小，由杂质微粒等工作液中的杂物引起的危害小，保养管理容易，从构造上可以说是抗污染能力比较强的伺服阀。

由射流前置级驱动的伺服阀具有很广阔的应用前景，国内外都对它的特性进行了深入的研究。国外从20世纪60年代开始，射流管伺服阀广泛应用于航空航天以及民用工业部门，很多公司都有其射流管阀产品。

因为应用比较广泛，目前国内大部分厂家生产的伺服阀都是喷嘴挡板式电液伺服阀，射流管式伺服阀虽然具有抗污染性强等优点，但是因为它的设计制造相对困难，以及国外对射流管技术的限制［1］，故其在国内一直发展缓慢。本文在建立射流管式伺服阀的三维模型基础上，利用CATIA的有限元分析模块对阀的反馈弹簧组件进行分析，研究得出反馈杆最优的弯曲角度，进而在这个弯曲角度下分析了不同电磁力矩和反馈力对阀芯位移以及射流管偏角的影响关系。

1 射流管阀整体结构和原理

如图1所示，射流管式电液伺服阀的组成可以分为动铁式永磁力矩马达、射流管放大器、滑阀组件、反馈组件四大部分，各组件通过力反馈建立协调关系。

图1 射流管式电液伺服阀正视图

当给力矩马达输入控制电流时，衔铁会产生一个偏角θ，使得射流管从中立位置发生偏转，喷嘴发生位移xd，则喷嘴下面的两个接收孔接收的流体流量不同，喷嘴两接收腔便会形成Δp（Δp＝p1－p2）的压力差，阀芯在压力差Δp的作用下，带动反馈杆的端点由静止向一端移动xv，反馈杆继续变形，直到反馈杆作用于阀芯的力和油液作用于阀芯两端的压力达到动力学平衡，此时，反馈杆产生的力矩加上弹簧管产生的力矩，与电磁铁在电流i作用下产生的力矩，以及安全丝、进油管和板簧产生的力矩达到平衡，阀芯处于平衡状态。

射流管阀具有以下工作特点：改善了流量接收效率（90%以上的先导级流量被利用）、能耗降低；射流管先导级具有的无阻尼自然频率很高，因此它的动态响应较高；射流管先导级压力效率很高（输入满标定信号时，压力效率高达80%以上）；先导级的间隙较大，达到了200μm以上，那么先导级过滤器的寿命将会很长；大大改善了阀的频率响应，提高了功率级滑阀的增益，而且提高了阀的静动态性能，整个控制系统的性能也相应提高。先导级流量利用率可以达到先导级总流量的90%，几乎是双喷嘴挡板阀的两倍［2］。

2 反馈弹簧组件刚度计算

反馈杆和弹簧管的刚度通过衔铁组件力矩平衡关系来确定，其中衔铁组件的力矩平衡方程表示为［3］

这里，ic为控制电流，θ为衔铁偏转角度，那么式（1）左端为力矩马达产生的电磁力矩，其中：Kt为力矩马达中位电磁力矩系数；Km为力矩马达电磁弹簧刚度；S为拉氏算子。式（1）右端为作用在衔铁上的反馈力矩，其中：Ja为惯性系数；Ba为阻尼系数；Ka为弹簧管弹性系数；第四项和第五项为液流力矩；最后一项为反馈杆变形产生的力矩；r为转动中心到喷嘴中心的距离；Ap为喷嘴孔截面积；pp为接收孔压力差；Cp为喷嘴间隙出流的流量系数；ps为供油压力；xd为喷嘴位移；b为喷嘴到反馈杆端部的距离。反馈杆的刚度Kf＝F／ymax，F为作用于反馈杆端点的外力，ymax为反馈杆端点的位移。设y为长度x处截面上的位移，依据材料力学［4］有

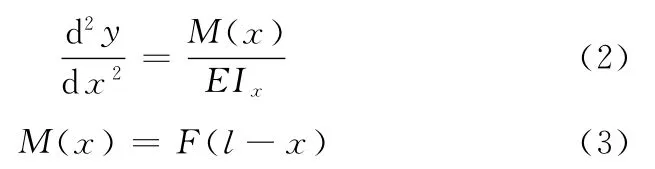
式中，E为材料的弹性系数；Ix为弹簧管截面惯性矩；l为弹簧管有效长度。

反馈杆的锥度K为

式中，D、d分别为弹簧管的外径和内径。

截面的惯性矩为

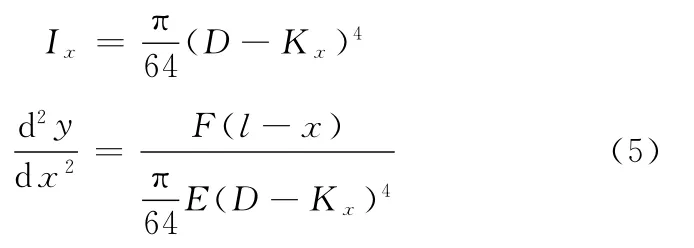
式中，kx为弹簧管和射流管间的间隙距离。

这里假设

则式（5）可表示为

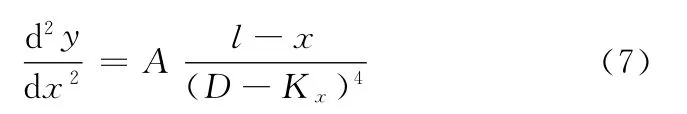
通过第一次积分可得

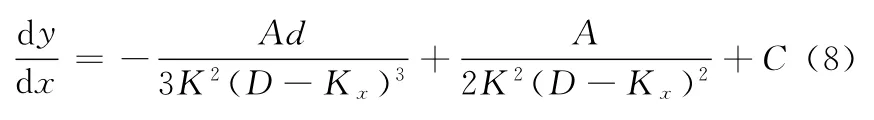
故有

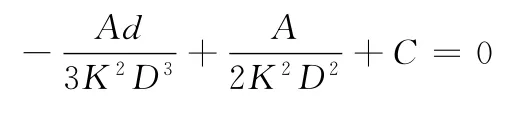
可得

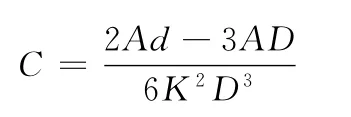
然后通过第二次积分可得

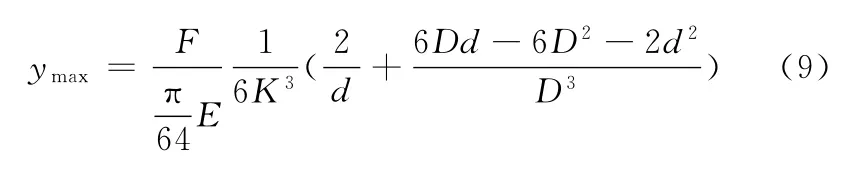
所以

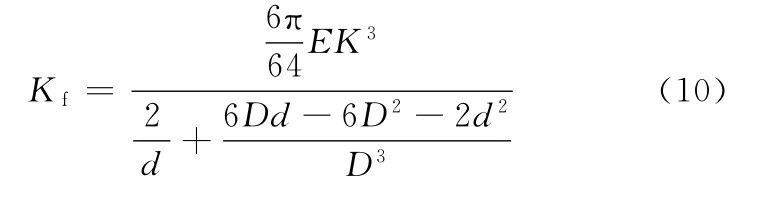
如果把喷嘴阀的反馈杆视作悬臂梁，则挠度为

式中，P为各个集中载荷标准值之和；J为转动惯量。

转角为

由于射流管反馈杆插入阀芯内不能转动，因此，转角θA＝0，变形可以简化为一个静不定问题，通过求支点反力矩MA＝Pl／2，解挠度fA的积分方程（其中积分常数可以由边界条件决定），可得可见射流管前置级阀的挠度仅仅为喷嘴挡板阀的1／4。而弹簧管可以看成一个空心的悬臂梁，管端的变形fA＝，转角（M 为电磁力矩）。而射流管伺服阀在结构上不同于双喷嘴挡板阀，它有一对支撑板簧，衔铁运动只有角度转动没有位移，这也是一个静不定结构，转角挠度f＝0，A因此，射流阀的转角θ是挡板阀的1／4，在射流管最大挠度点处，最大挠度为

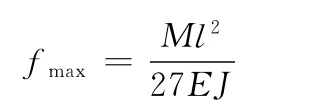
为了在射流管喷嘴处获得足够大的位移，射流阀的弹簧管比喷嘴挡板阀的弹簧管长，那么，射流管和反馈组件的变形力矩Mb为

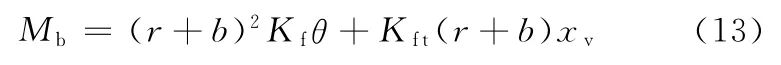
式中，Kf为反馈杆的刚度。

3 反馈杆改变参数的有限元分析

在反馈杆材料已经确定的情况下，影响反馈组件性能的因素有反馈杆弯曲角度、反馈弹簧片厚度等，其他各零件形状尺寸一般都相同，只要改变反馈杆弯曲角度，就可以改变反馈杆的性能指标。射流管伺服阀的理论分析计算的准确性不够好，主要依靠大量的试验来确定结构参数，且它的加工焊接工艺难度大，装配调试技术要求高，故设计射流管电液伺服阀时，力矩马达采用整体焊接结构，反馈杆顶端紧固在阀芯中间，以保证射流管伺服阀在严酷条件下工作可靠。反馈组件实际试验难度较大，这里采用有限元仿真分析的办法对射流管伺服阀的反馈组件进行分析［5］。

如图2所示，反馈组件模型主要由反馈杆、反馈杆上部的弹片、弹簧管和调零丝组成，进油管也会随着电磁力矩的扭转产生变形，计算中都要考虑在内。具体工作过程中，先是力矩马达产生的电磁力矩作用于衔铁上，对衔铁产生一个旋转扭矩，带动射流管和弹簧管有一个同向的偏转趋势，与此同时，反馈杆、调零丝、进油管和弹簧管都会产生一个与此相反的力矩来阻碍偏转，那么进入接收器的流量就会变化，这样通过整个动态过程的平衡来达到控制目的［6］。整个过程中反馈杆的反馈力对阀芯力平衡的影响很大，有必要深入研究。

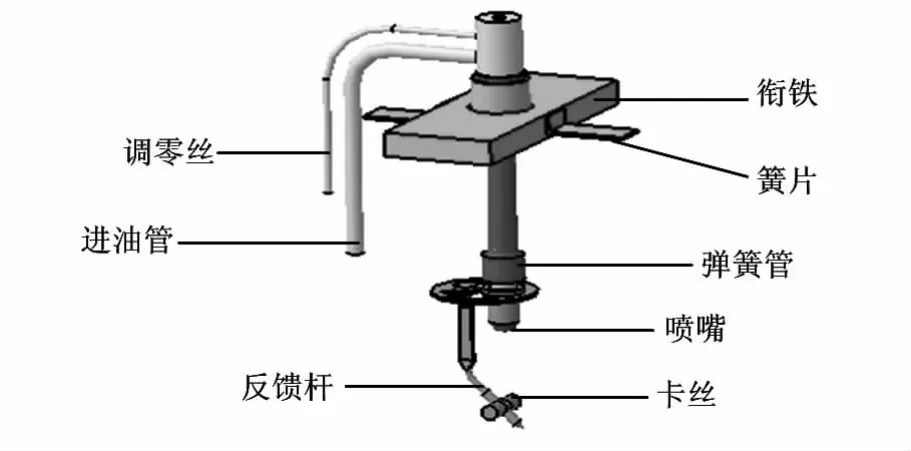
图2 射流管反馈杆组件模型

用CATIA软件进行有限元分析的步骤为［7］：①建立零件模型并导入分析模块。②完成前处理。先将反馈弹簧组件（包括反馈杆）材料定义为铍青铜，初步分析可以保持CATIA自动划分的网格参数；将反馈杆上部也就是射流管的下端和簧片两端以及调零丝和进油管的下端面固定；定义各个部件之间的接触关系时，衔铁和卡套之间是固定接触，卡丝和反馈杆之间是可滑动接触；定义载荷时在衔铁上部施加电磁力矩，在反馈杆中部的卡丝端面上施加力，也就是模拟了反馈力［8］；③进行求解计算，计算完成后进行可视化的数据分析，即后处理，可以看到在电磁力矩和反馈力的作用下，反馈杆变形明显，可以通过各个点的位置坐标确定各部分的位移。④根据应力分布和结果数据确定结构上的危险部位，判断零件设计是否满足工程应用要求，发现问题后需要调整结构设计方案，然后再次分析，如此循环直到满足需求［9］。当然，计算过程中还需要注意有限元分析方法的正确性和分析结果的有效性，下面利用CATIA的有限元分析功能对衔铁反馈组件进行分析。

在衔铁组件上面施加旋转力矩，射流管偏转一定角度，接收器两端接收的流量差别引起阀芯两端产生压差，推动阀芯向相反方向运动，带动反馈杆向一边运动，反馈杆变形产生抑制阀芯运动的反作用力。在施加于衔铁上的力矩不变的情况下，利用有限元分析模块Generative Structural Analysis对反馈杆在不同弯曲角度下的反馈应力进行分析。

由图3可以看出随着反馈杆弯曲角度的变化（固定反馈杆末端的各个自由度位移），反馈杆上的应力将发生变化。具体变化关系如表1所示。

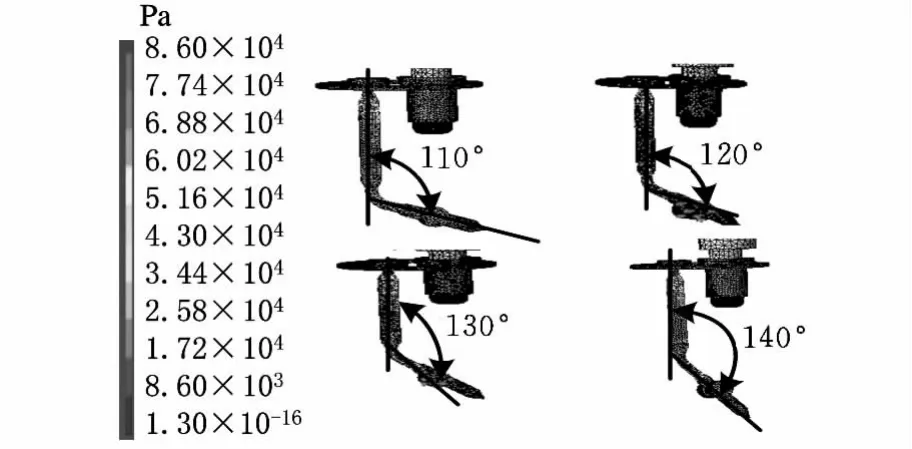
图3 不同弯曲角度下射流管反馈杆组件应力云图

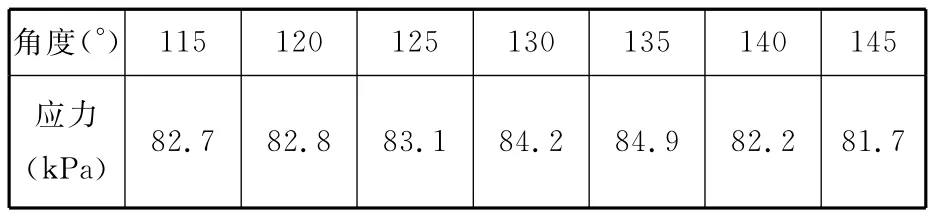
表1 弯曲角度和反馈应力的关系

利用MATLAB分析以上数据，插值拟合出它们的数据关系曲线，如图4所示。由图4可以看出，随着反馈杆弯曲角度的变化，应力并不是一直增大，则反馈力Ff与弯曲角度α之间关系可以表示为

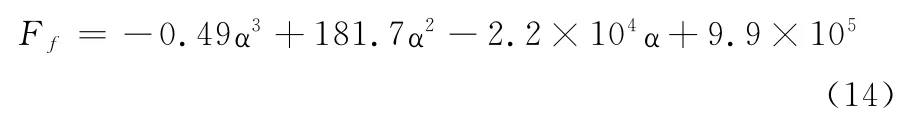
由图4可知，弯曲角度为135°时反馈杆的反馈效率较高，后面的分析将反馈杆弯曲角度取为135°。

图4 反馈杆不同弯曲角度的应力曲线

4 电磁力矩和阀芯位移以及射流管偏转角度的关系

利用上述有限元模型，固定反馈杆弯曲角度为135°。 通过有限元划分将反馈组件划分为33 116个节点、128 004个元素。改变作用于衔铁上的旋转力矩和作用于反馈杆上的作用力，模拟阀芯以及射流管喷嘴运动位移。有限元计算出的位移如图5所示。

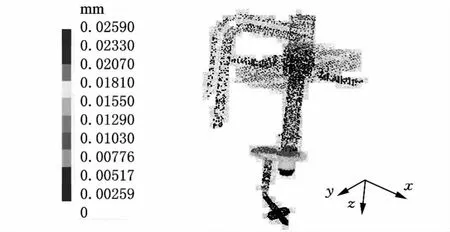
图5 力矩和反馈力作用下的阀芯位移

从图5可以看出阀芯位移受电磁力矩和反馈杆反馈力的影响。通过改变参数可以计算得到表2所示几组数据的关系。

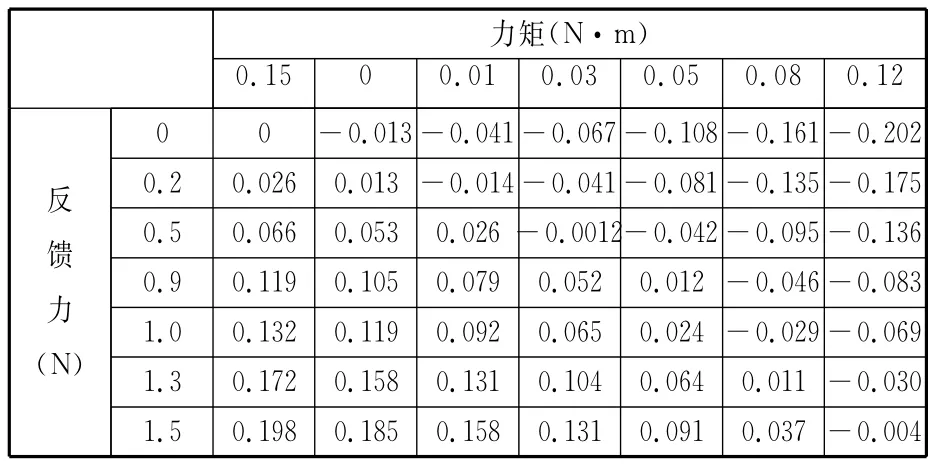
表2 力矩和反馈力对阀芯位移影响 mm

以上仿真试验的数据中，力矩逆时针取正，位移方向向右取正。利用MATLAB拟合它们的关系，如图6所示。

考虑反馈杆作用于阀芯上的力和电磁力矩对阀芯位移的影响，拟合得到阀芯位移与电磁力矩和反馈力的函数关系：

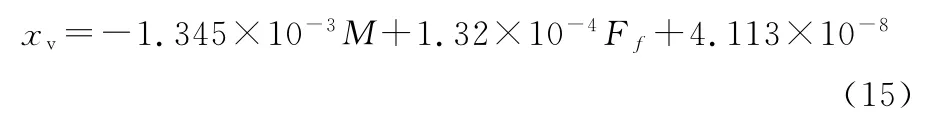
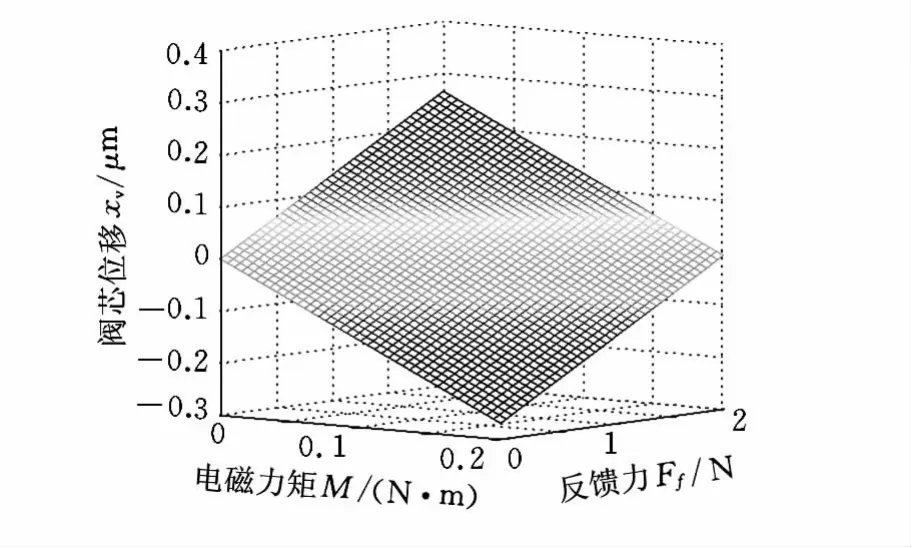
图6 力矩和反馈力与阀芯位移之间的关系

同时，在CATIA有限元计算过程中还可以得出射流口位移与电磁力矩以及反馈力之间的关系，如图7所示。

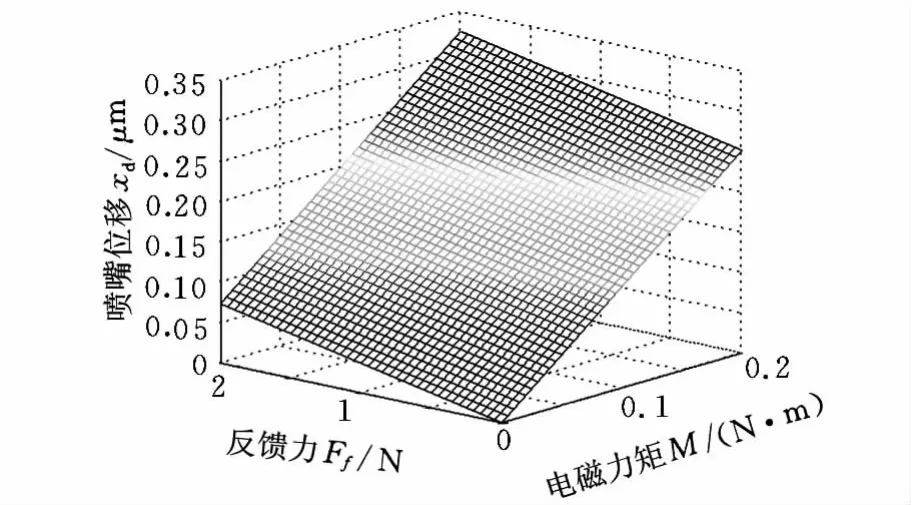
图7 力矩和反馈力与喷嘴位移之间的关系

利用MATLAB工具可以拟合出射流口位移与电磁力矩和反馈力的函数关系：

又因为xd／ls＝θ（ls为射流管长度），故运用式（15）和式（16）可以推导得出电磁力矩M 和反馈力Ff关于射流管偏转角度和阀芯位移的函数：

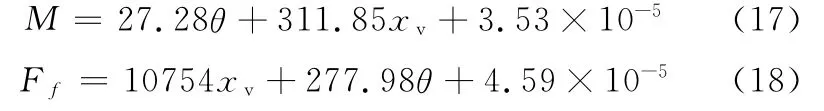
至此就得到了基于有限元计算方法的射流管电液伺服阀反馈弹簧组件的静态特性关系，这些关系的得出为阀的整体动态仿真奠定了基础。

5 结论

（1）通过有限元仿真的方法，模拟了反馈杆不同弯曲角度情况下反馈力的变化规律，进而确定了反馈杆弯曲角度在135°左右时，整体反馈效率较高。

（2）取反馈杆弯曲角度为135°，分析电磁力矩、阀芯位移以及反馈力之间的关系，获得了它们相互影响的关系式。

（3）取最优的反馈杆曲角度，利用有限元计算得出了电磁力矩、反馈力和弯曲射流管偏转角度之间的关系，对整体阀的动态性能分析具有基础作用。

（4）在集中参数数学推理不精确的情况下，在射流管伺服阀实际仿真试验中利用有限元分析的方法可以得到更为精确的结果，在射流管伺服阀的设计过程中应该充分利用先进的仿真工具，得到满意结果。

［1］上海船舶设备研究所.射流管电液伺服阀专题讲座［J］.液压与气动，2010，1（4）：91－92.Shanghai Marine Equipment Research Institute.An Introduction of Jet Pipe SV Valve［J］.Chinese Hydraulics ＆ Pneumatics，2010，1（4）：91－92.

［2］李培滋，王占林.飞机液压传动与伺服控制［M］.北京：国防工业出版社，1979.

［3］王占林.液压伺服控制［M］.北京：北京航空学院出版社，1987.

［4］李如萍.射流管式水压电液伺服阀研制及特性研究［D］.武汉：华中科技大学，2011.

［5］Coakley J L，Calif C.Method and Apparatus for Improved Jet Pipe Valve：USA，46244［P］.1972－07－16.

［6］訚耀保，孟伟.非对称喷嘴挡板式电液伺服阀特性分析［J］.中国机械工程，2011，22（8）：956－961.Yin Yaobao，Meng Wei.Characteristics of Electrohydraulic Servovalve with an Asymmetric Nozzle Flapper［J］.China Mechanical Engineering，2011，22（8）：956－961.

［7］Zoller G C，Ohio C.Variable Gain Jet Pipe Servo Valve：USA：801292［P］.1971－06－23.

［8］李胜，阮健，孟斌.2D数字伺服阀频率特性研究［J］.中国机械工程，2011，22（2）：215－221.Lisheng，Ruanjian，Mengbin.Study on Frequency Response for a 2DDigital Servo Valve［J］.China Mechanical Engineering，2011，22（2）：215－221.

［9］Maskrey R H，Thayer W J.A Brief History of Electrohydraulic Servo Mechanisms［J］.ASME Journal of Dynamic Systems Measurement and Control，1978，141（3）：4－7.