基于FLAC采场底板应力-应变本构关系研究
2013-09-07许海涛李永军康庆涛
许海涛,李永军,康庆涛
(1.河北省矿井灾害防治重点实验室,河北 三河065201;2.华北科技学院安全工程学院,河北三河065201;3.中国矿业大学 (北京)煤炭资源与安全开采国家重点实验室,北京100083)
华北地区煤田水文地质条件十分复杂,裂隙以斜交和垂直地层等形式赋存于各类地层中,分布面积大,裂隙及溶蚀裂隙发育,含水性强,矿井涌水量大、突水频率高,煤矿安全生产形势严峻。对郑州、晋城、徐州、永城及两淮地区50多个矿井的调研及井下观测,裂隙是矿井突水主要的导水通道,且多数淹井、淹工作面的重大突水事件与底板裂隙发育有关。煤层底板突水是煤层下伏承压水冲破底板隔水层的阻隔,以突水、缓发或滞发的形式进入工作面,造成矿井涌水量增加或淹井的自然灾害,为矿井生产的五大灾害之一[1-2]。几十年来,国内外许多学者对矿井突水机理进行了一些有益的探索,取得了大量的研究成果。“突水系数”[3]、“强渗通道”[4]、“水岩应力”[5]、“零位破坏与原位张裂”、“关键层”及“下三带”等理论学说,都从各个方面揭示了突水发生的机理和预测方法,对于矿井安全生产起到了积极的指导作用[6-7]。
随着我国一些重点矿区的奥陶纪灰岩岩溶水突出问题日益受到重视,对煤层底板承压水的突水机理已展开了广泛的研究,矿山压力是影响底板承压水突出的重要因素,是底板破坏的力源;了解煤层底板的应力分布是研究煤层底板破坏深度的重要前提,有利于加深对突水机理的认识。本文拟采用FLAC模拟软件求解采空区的围岩应力-应变关系,分析不同阶段采空区底板应力变化过程,并建立应力、应变随采场深度变化的本构关系,以解释其对底板突水的影响。
1 采空区底板垂直应力变化过程
工作面开挖以后的瞬间,在采场周边的初始地应力被释放,应力由三向状态变为两向或单向应力状态,使采场周边附近的围岩的应力重新分布,即底板受力随着距采场距离而逐渐加大到到原岩应力状态。由于围岩应力的重新分布引起底板出现变形,在一定条件下,底板的变形发展导致围岩破坏、失稳。
开挖前,底板岩层处于原岩应力状态,如图1(A)、图2所示,且视作均布载荷,简化底板受力模型。开挖后瞬间底板岩层受力如图1(B)、图3所示。工作面开挖以后的瞬间,采空区底板岩层上部支承力被去掉,但深部底板岩层的弹塑性恢复应力与原岩应力垂直分量相等且均匀分布,底板有向虚线位置发生位移的趋势。由于采空区底板岩层下部支承力被去掉,而且底板有向虚线位置发生位移的趋势,致使底板应力平衡被打破,导致在采场周边的初始地应力被释放,围岩受力随着距采空区底板距离加大而逐渐加大,然后逐渐减小到原岩应力状态。随着围岩应力调整,围岩的应力重新分布成为图1(CD)、图4所示应力状态。
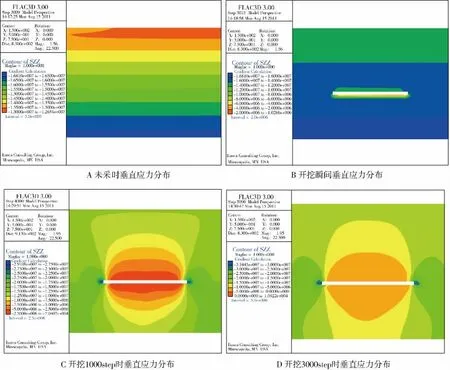
图1 采场垂直应力变化图
2 采场底板应力-深度本构关系研究
通过数值模拟计算结果可得底板不同深度测点的垂直应力变化曲线如图5所示,底板垂直应力与底板深度关系曲线如图6所示。当采场应力重新分布基本平衡时,底板处的垂直应力为0MPa,随着深度的增加,垂直应力逐步增加,根据以上数据统计,运用SPSS数学软件进行回归分析,可得到式(1)。
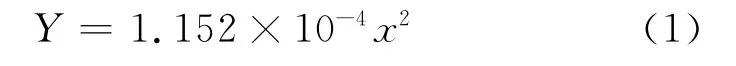
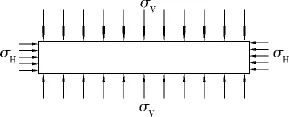
图2 未开挖时底板受力分析图
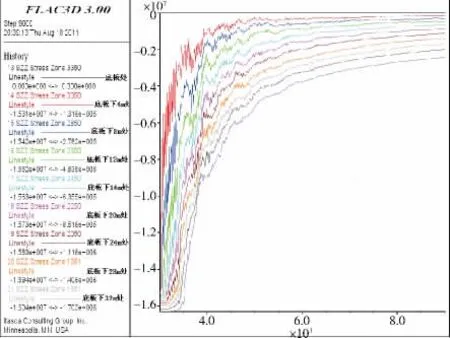
图5 底板不同位置处垂直应力变化曲线
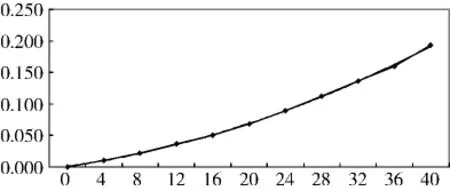
图6 底板垂直应力与底板深度关系曲线
式中,Y为垂直应力与原岩应力的比值;X为采场底板深度,m。
此时垂直应力
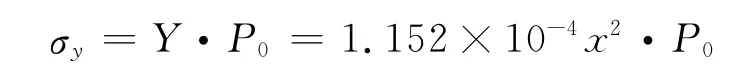
式中P0为原岩应力,MPa。
当y=1时,x的值代表工作面回采对底板的影响极限深度;当y>1时,底板垂直应力可由原岩应力P0求得。由公式(1)可知:当采空区下方隔水层深度一定时、厚度一定时,隔水层由于采动而引起的力学变化,如当隔水层为底板下方20~50m,则y20=0.06,y50=0.38,即隔水层上部垂直应力为:p1=y20×p0,下部垂直应力p2=y50×p0。
3 采空区底板应变规律分析
采空区底板垂直位移图见图7。通过数值模拟计算结果可得,底板不同深度测点的垂直位移变化曲线如图8所示,底板深度与位移关系曲线如图9所示。当采场应力重新分布基本平衡时,底板处的垂直变形最大为104.6mm,随着深度的增加,垂直位移逐步减小;根据以上数据统计进行回归分析,其数学表达式见式(2)。
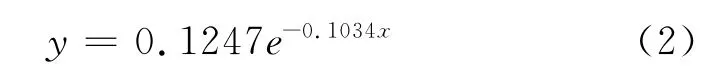
此时垂直方向的应变
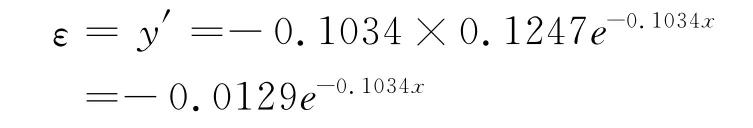

图7 采空区底板垂直位移图
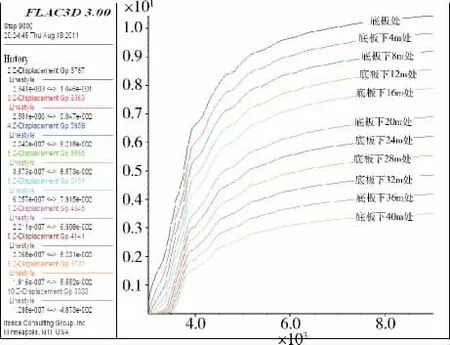
图8 底板下方不同深度垂直位移变化曲线
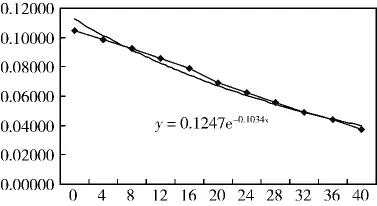
图9 底板深度与位移关系曲线图
式中:y为底板深度为x时的垂直位移,m;x为采场底板深度,m;ε为底板深度为x时的应变;[ε]为底板岩体的屈服应变。
当ε>[ε]时,底板将产生屈服破坏;当ε<[ε]时,底板未破坏。
式(2)为本文中数值模拟结果的统计分析,尚未考虑其他因素的影响。
4 结论
通过以上分析可知以下内容。
1)工作面开挖以后的瞬间,在采场周边的初始地应力被释放,应力由三向状态变为两向或单向应力状态,使采场周边附近的围岩的应力重新分布,在一定条件下,底板的变形发展导致围岩破坏、失稳。
2)建立了深度与应力的本构关系,当采场应力重新分布基本平衡时,底板处的垂直应力接近于0MPa,随着深度的增加,垂直应力逐步增加。
3)建立了底板深度与应变的本构关系,当采场应力重新分布基本平衡时,底板处的垂向变形最大,随着深度的增加,垂向位移逐步减小。
4)本公式只是对本计算模型数据的回归分析,尚未考虑时间因素,尚需进一步深入研究。
[1]杨天鸿,唐春安,刘红元,等.承压水底板突水失稳过程的数值模型初探[J].地质力学学报,2003,9(3):281-288.
[2]魏久传,李白英.承压水上采煤安全性评价[J].煤田地质与勘探,2000,28(4):57-59.
[3]沈光寒,李白英,吴戈.矿井特殊开采的理论与实践[M].第1版.北京:煤炭工业出版社,1992:285-290.
[4]许学汉,王杰.煤矿突水预报研究[M].第1版.北京:地质出版社,1991:228-235.
[5]吴基文,樊成.煤层底板岩体阻水能力原位测试研究[J].岩土工程学报,2003,25(1):67-70.
[6]王作宇,刘鸿泉.承压水上采煤[M].北京:煤矿工业出版社,1992:102-113.
[7]荆自刚.峰峰二矿开采活动与底板突水关系研究[J].煤炭学报,1984,9(2):20-23.
