含瓦斯煤固气耦合动力学模型及其应用研究

刘 军 ，孙东玲，孙海涛，林府进

(1.中煤科工集团重庆研究院瓦斯分院，重庆 400037；2.瓦斯灾害监控与应急技术国家重点实验室，重庆 400037)

煤的渗透性是煤层气开发过程中关键因素，孔隙压力、有效应力以及基质收缩/膨胀对煤的渗透性具有重要影响[1]。 “动态渗透率”这一关键性因数，已得地面煤层气开发的广泛认可[1-2]。煤层气开发中广泛应用的P-M、Seidle-Huitt模型和Shi-Durucan模型，其共同点是假设煤岩体处于单轴应变状态以及竖向应力恒定的基础上,该假设的合理性有待商榷，特别研究采动影响下煤层开发，以上模型还有待改进[4-7]。周军平、汪志明等[8-9]建立了包括孔隙压力、有效应力以及基质收缩耦合作用动力学模型,但是并没有考虑到瓦斯流动中吸附扩散作用。随着研究的深入，建立综合考虑考虑孔隙压力、有效应力以及基质收缩耦合作用的固气耦合模型对煤层气勘探、开发和开采工艺确定、产能预测及预防瓦斯突出等将起到重要作用[10]。因此，本文在广大学者研究的基础上,综合考虑各因素，建立含瓦斯煤固气耦合动力学模型，并将其应用到生产实践。

1 含瓦斯煤固气耦合动力学数学模型

1.1 动力学模型的基本假设

模型引入如下假设：①含瓦斯煤是一种均质弹性体；②煤层被单相瓦斯饱和且温度恒定；③煤层瓦斯在孔隙-裂隙多重介质中渗流符合Darcy定律，扩散符合Fick扩散定律，并不考虑煤层基质块与裂隙质量交换；④吸附/解吸以及煤岩裂隙瓦斯压力变化会使煤颗粒体积应变发生改变，且产生应变在三个方向上相等。

1.2 动力学模型应力场方程

应力场变化服从应力方程、平衡方程、本构方程。

1)应力方程

由太沙基有效应力原理，有效应力方程为

由式(1)、式(2)得到总应力方程

2)平衡方程

3)本构方程

根据假设，煤体在弹性变形阶段遵守广义的胡克定律，即

式中，λ为拉梅常数；εv为体积应变；G为剪切模量；δij为Kronecker符号。

多孔介质煤体的变形包含本体变形和结构变形[11]。结构变形主要是外应力引发煤粒之间位置相对错动产生的整体变形，是永久性塑性变形。本体变形主要包括热膨胀变形、吸附瓦斯膨胀变形和煤体骨架受瓦斯压力的压缩变形。在忽略温度变化前提下，煤体的本体变形只有：吸附瓦斯膨胀变形和煤体骨架受瓦斯压力的压缩变形。即认为含瓦斯煤层受到地应力和作用在煤体单元孔裂隙结构中的瓦斯压力以及瓦斯吸附膨胀产生的膨胀应力而发生变形。吴世跃[12]针对吸附瓦斯膨胀变形进行深入研究，从理论上推导了煤体膨胀应力和膨胀应变的计算公式。

式中：σsw为吸附膨胀应力，Pa;εsw为吸附膨胀应变，％；a为极限吸附量，m3/kg；b为吸附常数，MPa-1；R为瓦斯摩尔常数，8.3143J/(kg·K)；T为煤体温度，K；υ为泊松比；Vm为摩尔体积，22.4×10-3m3/mol；P为孔隙压力，MPa；ρc为含瓦斯煤体视密度，kg/m3。

在工程实践中[13-16]得出，因孔隙流体压力变化而引起的固体颗粒体积变化而引起的变形由式(8)表示。

式中：εp为瓦斯压力引起的应变；Δp为瓦斯压变化，MPa。

将于煤体的本体变形表示为：εs=εsw-εp，所以有式(9)成立。

根据式(2)、式(9)求的σij的表达式

σij=

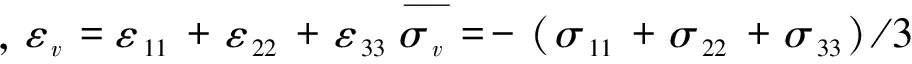
1.3 瓦斯流动方程

煤体是孔隙-裂隙的双重介质体，包含孔隙系统和裂隙系统，假定瓦斯在裂隙系统中以渗流形式运动，在孔隙系统扩散运动。而瓦斯流动数学模型包含了瓦斯流动连续性方程、瓦斯运动控制方程、煤层瓦斯状态方程和瓦斯含量方程四个基本方程组成，以下是分别对以上四种方程的描述。

1.3.1 连续性方程

瓦斯的在裂隙系统和孔隙系统中连续方程为式(13)、式(14)，在孔隙-裂隙二重介质中，裂隙中自由煤层气的渗流量比孔隙系统中吸附煤层气扩散要大得多，所以可以忽略孔隙系统通过扩散直接进入钻孔或煤壁的气体，而仅把孔隙系统的扩散解吸看作向裂隙系统补给的内质量源，此时煤层气的扩散渗流方程组就由煤粒吸附煤层气扩散方程与裂隙系统渗流方程，所以得到瓦斯流动连续质量方程(15)。

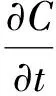
式中：C为单位体积煤层所含有吸附状态煤层气的质量浓度，kg/m3；ρg为瓦斯压力p时瓦斯气体密度，kg/m3；Jc为扩散流体通过单位面积的扩散速度,kg/(s·m2)。

1.3.2 流动的方程

1)煤层瓦斯渗流的状态方程。钻孔抽采下煤层瓦斯在煤体内的流动符合Darcy渗流规律[17]。

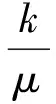
当气体在煤岩多孔介质中流动时,由于气体分子平均自由通道程与孔裂隙的直径处在同一量级上,气体分子就会与通道壁面相互作用,从而造成气体分子沿孔隙表面滑移,增加了分子流速,这一现象称为分子滑移现象[18]。这种由气体分子和固体分子间的相互作用产生的效应称Klinkenberg 效应(式(17))，因此考虑Klinkenberg效应的瓦斯渗流运动方程为(18)。

式中：V煤层瓦斯渗流速度矢量，m/s；k为渗透率，k0为初始渗透率，m2；m为klinkenberg系数。

2)扩散运动方程。气体在多孔介质中扩散满足Fick扩散定律[19]，写为

J=-D

式中：J扩散流体通过单位面积的扩散速度,kg/(s·m2)；D扩散系数,m2/s；C扩散流体质量浓度,kg/m3。

1.3.3 状态方程

根据假设瓦斯被看作理想气体，瓦斯流动视为等温过程，则其状态方程

式中：β煤层瓦斯的压缩因子，kg/(m3·Pa)，且有：β=Mg/ZRT；Mg为瓦斯气体分子量，kg/(K·mol)；R为一般气体常数，kJ/(kmol·K)；T为气体的温度，K；Z为压缩系数。

1.3.4 含量方程[19]

式中：Cf、Ca分别为游离和吸附瓦斯含量，kg/m3；pn为大气压；ρn为参考大气压下瓦斯密度，kg/m3；φ为煤体孔隙度；A为煤中灰分；W为煤中水分；a为极限吸附量，kg/m3；b为煤的Langmuir压力参数，MPa-1;ρc为当前压力下瓦斯密度,kg/m3。

根据式(15)～(21)得出瓦斯流动控制方程

φ+

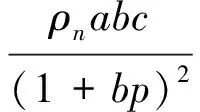
式(22)与式(12)构成了煤层气与煤层耦合动力力学模型，但二者之间需靠渗透率k和孔隙度φ建立耦合关系。

1.4 动态渗透性与孔隙度模型

Zhang等人[20-23]建立普遍应用的动态孔隙度与渗透率模型，近年来得到广泛的应用，鉴于文章篇幅不再推导。

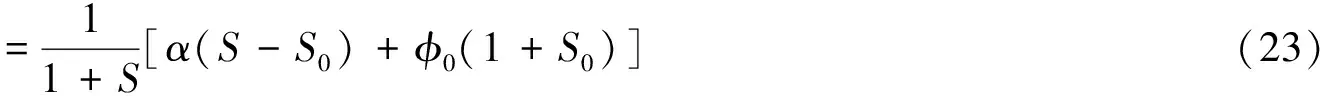
其中

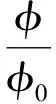
煤是典型的孔隙介质，若煤的体积模量K远小于煤基质的体积模量Ks,游离瓦斯和吸附产生的变形忽略不计，则上式可以得

式(26)与文献[13]得到的孔隙度关系式是完全相同的。

式中：εv为当前体积应变；εv0为初始体积应变；εs为现在因瓦斯压力变化产生变形和吸附变形之和。

式(23)求导得出孔隙率的变化率。

将式(12)、式(22)、式(23)、式(24)、式(27)整理就得到含瓦斯煤层与煤层气耦合动力学模型，即式(28)。

2 固气耦合动力学模型应用

固气耦合动力学模型具有广泛应用，在此利用该模型借助COMSOL Multiphysics软件对山西某矿3#煤层顺层钻孔抽采煤层瓦斯有效半径进行数值求解，验证模型的同时，也为现场工程起到指导作用。

2.1 几何物理模型

根据已有研究[24-26]，钻孔抽放数值分析采用二维平面模型。考虑到工作面的煤层赋存条件、地应力状态和瓦斯钻孔抽排设计条件，建立了其几何物理模型见图1。物性参数见表1。

2.2 模型的初始条件和边界条件

在所取研究域内，其初始条件和边界条件如下。

1)煤层瓦斯初始条件：t=0；p=P0。

式中：P0为煤层瓦斯压力初始值P0=0.69MPa。

2)分析域内边界条件为

3)应力场初始位移μ=0；ν=0。

4)应力边界条件为：煤层顶部边界上承受着上覆岩层的重量应力为F=6.5MPa ，同时考虑煤体自重，位移边界条件在分析域的下端边界y=0以及左端和右端边界上x=0和x=100为位移约束边界；r为抽采半径,p1为抽采负压。

图1 单一顺层钻孔抽排瓦斯数值模拟的几何模型

表1 某矿含瓦斯煤层物性参数

3 数值模拟的结果分析

鉴于该矿瓦斯压力低，用含量变化判定瓦斯抽采效果更佳，因此对瓦斯含量变化进行分析。图2为不同抽采时间含量的变化图，图2中可以看出，随着抽采时间的增加，瓦斯含量不断的减小，钻孔抽采的影响范围不断的增加，瓦斯流场范围在抽采负压作用下逐渐扩大，为进一步定量描述钻孔抽采下瓦斯含量的变化，取模型中以点(50，3.125)和点(100,3.125)组成的剖面线，和取点A(51，3.125)、B(52,3.125)、C(55,3.125)以及点D(50,4.125)和E(50,5.125)对上述瓦斯含量变化进行分析。图3为不同抽采时间剖面线上瓦斯含量的变化图，图4为点A、B、C、D、E处瓦斯含量随时间的变化。

根据图3、图4知，钻孔周围瓦斯含量下降较快，瓦斯含量梯度较大，但是随着时间的增加，瓦斯含量减小，瓦斯含量的降低梯度也减小，这说明钻孔在抽采的初始阶段，瓦斯的抽放量很大，经过一段时间之后，瓦斯抽采量将趋于稳定，以上分布图与文献[26-28]模拟结果一致。根据图4中B、E点和A、D点瓦斯含量对比分析知，在同一时间下，距离钻孔相同距离点的瓦斯含量比水平方向含量降低快，这是因为受到钻孔开挖致渗透率增加。

图2 不同抽采时间瓦斯含量的变化图

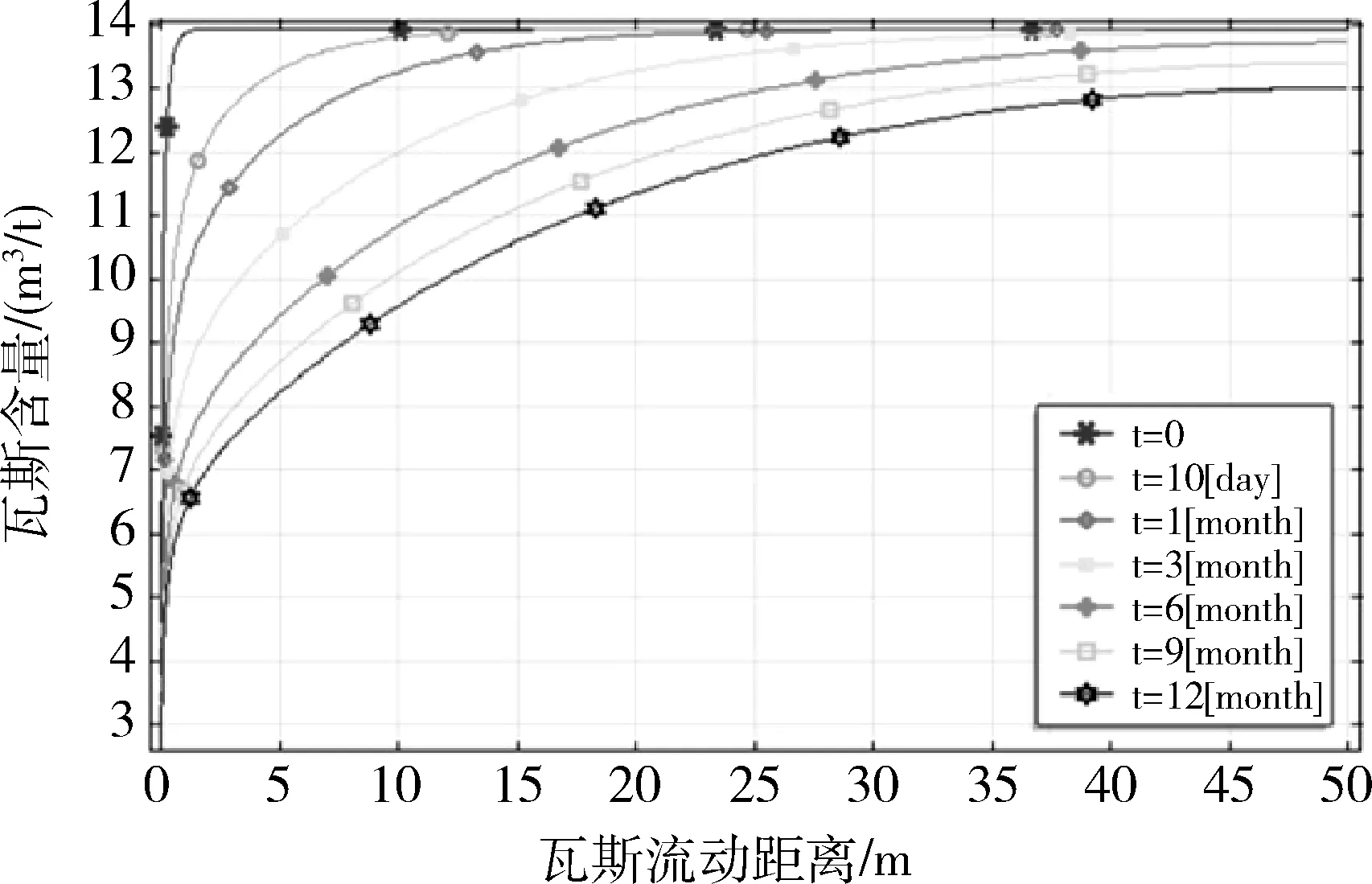
图3 不同抽采时间剖面线上瓦斯含量的变化图

图4 点瓦斯含量随时间的变化图

根据《煤矿瓦斯抽采基本指标》(AQ 1026-2006)中规定，在钻孔有效抽采半径内，需将煤层瓦斯含量降到8m3/t。因此，把瓦斯含量降到8m3/t为指标确定钻孔有效抽采半径。依靠这个指标根据图3该矿抽采一年的有效半径约为4.5m。这一数据与该矿在抽采工程中取得数据以及顺层钻孔合理布置参数实验得到的半径基本一致，证明了此数学模型的正确性。最终将钻孔的间距由原来的5m，提高到7～10m，在渗透率相对低区域钻孔间距小，渗透率高区域钻孔间距大。通过对抽采参数监测，最终保证综放面安全生产预抽率(25％～30％)，取得了良好的抽采效果。

4 结论

从瓦斯流动理论出发，以体积应变为桥梁通过煤层的孔隙度、渗透率方程将煤层应力场方程与瓦斯流动场方程耦合，建立含瓦斯煤固气耦合动态数学模型。借助多物理场数值模拟软件，分析本层单一顺层钻孔的瓦斯含量变化，得出特定条件下瓦斯抽采有效半径,并通过与现场实验与实际抽采数据分析验证瓦斯抽采有效半径正确性。固气耦合动力学模型的建立将对煤层气开发和防治煤与瓦斯突出具有理论和工程指导意义。

[1]李培超,孔祥言,曾清红，等.煤层渗透率影响因素综述与分析[J].天然气工业,2002,22(5):45-49.

[2]邓泽,康永尚,刘洪林，等.开发过程中煤储层渗透率动态变化特征[J].煤炭学报,2009,34(7):947-951.

[3]郭衍茹,练章华，魏臣兴.气井的流固耦合渗流场分析[J].断块油气田,2012,19(4):481-484.

[4]Seidle J P,Jean sonne M W,Erickson D J.Application of matchstick geometry to stress dependent permeability in coals[ C].SPE 1992,243-261.

[5]PalmerI,MansooriJ.How pemeability depends on stress and pore pressure in coal beds :a new model[J].Soc.Pet.Eng.Res.Eng,1998,12 :539- 544.

[6]赵阳升,胡耀青,杨栋，等.三维应力下吸附作用对煤岩体气体渗流规律影响的实验研究[J].岩石力学与工程学报,1999,18(6):651-653.

[7]孙培德.变形过程中煤样渗透率变化规律的实验研究[J].岩石力学与工程学报,2001,20(S1):1801-1804.

[8]周军平,鲜学福,姜永东，等.考虑有效应力和煤基质收缩效应的渗透率模型[J].西南石油大学学报,2009,31(1):4-8.

[9]张健,汪志明.煤层应力对裂隙渗透率的影响[J].中国石油大学学报,2008,32(6):92-95.

[10]狄军侦,殷志祥,刘建军.应力作用下煤层气非稳定耦合渗流模型及数值模拟[J].中国煤田地质,2007,19(4):36-38.

[11]李传亮,孔祥言,徐献芝，等.多孔介质的双重有效应力[J].自然杂志,1999,21(5):288-297.

[12]吴世跃,赵文,郭勇义.煤岩体吸附膨胀变形与吸附热力学的参数关系[J].东北大学学报：自然科学版,2005,26(7):683-686.

[13]李培超,孔祥言,卢德唐.饱和多孔介质流固耦合渗流的数学模型[J].水动力学研究与进展,2003,18(4):419-426.

[14]付玉,郭肖,贾英，等.煤基质收缩对裂隙渗透率影响的新数学模型[J].天然气工业,2005,25(2):1-3.

[15]冉启全,李士伦.流固耦合油藏数值模拟中物性参数动态模型研究[J].石油勘探与开发,1997,24(3):61-65.

[16]陶云奇,许江,程明俊.含瓦斯煤渗透率理论分析与试验研究[J].岩石力学与工程学报,2009,28(2):3363-3370.

[17]周世宁,林柏泉.煤层瓦斯赋存与流动理论[M].北京:煤炭工业出版社,1990.

[18]Jones F O,Owens W W.A laboratory study of low gas sands[J].J Pet Tech,1980:1631-1670.

[19]杨其銮,王佑安.煤屑瓦斯扩散理论及其应用[J].煤炭学报,1986(3):87-93.

[20]孙培德.SUN模型及其应用[M].杭州:浙江大学出版社,2002.

[21]Detournay E,Cheng AHD.Fundamentals of poroelasticity[M].In:Fairhurst C,editor.Comprehensive rock engineering,1993,2:113-71.

[22]J.G.Wang a,Akim Kabirb,Jishan Liu.Effects of non-Darcy ?ow on the performance of coal seam gas wells[J].International Journal of Coal Geology,2012(93):62-74.

[23]Hongbin Zhang Jishan Liu,D.Elsworth.How sorption-induced matrix deformation affects gas ?ow in coal seams:A new FE model[J].International Journal of Rock Mechanics & Mining Sciences,2008(45):1226-1236.

[24]Shi J Q,Durucan S.Changes in Permeability of Coalbeds During Primary Recovery Part 1:Model Formulation and Analysis[C].Paper 0341 proc.2003 International Coalbed Methane Symposium,University of Alabama,Tuscaloosa,Alabama(May).

[25]王宏图,江记记,王再清，等.本煤层单一顺层瓦斯抽采钻孔的渗流场数值模拟[J].重庆大学学报,2011,34(3):24-29.

[26]司鹄,郭涛,李晓红.钻孔抽放瓦斯流固耦合分析及数值模拟[J].重庆大学学报,2011,34(11):105-110.

[27]刘清泉,程远平,王海锋，等.顺层钻孔有效瓦斯抽采半径数值解算方法研究[J].煤矿开采,2012,17(2):4-8.