机器人运动功能位姿矩阵研究与应用

韩 雪

（1.辽宁工程职业学院，辽宁 沈阳 110136；2.铁岭技师学院，辽宁 铁岭 112006）

1 概述

工业机器人末端执行器的动作是通过各关节的运动传递来实现的，各个关节的运动直接决定了其末端执行器最终能实现的动作、功能，因此机器人运动功能位姿描述对于机器人运动功能设计有十分重要的意义。机器人的运动功能位姿描述一般是通过运动功能位姿矩阵来表述的，本文详细论述了机器人运动功能位姿矩阵的构成及应用。

2 运动功能位姿矩阵的构成

运动功能位姿矩阵用于表示机器人末端执行器在整个机器人中相对机座的位置和姿态变化。它由几何齐次坐标变换矩阵和运动齐次坐标变换矩阵构成。

2.1 几何齐次坐标变换矩阵

几何齐次坐标变换矩阵用于描述机器人从机座坐标系变换到末端执行器坐标系所经历的一系列坐标变换。其中，绕X轴旋转的旋转变换矩阵是：

绕Y轴旋转的旋转变换矩阵是：

绕Z轴旋转的旋转变换矩阵是：

沿X轴移动的移动变换矩阵是：

沿Y轴移动的移动变换矩阵是：

沿Z轴移动的移动变换矩阵是：

2.2 运动齐次坐标变换矩阵

运动齐次坐标变换矩阵用于描述几何齐次坐标变换后关节的姿态，如绕Z轴转动的回转关节矩阵是：

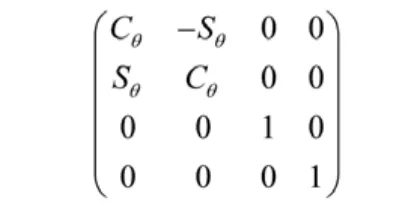
绕Z轴移动的移动关节矩阵是：

3 应用举例

如图所示机器人结构简图（见图1）。

3.1 图纸分析

该机器人共包括三个自由度，依次为关节1的回转运动，关节2 的回转运动，关节3 的直线运动。

3.2 几何齐次坐标变换分析

从机座坐标系X0-Z0 变换为关节1的坐标系X1-Z1需沿Z 轴移动c0距离，几何齐次坐标变换矩阵为：

从关节1坐标系X1-Z1变换为关节2的坐标系X2-Y2需绕X轴转动90°并沿Z轴移动c1，几何齐次坐标变换矩阵为：

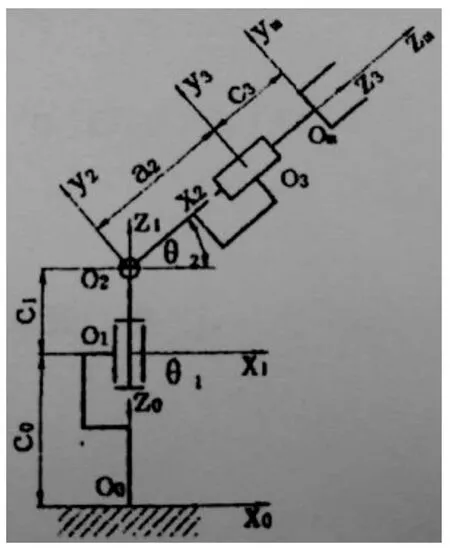
图1 机器人结构简图

从关节2坐标系X2-Y2变换为关节3的坐标系Y3-Z3需绕Y轴旋转90°并沿X轴移动2a距离，几何齐次坐标变换矩阵为：

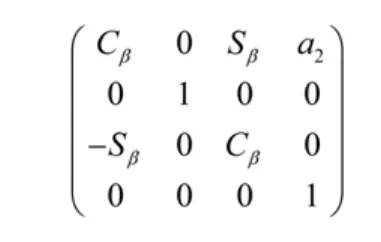
从关节3坐标系Y3-Z3变换为末端执行器坐标系Ym-Zm需沿Z轴移动3c距离，几何齐次坐标变换矩阵为：

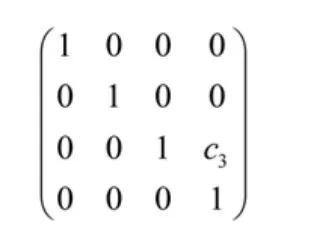
3.3 运动齐次坐标变换分析

关节1作绕Z轴旋转的回转运动，运动齐次坐标变换矩阵为：

关节2作绕Z轴旋转的回转运动，运动齐次坐标变换矩阵为：

关节3作沿Z轴移动的直线运动，运动齐次坐标变换矩阵为：

3.4 列出运动功能位姿矩阵

其中：

结语

通过观察运动功能位姿矩阵，可以清楚的了解机器人自由度个数，各关节运动性质及排列顺序，在基准状态时关节轴的方位等等。

[1]关慧贞，冯辛安.机械制造装备设计（第3版）[M].北京：机械工业出版社，2012.