GPU／CPU协同粗粒度并行计算及在城市区域震害模拟中的应用①

韩 博，熊 琛，陆新征，叶列平

（清华大学土木工程系 土木工程安全与耐久教育部重点实验室，北京 100084）

0 引言

近年来，全世界各地接连发生了严重的地震灾害。例如2008年的汶川地震，2010年的海地地震以及2011年的东日本地震。这些地震都造成了万人以上的人员死亡以及巨大的经济损失［1］。因此，科学预测城市区域建筑破坏，发现抗震薄弱环节，对减少地震损失、提高震后应急救援效率，具有重要的科学意义和实用价值。

本文提出基于精细化模型、非线性时程分析和GPU／CPU协同粗粒度并行计算的区域建筑震害预测方法，对并行计算的效率进行详细的讨论，并通过一个中等大小的城市案例展示该方法的优势。

1 区域建筑震害预测方法的发展

在过去的30年，基于易损性矩阵的区域建筑震害预测方法得到广泛应用［2］，它通过给出不同场地烈度下某类型建筑达到不同破坏状态的概率（此概率一般可通过历史震害经验调查得到）来对震害损失进行预测。由于易损性矩阵方法具有简单易行的优点，因而被广泛采用。

但是易损性矩阵方法只能给出宏观和统计意义上的预测结果，无法反映具体建筑物的详细损伤情况，也难以反映某一具体地震事件的特点。因此，基于能力－需求分析的建筑震害预测方法也得到大量研究，并集成在 HAZUS等震害预测软件中［3－5］。例如，HAZUS 99 的 Advanced Engineering Building Modules（AEBM）［4］通过计算建筑弹塑性能力谱和地震需求谱的交点得到性能点，进而根据性能点来判断建筑物的损失情况。该方法相对易损性矩阵方法有了很大的进步，它能够计算出每栋建筑的位移和最大绝对加速需求，因此可以更加准确的对结构构件和非结构构件进行损失预测，也可以考虑不同地震动之间的差异。然而，该方法仍存在以下两方面的问题：（1）将实际建筑物简化为单自由度体系，无法考虑高阶振型影响；（2）采用基于静力推覆的能力－需求分析，无法考虑地震动的一些特性（例如速度脉冲）的影响［6］。

为解决以上问题，出现了以下两方面的改进研究：（1）采用更加精细化的模型，以提供更多的结构动力特性信息［7］；（2）采用非线性的时程分析，以充分考虑地震动的各种特性［8］。但是，虽然基于精细化模型的非线性时程分析在单体建筑中已经得到了广泛的应用［9］，但是考虑到区域城市海量的建筑数量，该方法的推广一直存在很大的难度。随着计算能力的飞速发展，2008年Hori和Ichimura［10］基于精细化结构模型和非线性时程分析提出了Integrated Earthquake Simulation（IES）平台。该平台同时涵盖了地震动的生成、结构分析以及损失预测3个分析流程，并且可以采用多种精细化结构模型（如离散元模型和纤维梁模型）［11］，是未来城市区域震害预测的一个重要发展方向。但是对于震后应急响应等一些需要迅速获取计算结果的情况，IES需要强大的计算平台（如超级计算机）作为支持［12］，而这意味着高昂的运营费用和维护成本，因此限制了IES的广泛应用。

2 GPU粗粒度并行计算

最近几年，图形处理单元（GPU）技术飞速发展并在通用计算领域得到的广泛应用。虽然GPU单核的计算能力相对CPU较弱，但是GPU的处理核心数远多于CPU，因此相同价格的GPU相对CPU具有更高的计算性能［13］。随着NVIDIA公司发布了 CUDA （Compute Unified Device Architecture），GPU通用计算的编程难度被大大降低。目前GPU计算在生物、电磁场、地理等领域得到了大量的应用［14－16］。

最能发挥GPU性能的是细粒度的并行计算［17］，即将每个子任务划分成许多更细小的操作步，然后GPU在操作步层面对子任务进行并行计算。这种并行方式在神经网络以及有限元领域得到了很广泛的应用［18－19］。但是这种并行计算方式需要对GPU程序进行细致的调试以实现对大量的操作步高效的运算，程序实现难度较大。而相对于细粒度的并行，粗粒度的并行方式则更容易实现。粗粒度的并行计算方式采用的是基于相对独立的子任务的并行而不是操作步的并行。这种并行方式在优化和控制领域都有应用［20］。当满足以下情况时，粗粒度和细粒度的并行效率相当：

（1）子任务的数量远多于GPU计算的核心数；

（2）每个子任务的计算量比较适中，能够独立在一个GPU核心上完成；

（3）各个子任务之间不需要太多的数据交换。并且计算过程中不需要全局同步，每个GPU核心上的子任务可以按顺序逐个的进行计算。

幸运的是区域城市建筑震害预测分析可以满足以上三个特性。虽然整个城市有成千上万栋的建筑，但是如果通过采用适当的计算模型使每栋建筑结构的计算量不超过GPU单核的计算能力，则每栋单体建筑的计算就能被看作一个相对独立的计算子任务。此外不同建筑的地震响应相对独立，不同GPU线程之间几乎不需要进行数据交换。因此GPU数百计的计算核心可以实现几百栋建筑同时计算，这样计算效率将非常高。

3 程序构架

整个程序包括3个模块：前处理模块、结构分析模块和后处理模块［21］。前处理模块的主要任务是获取计算模型的主要参数，并且选择地震场景进行非线性时程分析。后处理模块主要展示模拟结果并预测损失。

计算分析模块是程序的核心，由CPU和GPU协同完成计算任务。其中CPU负责文件读写、任务分配等工作，GPU负责完成每一栋单体建筑的结构非线性时程计算。为了平衡计算量和计算精度之间的关系，本研究采用多自由度集中质量剪切模型来模拟每个单体建筑物（图1，2）［21］。建筑结构每层的质量被集中在了对应的节点上，并利用非线性滞回模型模拟建筑结构的层间滞回行为。集中质量剪切模型的计算精度主要取决于层间滞回模型的选取，目前已有很多相关研究［22－24］。本文主要借鉴了广泛使用的HAZUS损失分析软件中的层间滞回模型［25］。

为了避免隐式动力计算的收敛性问题，并提高GPU并行计算效率，本文采用中心差分法求解动力方程［26］。动力方程中的阻尼采用经典瑞利阻尼。

图1 单体建筑的集中质量剪切模型示意图Fig．1 Diagram of shear model of individual building＇s lumped mass．

4 性能对比分析

为了对比本研究提出的基于GPU／CPU协同粗粒度并行计算的结构分析模块的性能，开发了一个功能相同的基于CPU平台的计算程序，具体对比结果如下。

4．1 对比算例和计算平台

（1）随机生成不同结构类型的1 024栋建筑，如表1所示；

（2）采用广泛使用的El Centro地震动时程记录［27］进行对比分析。地震动时程记录的峰值加速按照200cm／s进行调幅；

（3）计算时长为40s，时间步为8 000步；

（4）为了避免读写速度的影响，下文中的计算时间不包括硬盘的读写时间。

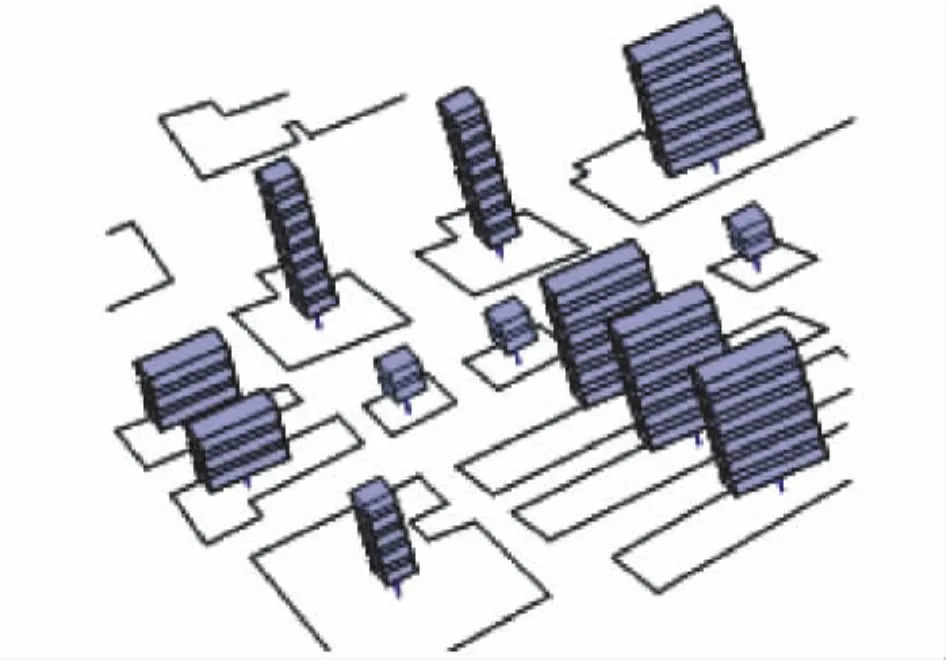
图2 群体建筑的集中质量剪切模型示意图Fig．2 Diagram of shear model of community building＇slumped mass．

表1 性能对比分析中使用的建筑结构类型分布情况Table 1 Distribution of building structure types used in the performance comparison and analysis

计算平台如表2所示。

以上两套计算平台均为2011年采购，在当时两者价格基本相同。因此采用以上两套平台可以用于比较相同价格情况下的性能差异。

4．2 对比分析结果

首先采用单栋建筑对比CPU平台和CPU／GPU协同计算平台的计算效率。楼层数和单栋建筑平均计算时间的关系如图3所示。从图中可以看出对于一栋建筑GPU／CPU协同计算的时间要长于CPU计算的时间，即单颗GPU核心的计算能力要明显弱于CPU的计算能力。此外还可以注意到对于一栋10层楼建筑，采用单精度计算GPU／CPU协同计算平台需要5s，如果采用双精度计算则需要8s。然而CPU平台的单精度和双精度计算时间非常接近（双精度还稍快），这是因为使用的CPU是基于64位构架，其默认计算精度就是双精度。

表2 对比采用的计算平台Table 2 Computing platform used in the comparison

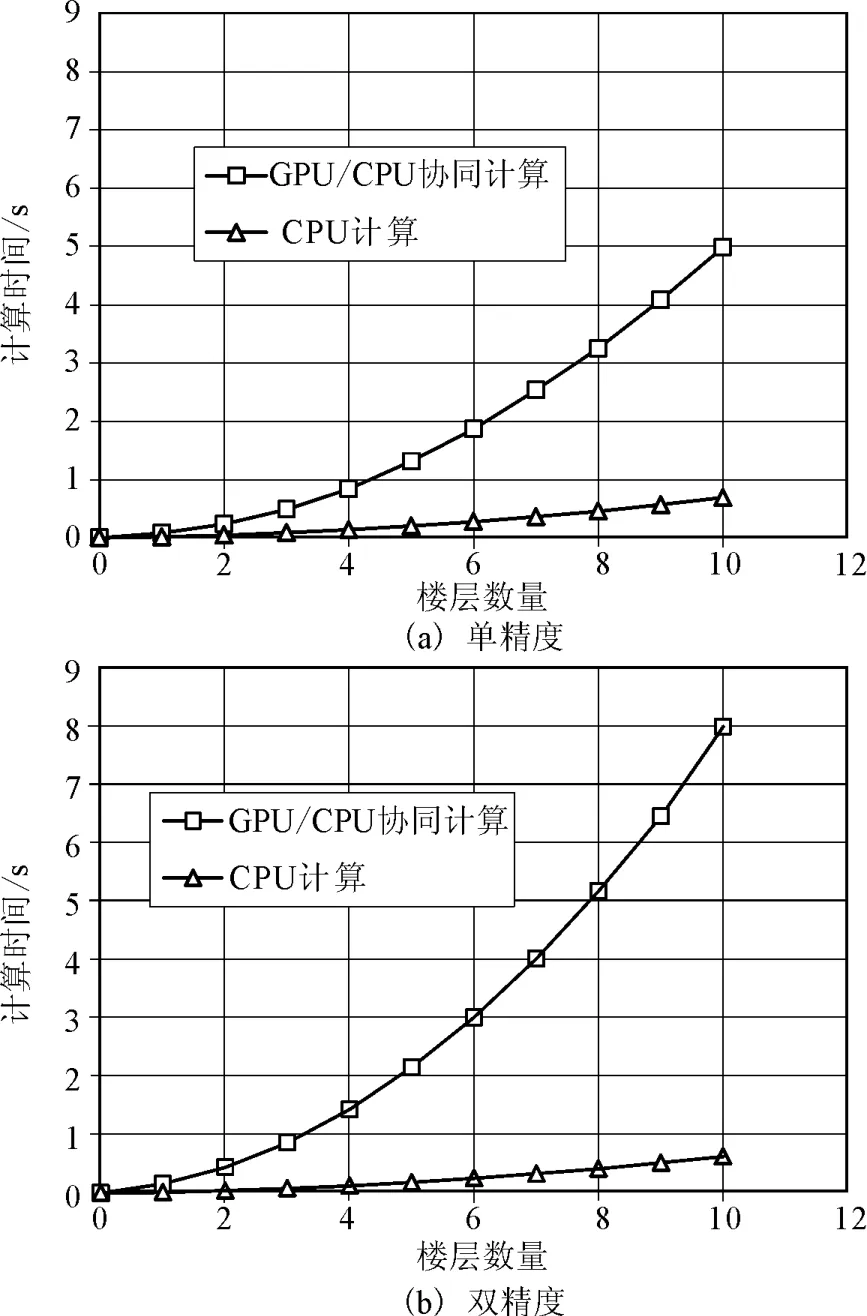
图3 单体建筑的层数和计算时间的关系Fig．3 Relationship between storeys of individual building and computation time．

对于1 024栋建筑物，如果改变CUDA的block size（每个计算块的线程数量），得到的计算时间如图4所示，可见当程序的block size为32时程序能达到最高的计算能力。这是因为当采用CUDA进行并行计算的时候每32个线程组成一个wrap，而GPU计算任务的最小单位是一个wrap［28］。因此，如果block size小于32时GPU的性能不能充分发挥。而当单精度的block size大于520或者双精度的block size大于260时，将超出GPU中速度最快的寄存器的容量（本平台GPU每个block只能使用32K的32位寄存器，可存储32 768个单精度数或16 384个双精度数），因此也会导致并行效率下降。

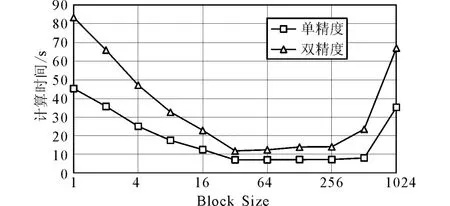
图4 在GPU／CPU平台上对1 024栋建筑进行分析的计算时间和block size之间的关系Fig．4 Relationship between block size and computation time used to analyze 1 024buildings on GPU／CPU platform．

在1 024栋建筑中，随机选取不同的建筑数量在CPU平台和GPU／CPU平台上进行性能对比（GPU／CPU平台的block size是32），结果如图5所示。CPU的计算时间与建筑的数量基本上是线性的关系。然而GPU／CPU协同计算平台的计算时间则主要取决于计算时间最长的那个线程（图5）。此外GPU／CPU协同计算平台双精度计算的曲线上有几个曲线的突跃，这是由于GTX460的双精度计算是在特殊函数单元中完成的 （Special Function Unit），其数量是CUDA核心数的1／6。这个问题可望在Fermi架构的Tesla GPU上得到修正，因为其双精度计算是直接在CUDA核心上完成的［28］。

由GPU／CPU平台与CPU平台的计算时间对比可以看出GPU对繁重的非线性时程计算具有巨大的速度优势。如图6所示，当对1 024栋建筑进行单精度计算时，采用GPU／CPU协同计算的时间仅是CPU计算的1／39，如果采用双精度则是1／21。此外，文献［28］对比了GPU单精度和双精度计算结果，发现差异不足0．1%，因此对于区域建筑震害模拟而言，单精度计算已经可以满足要求。

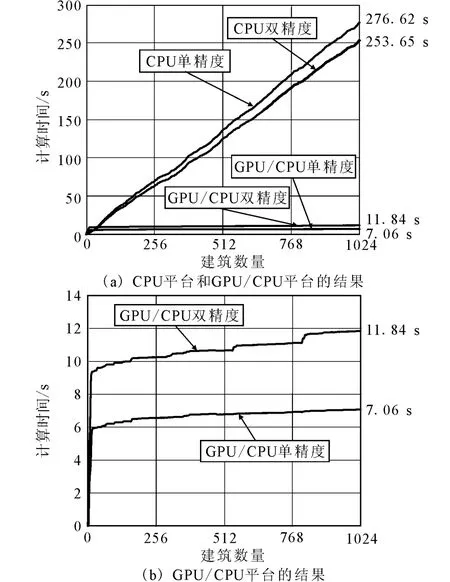
图5 CPU平台和GPU／CPU平台的计算效率对比Fig．5 Contrast of computational efficiencies of CPU platform and GPU／CPU platform．

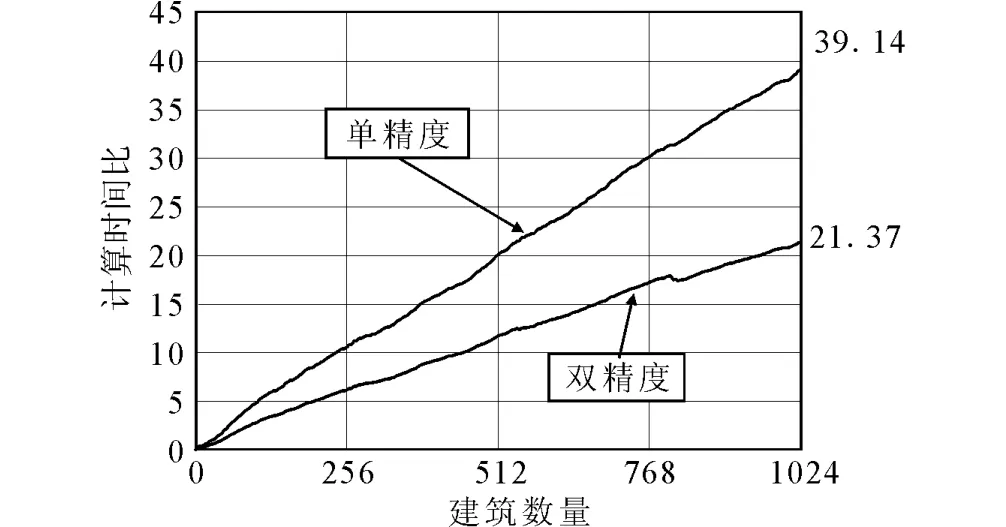
图6 CPU计算平台和GPU／CPU协同计算平台的计算时间比与建筑数量之间的关系Fig．6 Relationship between computation time ratio of CPU computing platform and GPU／CPU collaborative computing platform and the number of buildings．

5 算例分析

以某中等城市为例应用本文中提出的方法对该城市进行了建筑震害模拟，并讨论本文方法的优势。该中等城市总共有4 255栋建筑。将该地区的建筑按照表3对不同年代的建筑进行了抗震等级分类［29］。对不同的抗震设计等级将根据HAZUS中提出的方法确定建筑结构的层间滞回参数［25］。不同结构类型建筑的统计信息如表4所示。

分析采用了3类地震动数据：远场地震动，近场无速度脉冲地震动，近场有速度脉冲地震动。对于每一类地震动，从FEMA P695推荐的地震动数据库中分别选取5条（表5）［30］。根据该城市的设防烈度，对于小震、中震、大震分别采用70 200和400 cm／s2的地面峰值加速度对选取的地震动记录进行调幅。由于本文主要讨论建筑震害模拟方法，因此没有考虑场地对地震动的影响，每栋建筑都采用相同的地震动记录。

表3 结构抗震标准的划分Table 3 The division of structural anti－seismic standards

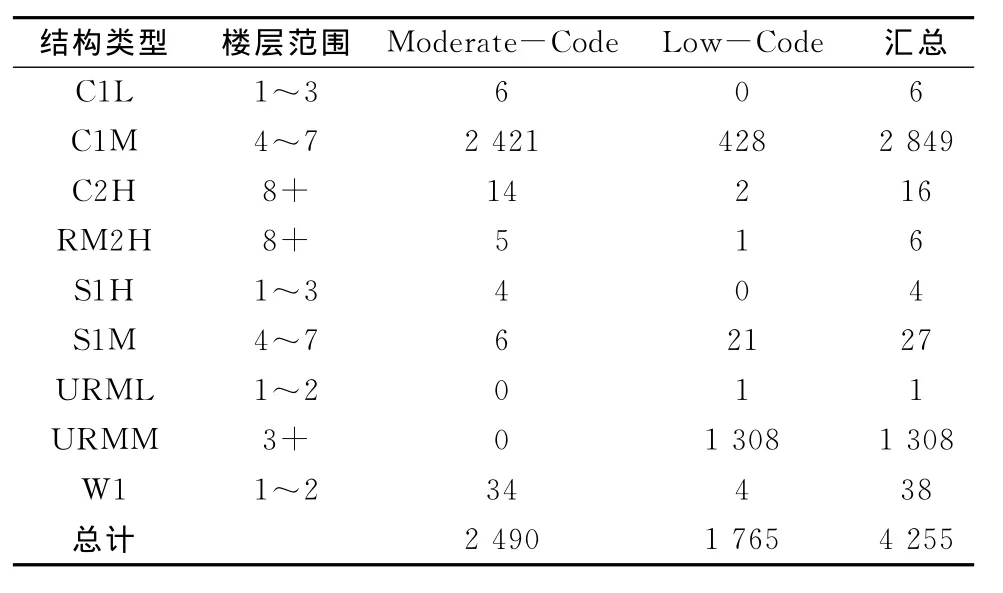
表4 该区域建筑的统计情况Table 4 Building statistics in the region

为了体现本文采用的多自由度集中质量剪切模型的优势，将分别使用本文的多自由度模型方法和传统的单自由度模型方法对该城市进行模拟，单自由度模型的参数根据文献［31］确定。对于这样一个中等城市，多自由度集中质量剪切模型和单自由度模型完成一次地震模拟的计算时间都不到30s，都完全可以满足应急震害预测的速度要求。

计算得到的最大楼层损伤状态的分析结果如图7所示。图中结果显示采用多自由度集中质量剪切模型得到的楼层损伤结果普遍比单自由度模型的预测结果大一些。这是由于多自由度集中质量剪切模型可以得到各个楼层的响应，从而更好的考虑损伤集中现象。对于远场地震波记录和近场无速度脉冲地震动记录，单自由度模型和多自由度集中质量剪切模型的结果差异较小。但是对于近场有脉冲地震动记录，单自由度模型和多自由度集中质量剪切模型的结果具有较大的差别。这是由于速度脉冲能够激励出高阶阵型从而导致结构更加严重的破坏，而单自由度模型无法考虑高阶阵型的影响。

表5 从PEER－NGA数据库中选择的地震动时程记录Table 5 Time－history records of seismic oscillation chose from PEER－NGA database

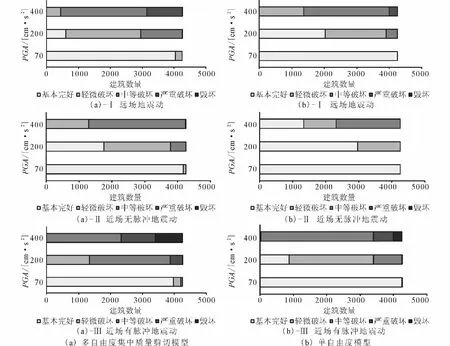
图7 不同模型计算结果的损伤分布情况（5条地震波的平均结果）Fig．7 Damage distribution of computing results of different models（average value of 5earthquake waves）．

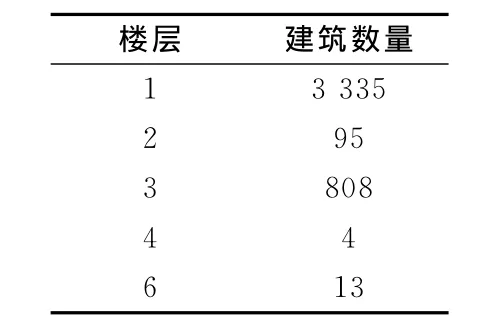
表6 最大损伤（层间位移角）发生的楼层位置Table 6 Floor positions where the maximum damage（drift angle）appears

以峰值加速为200cm／s2的IMPVALL／HBCR＿233地震动为例，采用多自由度集中质量剪切模型得到的最大层间位移角所在楼层如表6所示。建筑破坏的预测结果如图8、9所示。结果显示采用多自由度集中质量剪切模型，能够准确获得建筑损伤的楼层位置和最大加速度位置，显著优于单自由度模型的计算结果。

6 结论

本文详细讨论了基于GPU／CPU协同粗粒度并行计算的区域建筑震害预测方法，得到以下结论：

（1）GPU／CPU协同粗粒度并行计算具有很高的计算效率，其性能价格比能够达到传统CPU计算的39倍。

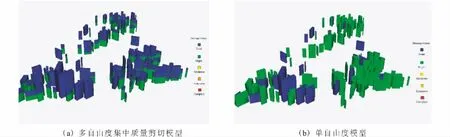
图8 区域中部分建筑各楼层损伤情况 （地震记录：IMPVALL／H－BCR＿233，PGA：200cm／s2）Fig．8 Damage of each floor of some buildings in the region（seismic record：IMPVALL／H－BCR＿233，PGA：200cm／s2）．

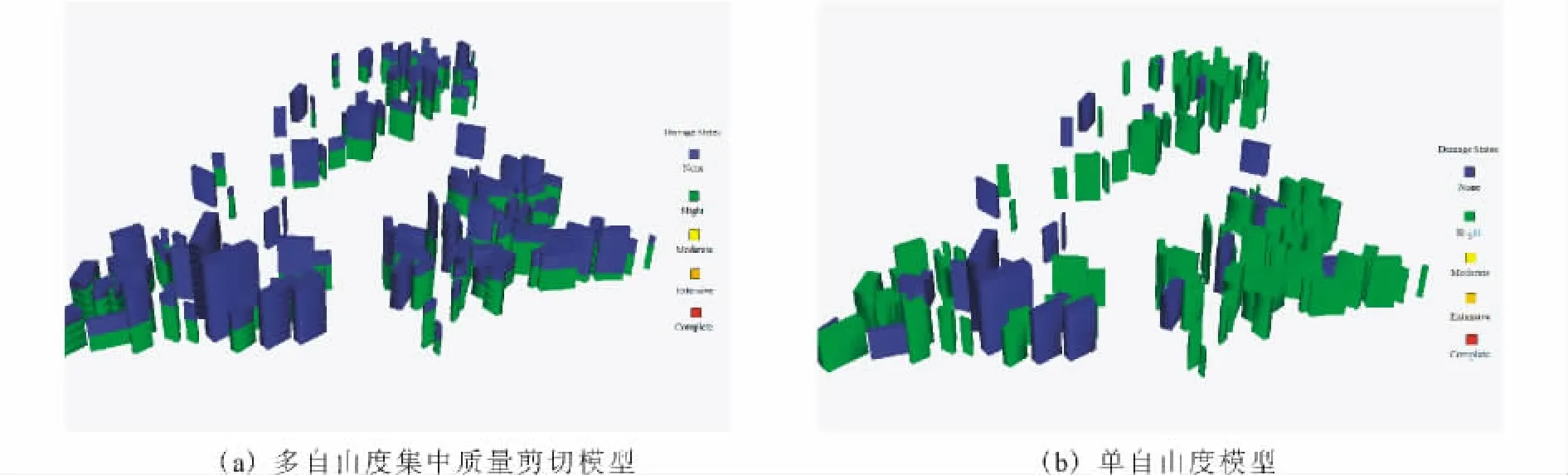
图9 区域中部分建筑各楼层的峰值加速度 （地震记录：IMPVALL／H－BCR＿233，PGA：200cm／s2）Fig．9 Peak acceleration of each floor of some buildings in the region（seismic record：IMPVALL／H－BCR＿233，PGA：200cm／s2）．

（2）根据对比分析的结果，推荐采用单精度计算。

（3）采用的多自由度集中质量剪切模型可以考虑地震动中速度脉冲的影响，也能确定不同楼层的损伤，从而能够更加准确的进行损失预测。

（References）

［1］ Ye L，Lu X，Li Y．Design Objectives and Collapse Prevention for Building Structures in Mega－earthquake ［J］．Earthquake Engineering and Engineering Vibration，2010，9（2）：189－199．

［2］ Onur T，Ventura C E，Finn W D L．A Comparison of Two Regional Seismic Damage Estimation Methodologies［J］．Canadian Journal of Civil Engineering，2006，33（11）：1401－1409．

［3］ Earthquake Loss Estimation Methodology －HAZUS97．Technical Manual ［R］．Washington D C．：Federal Emergency Management Agency－National Institute of Building Sciences，1997．

［4］ Earthquake Loss Estimation Methodology －HAZUS99．Technical Manual ［R］．Washington D C．：Federal Emergency Management Agency － National Institute of Building Sciences，1999．

［5］ Sextos A G，Kappos A J，Stylianidis K C．Computer－aided Pre－and Post－earthquake Assessment of Buildings Involving Database Compilation，GIS Visualization，and Mobile Data Transmission ［J］．Computer－Aided Civil and Infrastructure Engineering，2007，23（1）：59－73．

［6］ Iwan W D．Drift Spectrum：Measure of Demand for Earthquake Ground Motions ［J］．Journal of Structural Engineering，1997，123（4）：397－404．

［7］ Lu X，Lu X Z，Guan H，et al．Collapse Simulation of RC High－rise Building Induced by Extreme Earthquakes［J］．Earthquake Engineering ＆ Structural Dynamics，2012，accepted，DOI：10．1002／eqe．2240．

［8］ Seyedi D M，Gehl P，Douglas J，et al．Development of Seismic Fragility Surfaces for Reinforced Concrete Buildings by Means of Nonlinear Time－history Analysis［J］．Earthquake Engineering ＆ Structural Dynamics，2010，39（1）：91－108．

［9］ Van Nuys Hotel Building Tested Report：Exercising Seismic Performance Assessment［R］．Berkeley，California：Pacific Earthquake Engineering Research（PEER）Center，2005．

［10］ Hori M，Ichimura T．Current State of Integrated Earthquake Simulation for Earthquake Hazard and Disaster［J］．Journal of Seismology，2008，12（2）：307－321．

［11］ Wijerathne M L L，Hori M，Kabeyazawa T，et al．Strengthening of Parallel Computation Performance of Integrated Earthquake Simulation ［J］．Journal of Computing in Civil Engineering，2012．

［12］ Sobhaninejad G，Hori M，Kabeyasawa T．Enhancing Integrated Earthquake Simulation with High Performance Computing［J］．Advances in Engineering Software，2011，42（5）：286－292．

［13］ Owens J D，Luebke D，Govindaraju N，et al．A Survey of General－purpose Computation on Graphics Hardware［C］／／Computer Graphics Forum．［S．l］：Blackwell Publishing Ltd．，2007，26（1）：80－113．

［14］ Stone J E，Phillips J C，Freddolino P L，et al．Accelerating Molecular Modeling Applications with Graphics Processors［J］．Journal of Computational Chemistry，2007，28（16）：2618－2640．

［15］ Weldon M，Maxwell L，Cyca D，et al．A Practical Look at GPU－accelerated FDTD Performance ［J］．ACES Journal－Applied Computational Electromagnetics Society，2010，25（4）：315．

［16］ Lv M H，Wei X，Lei C．A GPU－based Parallel Processing Method for Slope Analysis in Geographical Computation［J］．Advanced Materials Research，2012，538：625－631．

［17］ Che S，Boyer M，Meng J，et al．A Performance Study of General－purpose Applications on Graphics Processors Using CUDA ［J］．Journal of Parallel and Distributed Computing，2008，68（10）：1370－1380．

［18］ Hung S L，Adeli H．A Parallel Genetic／Neural Network Learning Algorithm for MIMD Shared Memory Machines［J］．Neural Networks，IEEE Transactions on，1994，5（6）：900－909．

［19］ Mackerle J．FEM and BEM Parallel Processing：Theory and Applications——A Bibliography （1996－2002）［J］．Engineering Computations，2003，20（4）：436－484．

［20］ Adeli H．High－performance Computing for Large－scale Analysis，Optimization，and Control［J］．Journal of Aerospace Engineering，2000，13（1）：1－10．

［21］ 韩博，陆新征，许镇，等．基于高性能GPU计算的城市建筑群震害模拟［J］．自然灾害学报，2012，21（5）：16－22．

HAN Bo，LU Xinzheng，XU Zhen，LI Yi．Seismic Damage Simulation of Urban Buildings Based on High Performance GPU Computing ［J］．Journal of Natural Disasters，2012，21（5）：16－22．（in Chinese）

［22］ Veletsos A S，Vann W P．Response of Ground－excited Elastoplastic Systems ［J］．Journal of the Structural Division，1971，97（4）：1257－1281．

［23］ Diaz O，Mendoza E，Esteva L．Seismic Ductility Demands Predicted by Alternate Models of Building Frames ［J］．Earthquake Spectra，1994，10（3）：465－487．

［24］ Hajirasouliha I，Doostan A．A Simplified Model for Seismic Response Prediction of Concentrically Braced Frames ［J］．Advances in Engineering Software，2010，41（3）：497－505．

［25］ Multi－hazard Loss Estimation Methodology Earthquake Model HAZUS －MH 2．1Technical Manual［R］．Washington，D．C．：Federal Emergency Management Agency，2012．

［26］ Chopra A K．Dynamics of Structures［M］．Englewood Cliffs，NJ：Prentice Hall，1995．

［27］ Cundumi O，Suárez L E．Numerical Investigation of A Variable Damping Semiactive Device for the Mitigation of the Seismic Response of Adjacent Structures ［J］．Computer－Aided Civil and Infrastructure Engineering，2008，23（4）：291－308．

［28］ NVIDIA CUDA Programming Guide ［Z］．http：／／docs．nvidia．com／cuda／pdf／CUDA＿C＿Programming＿Guide．pdf，2013．

［29］ Lin S B，Xie L L，Gong M S，et al．Performance－based Methodology for Assessing Seismic Vulnerability and Capacity of Buildings［J］．Earthquake Engineering and Engineering Vibration，2010，9（2）：157－165．

［30］ FEMA p695 － quantification of Building Seismic Performance Factors ［R］．Washington D C．：Federal Emergency Management Agency，2009．

［31］ Asteelman J S，Hajjar J F．Influence of Inelastic Seismic Response Modeling on Regional Loss Estimation［J］．Engineering Structures，2009，31（12）：2976－2987．