基于遗传算法与神经网络的水库水沙联合优化调度模型

肖 杨，彭 杨，王太伟

(华北电力大学可再生能源学院，北京 102206)

基于遗传算法与神经网络的水库水沙联合优化调度模型

肖 杨，彭 杨，王太伟

(华北电力大学可再生能源学院，北京 102206)

针对一维泥沙数学模型维数高、求解耗时长以及水沙联合调度模型多目标难以求解的问题，结合遗传算法与神经网络的特性，以发电量最大和有效库容最大为基本目标，构建了水库水沙联合优化调度模型。利用约束法和权重法，将多目标模型转化为单目标模型，采用加速遗传算法进行求解，其中泥沙冲淤量使用自适应BP神经网络进行拟合预测。三峡水库实例计算结果表明:运行20 a，与原设计运行方式相比，采用该优化调度模型优化运行年均发电量增加7.732%，泥沙淤积量增加0.044%，在淤积量增加很小的情况下能大幅度增加发电量，模型能较好地解决水库水沙联合调度问题，在工程实际中是有效可行的。

水沙联合优化调度;加速遗传算法;自适应BP神经网络;三峡水库

水库的水沙调控是协调水库短期效益和长期效益、局部效益和整体效益的有效途径，在发挥水库长期综合效益中具有重要作用。在以往的研究中，水库调度通常是对水流进行调节，很少考虑泥沙问题。水沙联合调度涉及水库优化调度和水库泥沙淤积与排沙调度，由于水量调度与泥沙冲淤性质不同，时间尺度难以匹配，目前对水库水沙联合优化调度的研究并不多。早期张玉新等［1］运用多目标决策方法，以水库调度周期内发电量最大和泥沙淤积量最小为基本目标，建立了水沙联合调度多目标动态规划模型;之后彭杨等［2］考虑水库的防洪、发电、航运等多目标运用，建立了水库水沙联合调度多目标决策模型;练继建等［3］将遗传算法和神经网络应用于水沙联合调度的研究中;王帅等［4］运用改进的POA算法对水沙联合调度多目标规划模型进行了研究。以上研究从不同方面对水沙联合调度问题进行了论述，由于水库运用的多目标特性和水沙联合调度求解的复杂性，对该问题还需要做进一步研究。本文兼顾水库的防洪、发电、航运、长期利用及补水等多目标要求，建立水库水沙联合优化调度模型，并应用加速遗传算法结合自适应BP神经网络对其进行求解，最后将该模型和求解方法应用于三峡水库长期运行研究中。

1 水库水沙联合优化调度模型

1.1 多目标模型

水库通常具有防洪、发电、航运、长期利用、供水等综合运用功能。防洪要求汛期水库水位降至水库安全水位且下泄流量达到下游防洪安全的要求;发电是在保证水库下游安全的情况下尽可能多发电;航运要求水位达到通航保证的要求;长期利用要求水库的淤积量尽量小;供水要求水库必须满足流域区域的灌溉、生产生活用水和生态环境的需求［5-6］。防洪、航运、供水的要求和效益的发挥可通过水库运行水位和下泄流量的约束条件来满足，在满足约束条件下优化水库发电效益和实现长期利用成为水库综合利用的关键，其目标体现为发电量最大和有效库容最大:

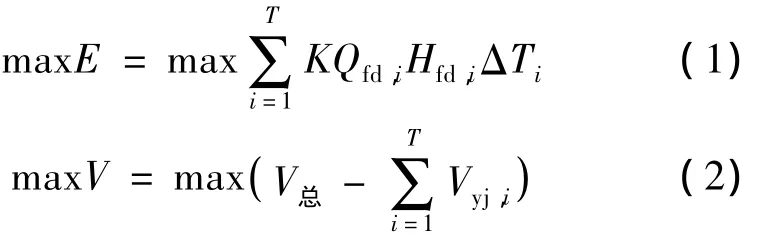
式中:E为发电量;K为出力系数;i为计算时段;T为计算期内总时段数;Qfd，i为时段发电流量;Hfd，i为发电水头;ΔTi为计算时段长度;V为有效库容;V总为水库总库容;Vyj，i为时段泥沙淤积量。

1.2 单目标模型

水库水沙联合优化调度由水库发电调度与泥沙冲淤计算组成，由于防洪安全的需要，汛期水库一般水位较低，发电量较少，而排沙显著，所以汛期将库区排沙作为主要目标;非汛期来流量相对较小，含沙量低，水库蓄水高水位运行，库区泥沙淤积较少，发电占主导地位。将发电量与淤积量转化为经济指标，再利用权重法，分汛期和非汛期赋予发电效益与淤积损失各自的权重，采用线性加权原理，把多目标模型转化为单目标模型进行求解，构建的目标函数为式中:F(j)为发电量最大与淤积量最小的综合效益函数;j为库容系列;λ1、λ2分别为发电效益和泥沙淤积损失的权重;f(Eij)为把发电量换算为经济指标的函数;g(Vyj，ij)为把泥沙淤积量换算为经济损失指标的函数;Eij为 i时段 j系列发电量;Vyj，ij为 i时段j系列泥沙淤积量。

1.3 约束条件

a.水库特性约束:

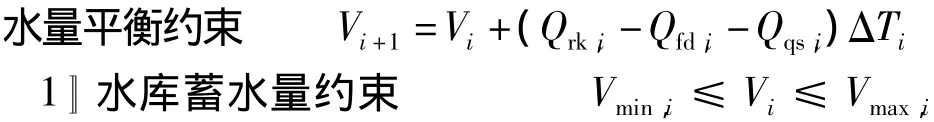
式中:Vi为i时段末库容;Qrk，i为i时段的入库流量;Qqs，i为 i时段弃水量;Vmax，i为 i时段水库允许的最大蓄水库容，汛期为防洪库容，非汛期为正常蓄水位对应库容;Vmin，i为i时段水库最小蓄水库容，通常为死水位对应的库容。

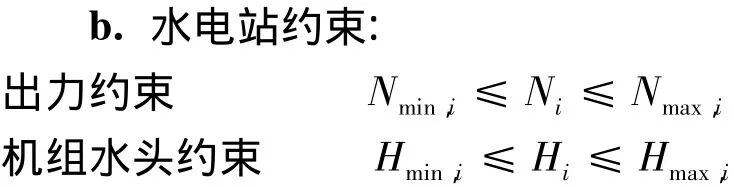
式中:Ni为第i时段的出力;Nmin，i为第i时段的保证出力;Nmax，i为第i时段的最大出力;Hi为第i时段的水头;Hmin，i、Hmax，i分别为机组允许的最小、最大水头。

式中:Zi为水库运行水位;Zfh，i为汛期防洪限制水位;Zhy，i为库区航运保证水位;Qxy，i为水库下泄流量;Qmaxfh，i为水库防洪允许下泄最大流量;Qminfh，i为水库下游航运保证流量或要求下泄最小流量;Qminbs，i为下游补水需要下泄的最小流量。

d.非负约束:以上各种变量均为非负值。

2 模型求解

由于遗传算法具有广泛的适用性与扩展性、全局优化等优点，特别适用于求解大规模复杂性的多维非线性优化问题，但也存在着收敛较慢、局部搜索能力较弱等不足［7-9］，所以本文结合已有研究成果［10-12］，采用实数编码的加速遗传算法(RAGA)［13］来求解建立的水库水沙联合优化调度模型。将整个调度期水库各时段末库容系列作为基本的种群个体，将目标函数式(3)作为适应度函数，经过加速遗传运算获得效益最大的个体，其对应的出流量过程作为水库的最佳运行方式。其中，泥沙淤积量采用已训练好的自适应BP神经网络进行预测计算:来水量、来沙量已知，根据水量平衡方程、上游水位-库容曲线和下游水位-下泄流量曲线，由随机生成的库容序列，即可得到水库运用水位和下泄流量，从而进行泥沙淤积的自适应BP神经网络快速预测。

2.1 基于自适应BP神经网络的泥沙冲淤计算

由文献［14-15］可知，水库的泥沙冲淤计算可根据一维水沙数学模型进行求解，但在水沙优化计算中，每次得到新的水位、流量都要代入水沙数学模型的计算程序之中，而水量的调度过程与泥沙的冲淤计算过程本身就比较复杂，因此迭代运算十分复杂，且效率很低。由于人工神经网络的非线性映射能力能够很好地反映水沙调度中多个自变量和因变量之间的复杂关系，具有较高的模拟精度和较好的可行性，且应用简便［16-18］，所以能很好地模拟预测水库运行时的泥沙淤积量。为了缩短计算泥沙淤积量的时间，利用自适应BP神经网络(A-BP神经网络)拟合一维水沙数学模型计算成果进行泥沙的冲淤模拟计算。

A-BP神经网络计算步骤［13，18］如图1 所示。结合水库水沙联合优化调度单目标模型，A-BP神经网络模拟预测泥沙淤积量需要输入的样本数据包括入库流量 Qrk，ij、入库水流含沙量 Srk，ij、时段水头 Hij、下泄流量Qxy，ij。泥沙淤积量的求解公式为

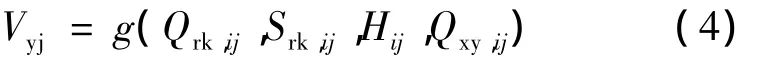
式中:g(Qrk，ij，Srk，ij，Hij，Qxy，ij)为利用 A-BP 神经网络拟合预测泥沙淤积量的函数。

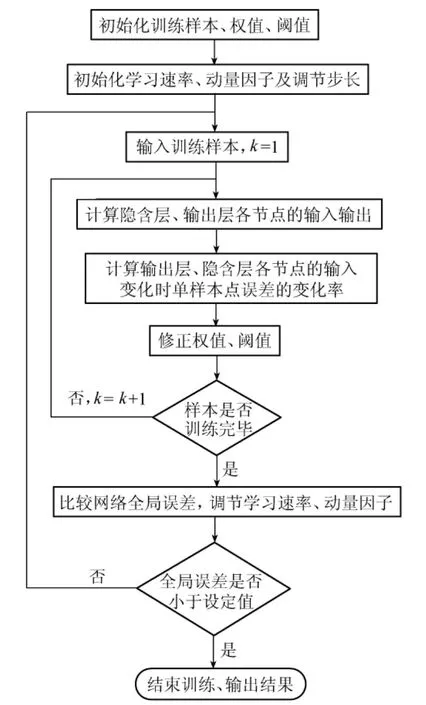
图1 A-BP神经网络计算流程

利用A-BP神经网络对一维水沙数学模型计算结果进行拟合训练，结果如图2所示，拟合最大误差为4.139%，平均误差仅为0.343%，拟合效果较好。

2.2 水库水沙联合优化调度模型的加速遗传算法求解步骤

本文采用加速遗传算法来求解水库水沙联合优化调度模型，其计算步骤如下:

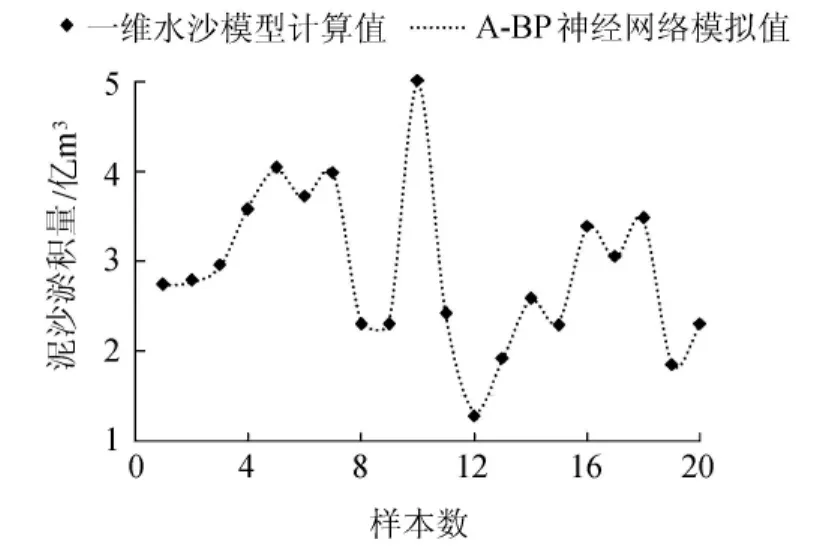
图2 A-BP神经网络对一维水沙数学模型计算结果的拟合训练

a.编码。采用实数编码，以时段末库容值Vij作为优化变量，即以各时段末库容值为“基因”，以整个调度期各时段末库容系列为“染色体”。

b.种群初始化。在库容约束范围内随机生成M组库容系列作为初始种群，即:V11，V21，…，VT1;V12，V22，…，VT2;…;V1M，V2M，…，VTM。而后对初始种群(即父代群体)采用式(5)进行初始化。

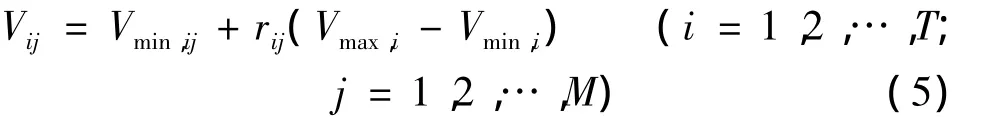
式中:rij为［0，1］内生成的均匀分布随机数;M为种群规模。

c.适应度计算。将目标函数值作为个体的适应度，分别利用式(1)计算发电量、利用A-BP神经网络按式(4)计算泥沙淤积量，最后按式(3)计算满足约束条件下的第j个库容系列的适应度值。

d.选择。由适应度值计算每个个体被选择的概率Pj，然后得到染色体Xi的累计概率qi，Pj与qi的表达式分别为

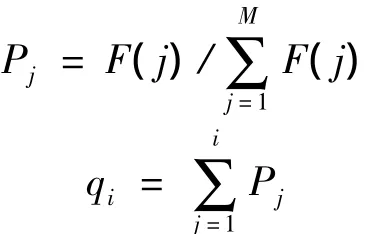
在［0，1］内生成均匀分布的随机数 r，若 r≤q1，则染色体 X1被选中;若 qi－1≤r≤qi，则染色体 Xi被选中，其中 i=2，3，…，T。

e.交叉。由均匀分布随机选择策略选择交叉父代，以交叉概率Pc确定交叉个体数nc，随机选择两个个体 x1l、x2l(l=1，2，…，nc)作为双亲，采用式(5)进行随机线性组合，产生交叉后的子代个体x'1l、x'2l:

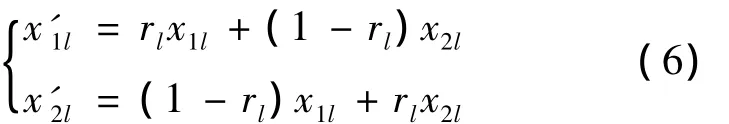
式中:rl为［0，1］内生成的均匀分布随机数。

f.变异。确定变异概率Pm，在种群中按均匀分布随机选取染色体xl(l=1，2，…，nm，其中nm为变异个体数)，利用式(6)对个体xl进行变异，产生变异后的新个体x'l。

式中:u(xl)为变异函数。

g.演化迭代。由步骤c～f得到交叉变异后的种群，按照其适应度值从大到小排列，取前M个个体作为新的父代群体，然后转入步骤c，重新对新的父代群体进行评价、选择、交叉和变异，如此循环。

h.加速循环。根据对遗传算法的选择、交叉、变异寻优性能的分析，用前两次演化迭代生成的优秀个体所对应的变量变化区间作为变量新的初始变化区间，然后转入步骤a，如此加速循环［13］，直至最优个体的目标函数值达到收敛准则或达到预定加速循环次数，输出当前群体中最佳个体或优秀个体的平均值作为实数编码的加速遗传算法的计算结果。

以上即为水库水沙联合优化调度实数编码的加速遗传算法完整计算步骤，可通过Fortran语言编程来实现以上步骤的数值计算。

3 实例分析

三峡水库是集防洪、发电、航运、排沙、补水等效益为一体的多目标特大型水利工程［19-20］，设计正常蓄水位175 m，相应库容393亿m3，枯水期消落低水位155m，防洪限制水位145m，防洪库容221.5亿m3，保证出力530万kW，最大出力2250万kW，枯水期平均调节流量5860m3/s。三峡水库设计为“蓄清排浑”方式运用［21］，即汛期来沙多时降低水位排沙，非汛期来沙少时蓄水兴利。

选取三峡水库1971—1990年的实际来水来沙资料进行模拟计算，以旬为时段长度，种群组数M选为50，初始交叉概率 Pc、变异概率 Pm分别为0.85和0.02，防洪下泄流量设为5.5万m3/s。汛期以排沙为主，取λ1、λ2分别为0.3和0.7;非汛期以发电为主，取λ1、λ2分别为0.7和0.3。结合三峡水库的上游水位-库容关系曲线、下游水位-下泄流量曲线及已知的其他资料进行优化计算。

计算结果如表1所示，与原设计运行方式相比，三峡水库采用加速遗传算法优化运行20 a，年均发电量为838.176亿kW·h，相对原设计运行方式下的778.021亿kW·h增加7.732%;而库区泥沙累积淤积量为59.115亿m3，仅增加0.044%;调节库容保留率为97.168%，相对原设计运行方式下的97.169%基本没有变化;年均综合效益188.368亿元，增加9.047%，计算结果与文献［21］的论证结果一致。对于汛期和非汛期，发电效益和库区泥沙冲淤效益选取不同的权重，使得汛期排沙占主要地位，大流量下适当降低水位能更加高效地排沙;非汛期发电占主要地位，适时适当地抬高运行水位，能大幅增加发电量，这与三峡水库的“蓄清排浑”运用方式一致。这样能确保全年发电量增加明显，而淤积量基本没有增加。这充分说明该模型和求解方法能有效模拟计算三峡水库较优的综合效益运行方式。

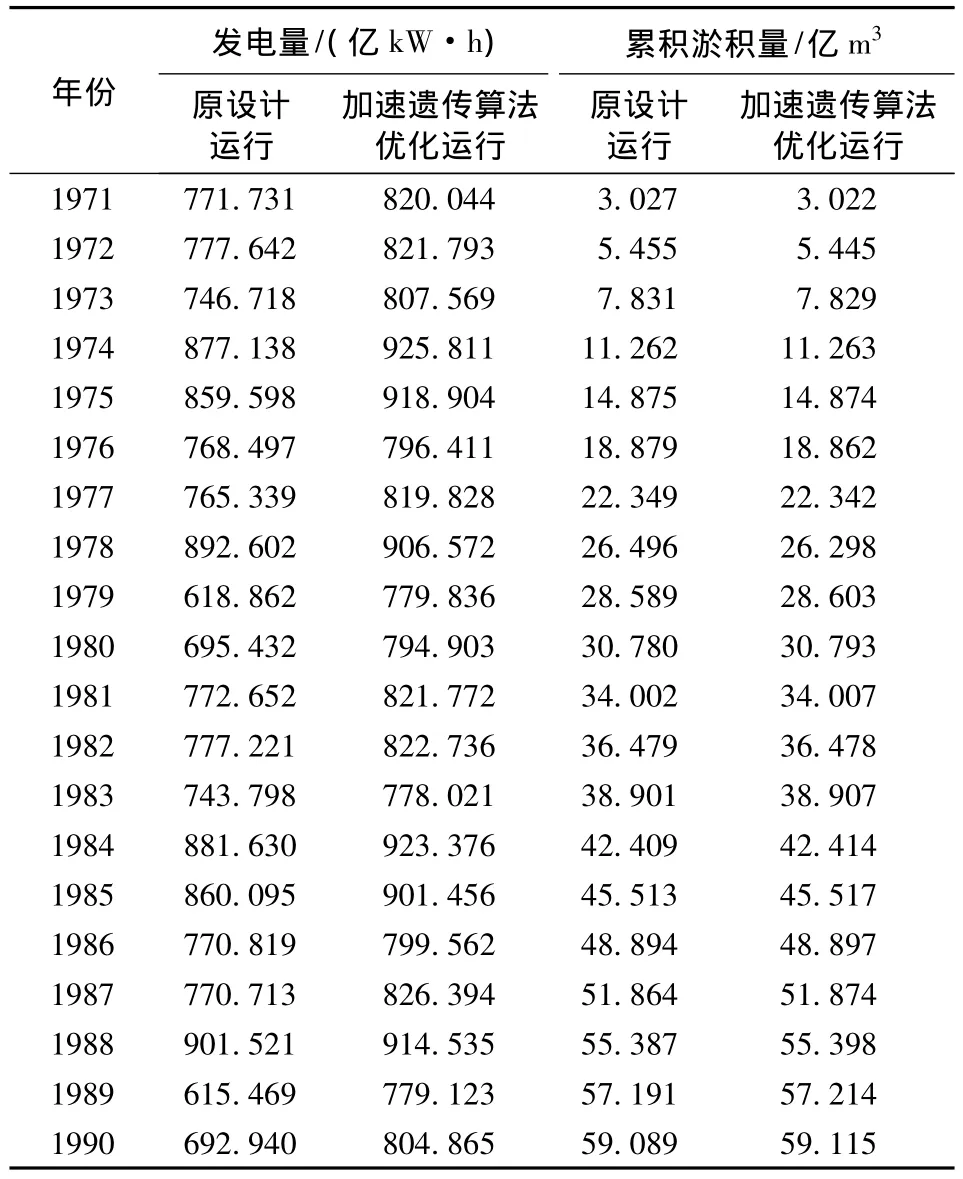
表1 三峡水库不同运行方式下发电量和泥沙累积淤积量对比

4 结语

实数编码的加速遗传算法可以避免过早收敛，提高运算效率，加快算法的收敛速度，能有效地解决水库水沙联合优化调度问题。利用自适应BP神经网络对泥沙淤积量进行非线性回归拟合，避免了在优化调度模型求解时的繁琐计算。通过对三峡水库水沙联合优化调度的运算表明，利用加速遗传算法和自适应BP神经网络来计算模拟水沙联合优化调度是有效可行的。

随着三峡水库的多目标综合利用要求的提高，尤其是近年来三峡水库对流域干旱的补水、生态环境效益调度等逐渐展开，如何集三峡水库的防洪、发电、航运、排沙、补水、生态环境等综合效益为一体进行系统的优化调度，有待进一步研究。

［1］张玉新，冯尚友.水库水沙联调的多目标规划模型及其应用研究［J］.水利学报，1988(9):19-26.(ZHANG Yuxin，FENG Shangyou.Multi-objective programming model in reservoir operation and its application［J］.Journal of Hydraulic Engineering，1988(9):19-26.(in Chinese))

［2］彭杨，李义天，张红武.水库水沙联合调度多目标决策模型［J］.水利学报，2004(4):1-7.(PENG Yang，LI Yitian，ZHANG Hongwu.Multi-objective decision-making model for coordinative dispatch of water and sediment in reservoir［J］.Journal of Hydraulic Engineering，2004(4):1-7.(in Chinese))

［3］练继建，胡明罡，刘媛媛.多沙河流水库水沙联调多目标规划研究［J］.水力发电学报，2004，23(2):12-16.(LIAN Jijian，HU Minggang，LIU Yuanyuan.Research of multi-objective operation of water and sand in reservoir on sandy river［J］.Journal of Hydroelectric Engineering，2004，23(2):12-16.(in Chinese))

［4］王帅，彭杨，刘方，等.POA算法在水库水沙联合调度中的应用研究［J］.水电能源科学，2012，30(4):29-31.(WANG Shuai，PENG Yang，LIU Fang，et al.Application of progressive optimality algorithm to reservoir watersediment joint regulation［J］.Water Resources Power，2012，30(4):29-31.(in Chinese))

［5］宋刚福，沈冰.基于生态的城市河流水量水质联合调度模型［J］.河海大学学报:自然科学版，2012，40(3):258-263.(SONG Gangfu，SHEN Bing.An ecology-based water quantity and quality combined operation model for urban rivers［J］.Journal of Hohai University:Natural Sciences，2012，40(3):258-263.(in Chinese))

［6］张松达，苏飞，夏梦河.考虑水质的水资源调配模型及其解法［J］.河海大学学报:自然科学版，2010，38(6):620-624.(ZHANG Songda，SU Fei，XIA Menghe.Water resources allocation and operation model considering water quality demand and its solution［J］.Journal of Hohai University:Natural Sciences，2010，38(6):620-624.(in Chinese))

［7］吴学文，索丽生，王志坚.水电站水库优化调度的改进混沌遗传算法［J］.水利水电科技进展，2010，30(2):53-57.(WU Xuewen，SUO Lisheng，WANG Zhijian.Improved chaotic genetic algorithm for optimal operation of hydropower reservoirs［J］.Advances in Science and Technology of Water Resources，2010，30(2):53-57.(in Chinese))

［8］魏加华，张远东.基于多目标遗传算法的巨型水库群发电优化调度［J］.地学前缘，2010，17(6):255-262.(WEI Jiahua，ZHANG Yuandong.Optimal operations of multi-reservoir system using multi-objective genetic algorithms［J］.Earth Science Frontiers，2010，17(6):255-262.(in Chinese))

［9］游进军，纪昌明，付湘.基于遗传算法的多目标问题求解方法［J］.水利学报，2003(7):64-69.(YOU Jinjun，JI Changming，FU Xiang.New method for solving multiobjective problem based on genetic algorithm［J］.Journal of Hydraulic Engineering，2003(7):64-69.(in Chinese))

［10］HAKIMI-ASIABAR M，GHODSYPOUR S H，KERACHIAN R.Deriving operating policies for multi-objective reservoir systems:application of self-learning genetic algorithm［J］.Applied Soft Computing，2010(10):1151-1163.

［11］吴成国，王义民，黄强，等.基于加速遗传算法的梯级水电站联合优化调度研究［J］.水力发电学报，2011，30(6):171-177.(WU Chengguo，WANG Yimin，HUANG Qiang，et al.Study on combined optimal operation of cascade hydropower stations based on accelerating genetic algorithm［J］.Journal of Hydroelectric Engineering，2011，30(6):171-177.(in Chinese))

［12］万星，周建中.自适应对称调和遗传算法在水库中长期发电调度中的应用［J］.水科学进展，2007，18(4):598-603.(WAN Xing，ZHOU Jianzhong.Application of genetic algorithm for self adaptation，symmetry and congruity in reservoirmid-long hydraulic power operation［J］.Advances in Water Science，2007，18(4):598-603.(in Chinese))

［13］朝伦巴根，贾德彬.数值计算方法［M］.2版.北京:中国水利水电出版社，2011.

［14］李义天，孙昭华，邓金运，等.长江水沙调控理论及应用［M］.北京:科学出版社，2011.

［15］包为民，万新宇，荆艳东.多沙水库水沙联合调度模型研究［J］.水力发电学报，2007，26(6):101-105.(BAO Weimin，WAN Xinyu，JING Yandong.Study on joint scheduling model of water and sediment in sediment-laden reservoir［J］.Journal of Hydroelectric Engineering，2007，26(6):101-105.(in Chinese))

［16］苑希民，李鸿雁，刘树坤，等.神经网络和遗传算法在水科学领域的应用［M］.北京:中国水利水电出版社，2002.

［17］刘媛媛，练继建.遗传算法改进的BP神经网络对汛期三门峡水库泥沙冲淤量的计算［J］.水力发电学报，2005，24(4):110-113.(LIU Yuanyuan，LIAN Jijian.Calculation of sediment and scour of Sanmenxia reservoir in flood season by the BP neural network improved by GA［J］.Journal of Hydroelectric Engineering，2005，24(4):110-113.(in Chinese))

［18］翟宜峰，李鸿雁，刘寒冰.人工神经网络与遗传算法在多泥沙洪水预报中的应用［J］.泥沙研究，2003(2):7-13.(ZHAI Yifeng，LI Hongyan，LIU Hanbing.Application of artificial neural networks and genetic algorithms on siltladen flood forecasting［J］.Journal of Sediment Research，2003(2):7-13.(in Chinese))

［19］陆佑楣，曹广晶，等.长江三峡工程:技术篇［M］.北京:中国水利水电出版社，2010.

［20］邵东国，邵学军，陆永军，等.长江流域水沙生态综合管理［M］.北京:科学出版社，2009.

［21］中国工程院三峡工程阶段性评估项目组.三峡工程阶段性评估报告:综合卷［M］.北京:中国水利水电出版社，2010.

Water-sediment coordinated optimized dispatch model of reservoir based on genetic algorithm and neural

network

XIAO Yang，PENG Yang，WANG Taiwei(School of Renewable Energy，North China Electric Power University，Beijing 102206，China)

In order to solve problems including multi-dimensions and long solution times of a one-dimensional sediment model，multi-objectives and the solution difficulty of a water-sediment coordinative dispatch model，a water-sediment coordinated optimized dispatch model was established on the basis of characteristics of genetic algorithms and neural networks.The model took the maximum power generation and effective storage as the elementary objects.The multiobjective model can be transformed into a single-objective model with the method of restricting and weighting.The singleobjective model is solved using the method of accelerating genetic algorithm.The adaptive BP neural network was used to fit the prediction for the sedimentation and scour.Three Gorges Reservoir case results show that the average annual electric energy production and the sedimentation and scour increase by 7.732%and 0.044%，respectively，compared to those of the original design after the project operated for 20 years.The power generation can be markedly increased in the case of little sedimentation and scour.The model can solve water-sediment coordinative optimized dispatch well and is also effective in engineering practice.

water-sediment coordinative optimized dispatch;accelerating genetic algorithm;adaptive BP neural network;Three Gorges Reservoir

TV145

A

1006-7647(2013)02-0009-05

10.3880/j.issn.1006-7647.2013.02.003

国家自然科学基金(51179069)

肖杨(1986—)，男，河南固始人，硕士研究生，主要从事水沙运动模拟与调控方法研究。E-mail:xiaoyang5806@126.com

2012-05-29 编辑:熊水斌)