基于奇异点检测的行波单端测距方法研究
2013-09-05孟凡铮王喜疆
孟凡铮,王喜疆
(1.新疆电力公司检修公司,新疆 乌鲁木齐 830000;2.新疆新能物资有限公司,新疆 乌鲁木齐 830000)
0 引言
传统故障测距是基于工频电气量,其中工频阻抗法是广泛应用的方法。它以线路集中参数模型为基础,测距精度受故障点的过渡电阻、系统运行阻抗、负荷电流等因素的影响,误差较大,测距精度无法保证[1]。但基于行波法的故障定位,在理论上不受线路类型及过渡电阻的影响[2]。原理简单,也不受系统通信技术条件的限制。相比单端测距,双端测距可靠性高,但对通信精度要求高,大大增加了成本。因此,单端测距成为研究的一个热点[3]。在简要介绍故障行波基本概念的基础上,利用单端测距,基于奇异点模极大值检测的方法分析暂态过程中的电气量,对故障定位进行了探讨。
1 故障暂态行波在输电线路的传输
当线路上某一点发生故障时,可用叠加原理将其分解为正常负荷分量和故障分量二者的叠加,故障分量相当于在系统电势为零时在故障点加一个与正常负荷大小相等、方向相反的电压,在这一电压下,将会产生由故障点向线路两端传播的波形。如图1所示,F点故障时,将由故障点向两端传播行波。
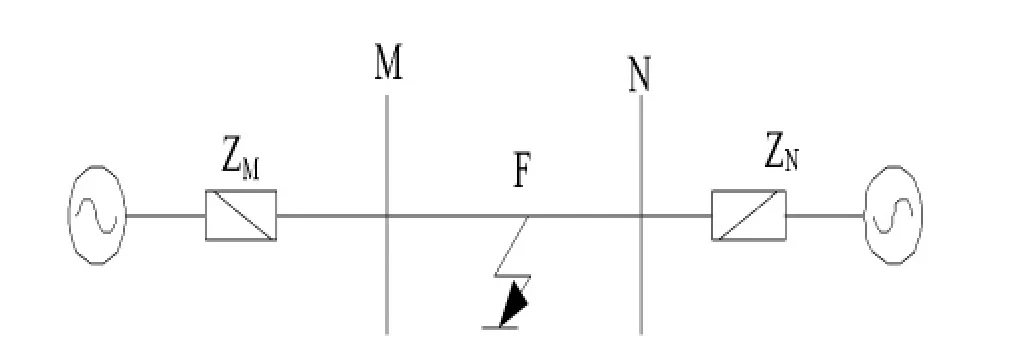
图1 单根无损行波
如果将单根无损的分布参数线路上的电压u和电流i用在线路上的位置x和时间t为变数的偏微分方程来表示,则

其中,L、C为线路单位长度的电感和电容。
将其分别对x和t微分,经变换可得到波动方程

则其达朗贝尔解为

式中,u1()为x正方向行波;u2()为x反方向行波;v=是波速;Zc=,是波阻抗。

图2 仿真模型
2 输电线路故障行波的提取
对模型进行故障仿真后,提取三相电压和电流的暂态量,由于各相之间存在耦合,每相包含的行波分量并不孤立,所以要把互不独立的相分量转换成独立的模分量。利用模量行波实现相应功能,相模变换通过Clarke变换则有
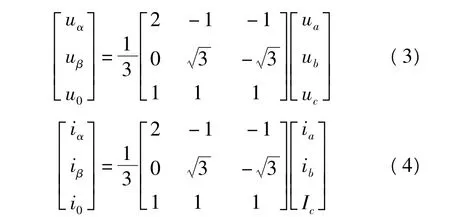
式中,ua、ub、uc分为三相电压行波分量;uα、uβ、u0分别为电压行波的α、β、0模分量;i为相应的电流分量。
因此,方向行波的模量可表示为

式中,S1α、S1β、S10为正向行波的 α、β、0 模分量;S2α、S2β、S20为反向行波分量;Zα、Zβ、Z0为相应的波阻抗。
3 小波变换及模极大值
对提取的行波信号进行多尺度分析,在信号出现突变时,其小波变换后的系数具有模极大值,因而可以通过对模极大值点的检测来确定故障发生的时间点。首先给出小波变换模极大值的定义。设WSf(x)(s=2j)是函数f(x)的小波变换,在尺度 s下,在 x0的某一邻域 δ,对一切 x有:WSf(x)≤WSf(x0),则称x0为小波变换的模极大值点,WSf(x0)为小波变换的模极大值。小波变换的模极大值点与信号的突变点是一一对应的。若函数f(x)(f(x)єR)在某处间断或某阶导数不连续,则称该函数在此处有奇异性;若函数f(x)在其定义域有无限次导数,则称f(x)是光滑的或没有奇异性。一个突变的信号在其突变点必然是奇异的,因而可以通过对奇异的点的检测来确定故障发生的时间点。
4 建模与仿真
4.1 仿真模型
基于以上数学理论在Matlab中搭建仿真模型如图2所示,设置仿真时间为0.0~0.10 s,采用步长Ode23tb算法,设置A相短路,故障点距离测量点80 km,短路时间为[0.035 0.100]。
4.2 仿真结果
算例仿真后,三相电压电流波形如图3、4所示。
通过检测点的三相电流和电压的波形可以看出,仿真后的电压、电流波形符合线路发生A相短路故障的特征,从而说明了仿真模型的正确性。
4.3 故障点行波提取
在Matlab中用语言将算法写成程序,利用式(3)、式(4)把电流电压的暂态量进行Clarke变换得到相应的模分量,再利用式(5)、式(6)计算正向、反向行波的模分量,如图5所示。
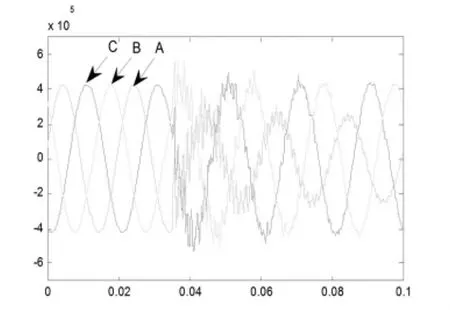
图3 检测点三相电压波形

图4 检测点三相电流波形
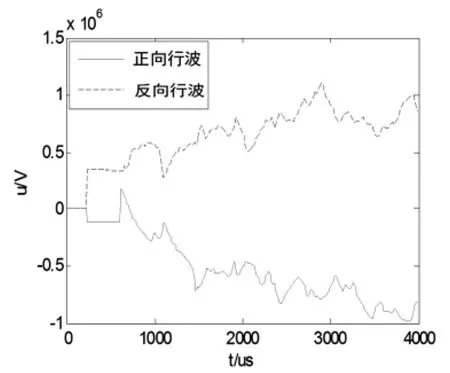
图5 电压α模正向和反向行波
故障后行波第一个波头突变都比较明显,以后进入母线、变压器后经过折反射后出现明显的畸变和衰减。利用电压行波较电流行波有一定的优势:系统阻抗较大时,电压行波幅值相对电流行波较大,易于测量;电压行波较电流行波灵敏度高[4]。这也是选择以电压行波为测量对象的原因。
4.4 基于奇异点模极大值的小波变换
在Matlab中编程,用小波对信号进行6层分解,如图6、图7所示。由于反向行波进行检测可有效屏蔽由非故障线路折射过来的波头,所以选取反向电压行波为原始信号,对信号进行多尺度分析,在信号突变时其小波变换后的系数具有模极大值,因而可以通过模极大值点的检测来确定故障发生的时间点,从图6经过小波分解后的第1个波头的时间点为28 ms,故障点第2个反射波时间点为83 ms,通过单端测距公式求得故障距离测量点80.46 km。
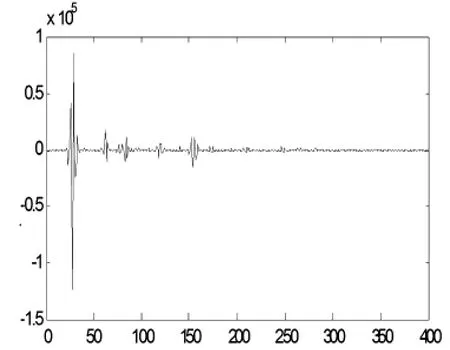
图6 反向行波的小波变换
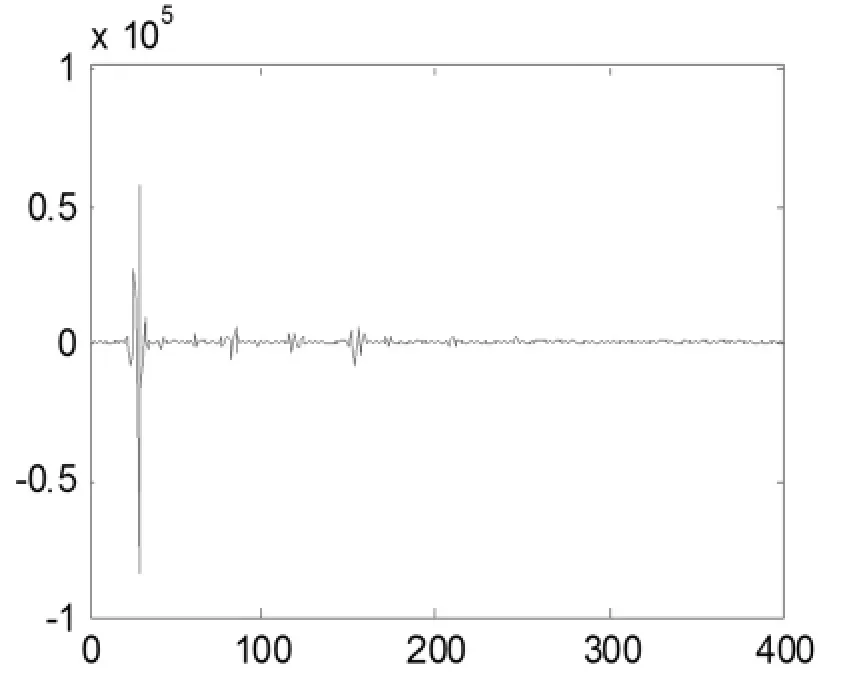
图7 接地电阻为100 Ω反向行波的小波变换
当存在接地电阻时,对测距精度影响不大,测距结果均为80.46 km。但与金属性接地故障相比信号微弱,比较图6与图7可明显看出当接地电阻为100 Ω时,经变换后的行波模极大值远小于金属性接地故障,而对故障发生的时间点无任何影响。
4.5 不同母线类型的验证
母线连接的方式主要有两种:一种是母线上除了故障线路外没有其他出线,另一种是有其他出线,这两种母线的主要差别是暂态行波反射系数不同。故选取3个双电源模型系统,验证故障发生与不同位置、不同短路故障类型的定位效果。第1个模型如图7所示,其中MN=100 km;第2个模型如图8所示,其中MN=100 km,RM=50 km;第3个模型如图5~8所示其中 RM=50 km,MN=100 km,NS=30 km。电压等级为500 kV,两端电压夹角30°。

表1 不同模型的测距结果
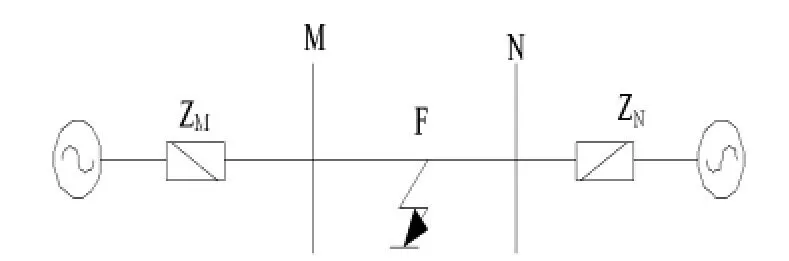
图8 仿真模型1
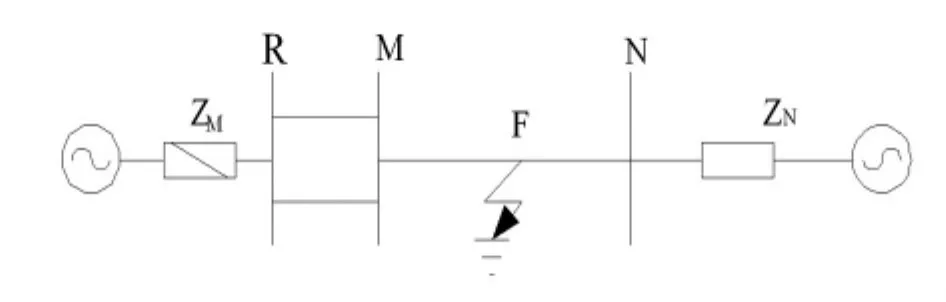
图9 仿真模型2
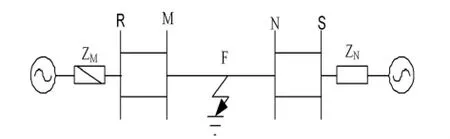
图10 仿真模型3
5 结论
为了验证算法的有效性,建立了3种仿真模型,表1给出了接地故障发生在不同位置、不同接地电阻的定位效果。3种测距结果显示,这种方法能够实现精确定位,最大误差为2.4%,能够满足单端测距的要求。大量仿真表明行波测距精度受过渡电阻影响不大,过渡电阻只改变其幅值,对精度的影响有限。
[1]葛耀中.新型继电保护和故障测距的原理与技术(第二版)[M].西安:西安交通大学出版社,2007.
[2]李幼仪,董新洲,孙元章.基于电流行波的输电线路横差保护[J].中国电机工程学报,2002,22(11):6-10.
[3]康小宁,索南加乐.基于参数识别的单端电气量频域法的故障测距原理[J].中国电机工程学报,2005,32(1):22-27.
[4]王志华.超高压输电线路故障行波定位及高压变频技术研究[D].武汉:华中科技大学,2004.
[5]高淑萍,索南加乐.基于分布参数模型的直流输电线路故障测距方法[J].中国电机工程学报,2010,30(13):75-79.
[6]徐青山,陈锦根,唐国庆.考虑母 线分布电容影响的单端行波测距法[J].电力系统自动化,2007,31(2):70-73.
[7]王志华.超高压输电线路故障行波定位及高压变频技术研究[D].武汉:华中科技大学,2004.
[8]施慎行,董新洲,周双喜.单相接地故障行波分析[J].电力系统自动化,2005,29(23):29-32,53.
