输电线路直流融冰时间的计算和试验验证

范松海，刘 馨，聂鸿宇，刘 睿

(四川电力科学研究院，四川 成都 610072)

自上个世纪50年代电网冰灾频发以来，很多专家、学者以及公司对输电线路融冰进行了专门研究，建立了许多融冰时间的计算模型。归纳起来，融冰模型可以大致分为两大类:一是融冰静态模型。此类模型没有考虑到融冰过程中状态的不断改变对融冰的影响，把融冰过程等效成一个静止不变的过程，以此为基础建立融冰模型［1］。但是，目前已有的融冰模型均没有考虑到融冰过程中热量动态交换过程，因而计算结果与实际情况误差较大。

吸收了文献［1-5］的一些合理因素，把融冰问题看成是一个移动界面问题(Stefan问题)，同时摒弃了文献［1-5］中与实际情况不符的一些假设条件，因而得到了不同于文献［1-5］的融冰过程。例如，文献［1-5］认为，在融冰过程中，逐渐扩大的冰层内表面始终是与导线外表面同心的圆。因为考虑了冰层因重力作用下移这一物理过程，冰层内表面随冰层一起下移，使其呈椭圆形状不断扩大。模型的计算结果与人工气候室中直流融冰试验的结果基本相符。

1 导线融冰模型及其计算过程

1.1 焦耳热融冰的物理数学模型

由于冰层重力矩的作用，导线在覆冰过程中会发生扭转，从而使冰层呈均匀的圆柱状。在融冰过程中，融冰水经冰层空隙流失，冰和导线之间形成气隙。大量试验结果表明，当导线上的冰层呈均匀的圆柱形且厚度小于导线直径时，气隙(包括导线)的截面形状接近于椭圆形，如图1(a)所示。当导线足够长且覆冰均匀时，导线沿轴向的传热可以忽略不计。因而，通电导线的融冰模型可以简化为截面上的二维传热模型，如图1(b)所示。利用焦耳热融冰的传热过程发生在以下5个区域:Θ1为导线钢芯;Θ2为导线铝层;Θ3为气隙;Θ4为冰层;Θ5为环境。5个区域由4个界面分开:导线钢芯-导线铝层(Θ1-Θ2)、导线 -气隙(Θ2-Θ3)、气隙 -冰层(Θ3-Θ4)、冰层-环境(Θ4-Θ5)。

图1 融冰导线的横截面

热量由导线铝层(Θ2)经气隙(Θ3)传递至冰层(Θ4)，冰层(Θ4)自内表面开始融化，融冰水经冰层空隙流失，在导线和冰层之间形成气隙(Θ3)。

短路融冰时间一般较短(0.5～3 h)，电流焦耳热效应远大于阳光照射，可以忽略阳光照射的影响。融冰过程中，电流产生的焦耳热消耗于:①冰层外表面因对流和辐射产生的热损失;②冰融化需要吸收的潜热;③加热导线、冰层和空气间隙。

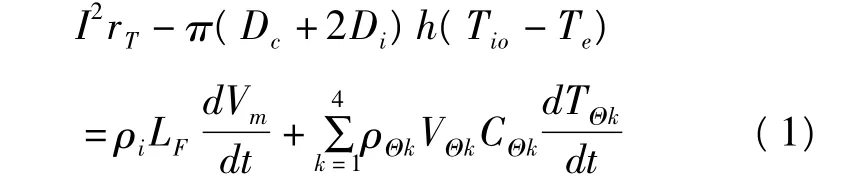
式中，rT为导线电阻率，Ω/m;Ri为冰层外表面圆半径，m;h为冰层外表面与环境热交换系数(包括对流传热和辐射散热)［6］，W/(m2·K);Vm为冰融化的载面积(单位长体积)，m;VΘk表示区域Θk的截面面积(或单位长体积)，m2;ρΘk表示区域 Θk的密度，kg/m3;CΘk表示区域 Θk的比热容，J/(kg·℃);TΘk表示区域Θk的温度，℃;Tio为冰层外表面温度，℃。

在融冰过程中，TΘk(k=1，2，3，4)是不断变化的，为时间和空间的函数，即 TΘk=TΘk(x，y，t)。根据式(1)，融冰时间的计算模型可以表示为

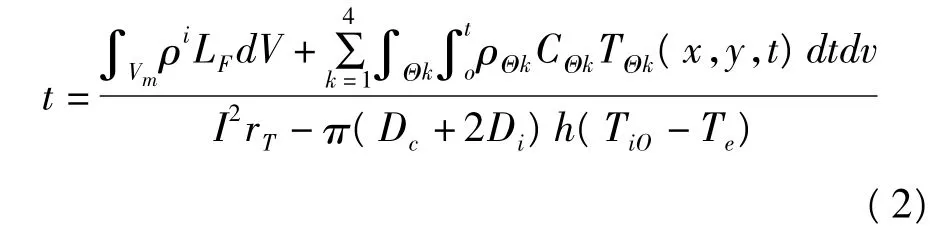
对于式(2)，如果假设融冰的体积Vm已知，且忽略导线、气隙、冰层因升温吸收的热量，即(x，y，t)dtdv=0，则式(2)便为静态融冰模型。所以，由式(2)可知，静态模型是动态模型的简化。由于温度分布函数TΘj(x，y，t)随着融冰过程中冰层的向下位移、气隙厚度等状态参量的变化而变化，使得融冰动态模型很难像静态模型那样求得解析解。

1.2 融冰时间的计算

在融冰过程中，导线融冰的动态传热方程为［3］

式中，λ为覆冰导线热传导率，W/(m·℃);ρ为密度kg/m3;Cp为比热容，J/(kg·℃)。

采用加权余量法对式(3)进行变分［6］得

式中，Wl为对应节点 l(l=1，2，…n)的权函数，取三角形单位的线性形函数;-λ∂T/∂n表示法线方向上的热流密度，W/m2。对式(4)积分，同时代入Galerkin 差分格式得［6］

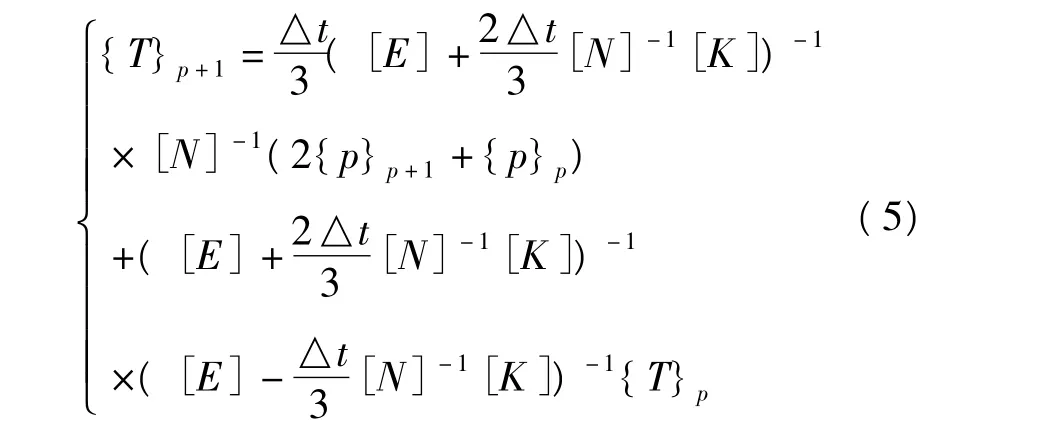
式中，［E］为单位矩阵，n×n;［K］为温度系数矩阵，n×n;［N］为温升系数矩阵，n×n;{P}p为常数项向量，n ×1，与热源和边界条件有关;{T}p=(T1，T2，…，Tn)为p时刻节点温度向量，n×1。

1.3 仿真分析

根据式(5)，采用商业软件COMSOL3.4进行计算，可得导线融冰过程中截面温度分布如图2所示。

①由图2(a)可知，当导线表面温度＜0℃时，冰层不会融化。这段时间产生的焦耳热主要用于使导线和冰层升温。②导线温度随着融冰时间的增加而增加。由于冰层的不断融化，冰层在重力作用下下移，导线两侧和下侧出现气隙。由于气隙的热阻很大，使有气隙的地方冰层融化变慢。导线上侧和冰层接触紧密，所以，导线上侧的融冰速度不会变慢。所以，气隙-冰层(Gap-Ice)呈椭圆形发展，直至冰层脱落时刻。

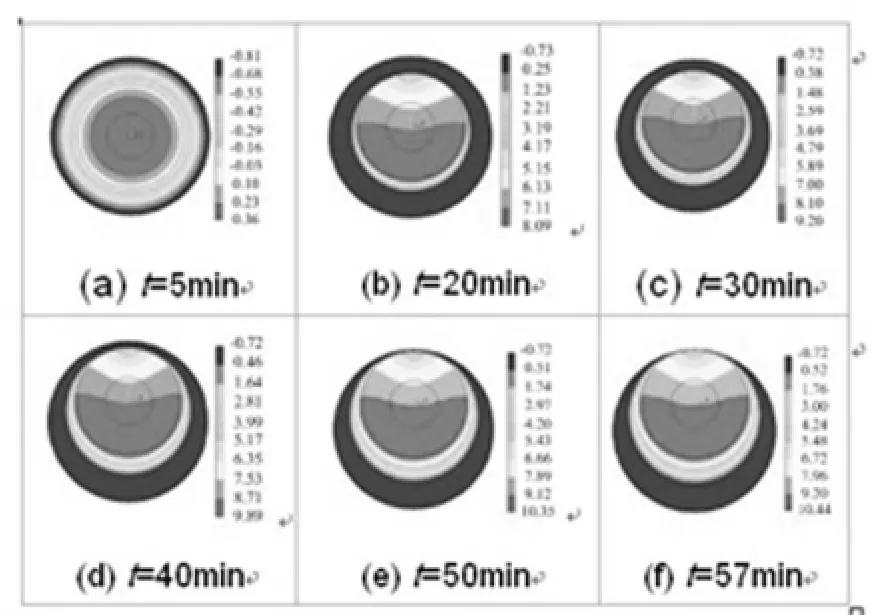
图2 融冰过程的仿真

2 试验验证

在人工气候室对以上分析计算进行了试验验证。按照图2的融冰条件，在人工气候室中进行融冰试验，得到如图3所示的融冰过程。图4则绘出了气隙增长的计算值和试验值的比较。

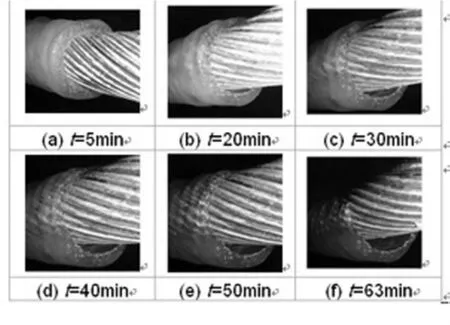
图3 覆冰导线融冰过程中

(1)图3的试验结果和图2的仿真结果基本相符。

(2)椭圆形气隙短轴和长轴的增长的试验值与仿真结果基本一致。由图4可知，随着融冰时间的增加，椭圆形气隙短轴a的增加逐步趋于饱和，增长速度随着融冰时间的增加逐步变慢，而长轴b的增速随着融冰时间的增加反而有增大的趋势。

3 结论

(1)导线融冰过程中，随着冰层的融化，冰和导线之间将形成逐步增大的椭圆形气隙，气隙的高热阻使融冰过程中导线表面温度高于0℃。

(2)在风速、环境温度以及冰厚一定时，导线融冰时间由电流密度决定。融冰电流密度必须大于临界融冰电流密度，冰层才会融化。融冰电流密度越大，融冰时间越小。

(3)电流密度、冰厚和环境温度一定时，风速对融冰时间有明显的影响，风速越大，融冰时间越长。当风速大于临界风速时，冰层将不会融化。不同电流密度所对应的临界风速不同，电流密度越大，临界风速也越大。

(4)电流密度、冰厚和风速一定时，环境温度对融冰时间有明显的影响，环境温度越低，融冰时间越长。当环境温度低于临界环境温度时，冰层将不会融化。不同的电流密度对应的临界环境温度不同，电流密度越大，临界环境温度越低。

(5)导线上覆冰的厚度越厚，融冰时间越长。

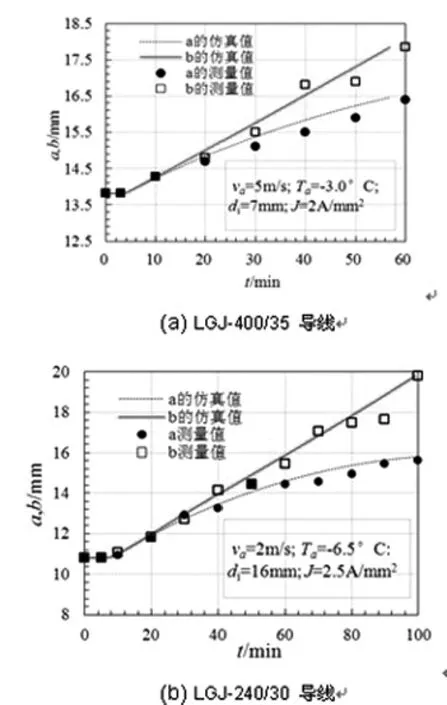
图4 空气间隙增长过程

［1］刘和云.架空导线覆冰与脱冰机理研究［D］.武汉:华中科技大学，2001.

［2］Z.P'TER.Modeling and Simulation of the Ice Melting Process on aCurrent-Carrying Conductor［D］.Universitédu Québec，2006.

［3］S.Y.Sadov，P.N.Shivakumar，D.Firsov，S.H.Lui，R.Thulasiram.Mathematical Model of Ice Melting on Transmission Lines［J］.J Math Model Algor，2007，6(1):273-286.

［4］M.Huneault，C.Langheit，R.S.Arnaud，J.Benny，J.Audet，J.C.Richard.A Dynamic programming Methodology to Develop De-icing Strategies during Ice Storms by Channeling Load Currents in Transmission Networks［J］.IEEE Transactions on Power Delivery，2005，20(2):1604-1610.

［5］M.Huneault，C.Langheit，J.Caron.Combined Models for Glaze Ice Accretion and De-icing of Current-carrying Electrical Conductors［J］.IEEE Transactions on Power Delivery，2005，20(2):1611-1616.

［6］秦妍，李维仲.利用移动网格技术模拟冰融化过程中的传热问题［J］.热科学与技术，2005，4(3):213-218.

［7］J.V.C.Vargas，A.Bejan，A.Dobrovicescu.The Melting of an Ice Shell on a Heated Horizontal Cylinder［J］.Transactions of the ASME.Journal of Heat Transfer，1994，116(3):702-708.