新疆白杨河西岸地下水水源地扩大开采可能性论证

郭 琳，郭 健，吴 彬，郭西万

(1.新疆水电设计研究院地质勘察研究所，新疆 乌鲁木齐 830052;2.新疆昌吉学院，新疆 乌鲁木齐 830052;3.新疆农业大学，新疆 乌鲁木齐 830052)

新疆白杨河西岸地下水水源地扩大开采可能性论证

郭 琳1，郭 健2，吴 彬3，郭西万3

(1.新疆水电设计研究院地质勘察研究所，新疆 乌鲁木齐 830052;2.新疆昌吉学院，新疆 乌鲁木齐 830052;3.新疆农业大学，新疆 乌鲁木齐 830052)

根据白杨河西岸地下水水源地的开采量及动态资料，分析水源地的水文地质特征，利用数理统计理论与方法，建立多元线性回归与非线性回归方程，通过拟合精度检验，证明非线性回归方程最适宜该水源地扩大开采的地下水资源预报。根据开采的变化过程，1983年实际开采量接近稳定开采阶段的平均水平，则把1983年开采量1 391×104m3确定为正常开采条件下的地下水开采量;把地下水位降低到承压含水层顶板时，极限的地下水开采量为1 856×104m，为水源地应急供水提供定量依据。

水源地;水资源;开采动态;回归分析

众所周知，地下水资源的形成是一个受多种因素，即气象水文、地质构造、岩性结构等综合因素影响的结果，很难用确定性模型来准确地表达它们之间的关系。在实际运用确定性模型的求解过程中，在很多情况下往往是人为地把某些因素加以削减或简化，这就造成在运用确定性模型来评价地下水资源时，会出现一定的局限性，甚至评价有些失真。如果能利用多年系列的地下水开采动态资料，就可以运用数理统计的原理，建立起地下水开采量与其它影响因素之间的随机模型，然后利用外推法进行地下水资源预报。

1 水源地水文地质基本特征

白杨河西岸地区埋藏分布着一个中新生界自流斜地，主要是第三系孔隙裂隙水。经过前人多次的地质及水文地质勘察，以及水源地近五十年来开发利用实践，基本证实了区内第三系孔隙裂隙水是比较丰富的。第三系沉积层在地貌上是一个由西北向东南展布的冲洪积扇;在构造上表现为由西北向东南倾斜的单斜构造。第三系沉积层是由白杨河及其支流搬运堆积而成的、是典型的河流沉积层，由砂岩、砾岩和泥岩组成。沉积厚度在北部地区10～40 m，中部地区40～60 m，南部地区50～70 m。

白杨河地区分布着一条东西向的大断裂，它切穿了中新生界，使河水沿着断裂破碎带渗漏补给粗颗粒地层中，形成水源地主要开采的含水层。

根据抽水试验资料，北部地区单井出水量一般在620～1 216 m3/d;中部地区在750～1 000 m3/d;南部地区在160～900 m3/d。矿化度由北部的 0.2～0.4 g/L过渡到南部地区的 0.5～1 g/L，水化学类型主要为HCO3—Ca·Na型水。

2 回归方程的确定

本次试图利用水源地多年的开采动态资料，主要包括历年水位和开采量监测资料，来建立一个不同区域降深和开采量之间的多元回归方程。根据该方程分析人为设置不同降深条件下的开采量变化情况，进而论证其扩大开采量的可能性。本次回归分析采用各观测井的逐年降深(取1964年初水位为初始水位)以及对应的年开量见表1。

根据表1的各区域典型观测井水位降深与对应时段的地下水开采量，本次采用SPSS statistics 17.0软件的多元回归分析功能，对1966年～1983年共17年的井区北部平均降深S1、井区中部平均降深S2、井区南部平均降深S3与水源地开采量Q的相关性进行分析，具体分析结果如下所示:

表1 各观测井逐年水位降深过程及对应年开采量

2.1 多元线性回归分析

2.1.1 多元线性回归方程的建立

在SPSS平台下，对S1、S2、S3与开采量Q采用多元线性回归方法进行分析，多元线性回归方差分析见表2，回归方程系数结果见表3。

表2 多元线性回归方差分析结果

表3 多元线性回归方程系数结果

由表3可知，采用多元线性回归分析，水源地北部、中部、南部降深S1、S2、S2与开采量Q的回归方程如下所示:

2.1.2 多元线性回归拟合结果分析

为进一步评价线性回归方程与开采量的拟合程度，将1966年～1983年共17年典型观测孔实测降深S1、S2、S3带入回归方程，计算拟合开采量，并与实测开采量进行误差分析，结果如表4。

表4 1966年～1983年实测开采量与拟合开采量对比

如表4所示，根据多元线性回归方程计算的拟合开采量与实测开采量，最大误差19.85%，最小误差0.27%。其中误差大于10%的年份占总年份的比例为29.4%，误差大于5%的年份占总年份的比例为58.8%，对开采量的拟合结果欠佳。

2.2 非线性多元回归分析

2.2.1 多元回归方程的建立

地下水开采量与不同区域的水位降深之间往往是非线性关系，要对其进行回归性分析，首先要对Q与S1、S2、S3进行线性化处理，并获取关于InS1、InS2、InS3与InQ的线性回归方程如(1)。

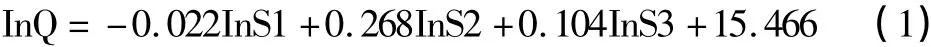
2.2.2 非线性多元回归方程拟合结果分析

按前述拟合结果分析方法，将1966年～1983年共17年的典型观测孔实测降深S1、S2、S3带入式(1)，计算拟合开采量，并与实测开采量进行误差分析，结果如表5所示。

表5 1966年～1983年实测开采量与拟合开采量对比

如表5所示，根据非线性多元回归方程计算的拟合开采量与实测开采量，最大误差13.38%，最小误差0.16%。其中误差大于10%的年份占总年份的比例为11.7%，误差大于5%的年份占总年份的比例为35.3%，对开采量的拟合结果明显优于多元线性回方程，非线性多元回归方程的方差上也同样优于线性回归方程，因此可以认为非线性多元回归方程能够较好的代表水源地开采量与各区域平均降深的关系，可以用来分析不同降深条件下的开采量，以进一步论证水源地的最大可能开采量。

3 水源地最大可能开采量论证

根据上节所建立的水源地开采量Q和水源地北部、中部、南部水位降深S1、S2、S3的非线性回归方程，按照不同的开采要求设置各区域不同的降深，即可预测各降深对应的水源地可开采量，具体如下所示:

3.1 不同开采条件下的预测开采量

3.1.1 水源地正常运行条件下的预测开采量

根据水源地建成至今逐年的地下水开采量监测数资料知，1975～2002年为稳定开采阶段，水源地开采量在1 300×104m3至1 700×104m3之间波动，在有水位观测数据期间，1983年的实际开采量与稳定开采阶段的平均值较为接近，因此可取1983年为正常运行条件下的水平年，查得该年各典型观测井水位降深S1、S2、S3，代入回归方程，即可求出水源地正常运行条件下的预测开采量，具体结果如表6所示:

表6 正常运行条件下各典型水位观测井降深及预测开采量

由上表可知，正常运行条件下水源地年最大开采量为1 391 ×104m3。

3.1.2 水源地极限开采条件下的预测开采量

正常运行条件下井内水位应高于第三系含水层的顶板，若要使水源地在持续运行条件下最大限度的开采地下水，要求运行水位维持在水源地第三系承压含水层顶板之上而不能进入该含水层，则与之对应的水源地中部与南部降深S2、S3可由典型水位观测井处的初始水位和第三系承压含水层顶板之差获得，对于井区北部地下水补给区域，其第三系含水层和第四系的松散堆积层大多直接接触，其间缺少连续的隔水泥岩，该区域地下水主要赋存在第三系和第四系中的潜水和微承压水，在1964年的初始水位已经低于了第三系含水层顶部，因此该处水位在本方案中设定为维持水源地正常运行条件下的水位，其降深S1可取表6的计算结果。综合S1、S2、S3并代入回归方程，即可求出水源地极限运行条件下的预测开采量，各典型井含水层分布见表7，具体结果如表8所示。

表7 水源地各区典型地下水位观测井含水层分布 m

表8 极限开采条件下各典型水位观测井降深及预测开采量 m

由表8可知，极限开采条件下的水源地年最大开采量为1 856×104m3。

4 结语

(1)根据对所建线性回归与非线性回归方程精度检验，提出非线性回归方程最适宜本水源地的地下水资源预报。

(2)根据开采过程的变化，选择比较稳定的开采段的开采量做为该水源地地下水资源预报的基础，为此提出了水源地有断层水和承压水补给保证，且能持续利用的地下水量为1 391×104m3，为保障应急供水的地下水极限开采量为1 856×104m3。

［1］虎肚·吐乌尔白地下水利用.中国水利水电出版社，2008.10.

［2］盛骤.概率论与数理统计.高等教育出版社，2010.

A Study on the Possibility of Groundwater Exploitation in West Bank of Baiyang River

Guo Lin1，Guo Jian2，Wu Bin3，Guo Xiwan3
(1.Xinjiang Institute of Hydropower Research and Geological Survey，Urumchi 830052，Xinjiang;2.Changji College ，U-rumchi 830052;3.Xinjiang Agricultural University，Urumchi 830052，Xinjiang)

By analyzing the production performance and hydrological characteristics of groundwater in west bank of Baiyang river，the paper builds a multiple linear regression equation and a multiple nonlinear regression equation to demonstrate the relationship between groundwater resource exploitation and hydrological characteristics.The later fitting precision test suggests that the multiple nonlinear regression equation is the best way to calculate the rational exploiting value.The exploitation data show that，the average exploiting value in 1983，which is 1 391 ×104m3，is most approximate to the exploiting value in steady exploitation stage.Therefore，the average exploiting value in 1983 is designated as the exploiting value under normal working condition.Moreover，when the groundwater level is just above the confined aquifer，the maximum exploiting value is 1 856×104m.

Water resource，water source，production performance and regression analysis

TV211.1+2

A

1004－1184(2013)05－0049－04

2013-05-07

郭琳(1971-)，女，新疆乌鲁木齐人，工程师，主要从事水文地质及工程地质勘察试验工作。