列车通过隧道时流场的二维数值模拟分析
2013-09-05王国志刘桓龙
陈 荣,王国志,邓 斌,刘桓龙
(西南交通大学机械工程学院,四川成都 610031)
列车在隧道中运行时,由于列车壁面、隧道壁面和地面对空气的阻碍,隧道内空气压力剧烈波动,引起强烈的气流变化[1]。如隧道内压力波动传入车内,会造成乘客耳鸣、耳膜疼痛等不适。列车在隧道中高速运行时,行车阻力增大,同时隧道内接触网系统受到影响。本文通过数值模拟的方法研究列车在不同的速度下在隧道中运行时流场的变化,对产生的活塞风[2-3]、隧道内的压力波动以及列车受到的空气阻力进行分析。
1 数值模拟
1.1 模型建立
列车通过隧道时引起的空气流动是三维可压缩非定常的紊流流动,由于隧道和列车都是长宽比很大的细长物体,一般将其简化成一维流动,但这种方法不能反映同一截面上不同位置处速度和压力的变化规律[4]。本文利用流体分析软件Star-cd的动网格技术,基于非稳态不可压缩流体质量守恒方程,选取K-E/High雷诺数湍流模型,采用一阶迎风离散格式,建立活塞风的二维黏性、不可压缩、不等熵非定常的紊流模型[5]。
1.2 网格的划分
由于隧道和列车实际几何形状比较复杂,为方便计算将其简化,采用常用的YZ25G型列车作为计算模型。考虑到计算成本,列车模型取5节编组,总长为126 m,高4.4 m,车头为钝形;隧道长900m,高7.2 m。模型计算区域划分见图1。图1中区域1和区域2为包括远场边界在内的大部分区域,区域3为靠近隧道壁区域,区域4随列车一起滑动。区域5为列车周围的较小区域,由于流场计算的复杂性,该区域网格必须细化。区域4中离列车较近的地方,网格需划分得较密,其它离列车较远的区域对结果影响不大,网格划分得较稀。

图1 列车过隧道计算域划分示意(单位:m)
1.3 边界条件的设定
采用Star-CD的动网格技术模拟列车通过隧道的流场[6]。图1中区域1、区域2和隧道出入口采用pressure边界,压力为标准大气压。区域3和区域4之间采用attach边界,模拟动网格的移动。列车上下采用wall边界,速度取列车运行速度值。模型前面和后面采用 symmetry边界,其它边界采用缺省的 wall边界。
1.4 动网格的建立
本文主要研究列车运动带来的流场随时间的变化,因此利用Star-CD建立动网格模型。图1中区域4为列车运动区域,即动网格区,与静止区域3之间通过attach边界进行交接,通过区域4左端网格的添加、右端网格的删减来实现列车的移动,具体的运动方式用用户自定义函数定义。
2 计算结果分析
列车由距离隧道入口90m处出发,模拟列车进出隧道的全过程。在其他条件不变的情况下,只改变列车的运行速度,分析隧道内活塞风和压力场的变化情况,列车速度V分别取20,25和30m/s。
2.1 活塞风分布
在不同车速下,车头、车尾到达隧道入口处时活塞风的速度分布见图2。
由图2可知:列车刚到隧道入口时,车头处前方空气扰动很大,隧道入口上方空间的大气也受到扰动。进入隧道时,列车以很大的速度将空气卷入隧道内,列车尾部活塞风出现漩涡。由于受到山墙的阻挡,隧道入口处的上方空气也出现了速度漩涡。在不同的运行速度下,列车通过隧道时产生的活塞效应的变化规律是相同的。但随着列车运行速度的增大,活塞风风速增大,引起的空气扰动范围增大。

图2 车头、车尾分别到达隧道入口处速度矢量图(单位:m/s)
通过模拟计算列车整个运行过程,提取距隧道入口200m处(测量点)的活塞风风速,得到如图3所示的曲线。由图3可知,在V=20m/s的情况下,当t=4 s时,该处的空气仍处于静止状态。当压缩波传播到该处时,平均流速逐渐增大。当t=14.5 s时(车头通过测量点时),流速突然减小。列车通过测量点的过程中,流速方向与列车运行方向相反,最小流速为-9.4 m/s。当t=20.8 s时(车尾通过测量点时),流速急剧增大;之后恢复并超过车头到达前的流速,最大值为11.9 m/s,这说明活塞风最大风速是在列车尾流中形成的。随着列车继续前进,气流一方面在惯性作用下继续流动,另一方面在摩擦力影响下逐渐减弱。

图3 不同车速距隧道入口200m处活塞风风速变化曲线
从图3还可以看出,不同车速下的活塞风在某点的变化趋势是相同的。列车运行速度越大,活塞风风速越大,列车的运行速度对活塞风有着较大的影响。
2.2 压力分布
在不同车速下,车头、车尾到达隧道入口处时的压力分布如图4所示。
由图4可知:列车刚到隧道入口时,前方空气受到压缩,车头出现最大正压。列车尾部空间形成负压,且在车尾处,负压最大。
提取列车进出隧道过程中车头的最大压强,变化规律如图5所示。可以看出,在V=20m/s的情况下,当t=4.5 s时(车头到达隧道入口),产生压缩波,压力发生突变,t=5.0 s时达到最大值2 710 Pa,随后车头最大压强又逐渐减小。当t=55.8 s时(车尾到达隧道出口),车头最大压强渐渐恢复明线上的压强值。比较图中3条曲线可知,在明线上和隧道内,列车运行速度越大,车头最大压强越大。
提取列车进出隧道过程中车尾的最小负压,变化规律如图6所示。可以看出,车尾驶入隧道入口的瞬间,车尾处产生膨胀波,出现压强突降,而当整个车身在隧道内运行时,车尾的最小压强波动较小。车速越大,车尾最小负压越小,列车运行速度对车尾最小压强的影响显著。
3 列车空气阻力
列车空气阻力由列车空气摩擦阻力和列车空气压差阻力两部分组成[7]。
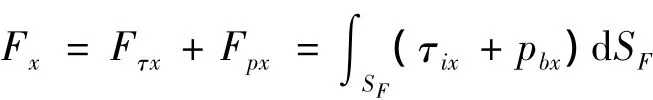
式中,Fx为列车空气阻力,N;Fτx为列车空气摩擦阻力,N;Fpx为列车空气压差阻力,N;τix为列车表面的黏性切应力在x方向的分量,Pa;pbx为列车表面压力在x方向的分量,Pa;SF为列车外表面积,m2。
由此可见,列车空气阻力与列车外形有关。在不改变其它条件的情况下,将列车头尾两端形状改为流线形[8],流线形长度为7.6 m,如图7所示,并重新建模分析。

图4 车头、车尾分别到达隧道入口处时压强云图(单位:Pa)

图5 不同速度下车头最大压强曲线

图6 不同速度下车尾最小负压曲线

图7 流线形列车(单位:m)

图8 不同外形不同速度列车所受空气阻力

表1 列车所受空气阻力
分别提取钝形和流线形列车所受的空气阻力变化曲线进行比较,如图8所示。对比可知,流线形列车所受空气阻力的变化趋势与钝形相同。两种列车所受空气阻力的具体数值如表1所示。从表1可以看出,列车外形相同时,列车运行速度越大,所受的空气阻力越大。随着速度的增大,流线形列车的空气阻力增大趋势减弱,这也说明了高速列车采用流线形的优势。在速度相同时,流线形列车所受的空气阻力约为钝形列车的0.5~0.7。
4 结论
本文利用Star-CD软件的动网格技术,模拟了列车通过隧道所产生的活塞风和压力的变化,并对不同外形的列车所受空气阻力进行了分析,结论如下:
1)列车通过隧道时的运行速度越大,产生的活塞风风速越大,相对压力越大,列车所受的空气阻力越大。在不同的运行速度下,产生的活塞效应变化趋势相同。
2)列车通过隧道内某一测点时,活塞风风速会发生突降,并达到最小值。活塞风最大风速在列车尾流中形成。
3)车头到达隧道入口时,最大压力突增,并很快达到最大值,随后逐渐减小;车尾到达隧道入口时,车尾最小压力突降;车身在隧道内时,车尾的最小压力波动较小。
4)在速度相同时,流线形列车所受的空气阻力约为钝形列车的0.5~0.7,高速列车头尾两端宜采用流线形。
[1]梅元贵,周朝晖,许建林.高速铁路隧道空气动力学[M].北京:科学出版社,2009.
[2]包海涛.地铁列车活塞风数值模拟[D].南京:南京理工大学,2005.
[3]王峰,赵耀华,胡定科.地铁隧道活塞风的简化计算[J].铁道建筑,2012(5):41-43.
[4]骆建军,高波,王英学,等.高速列车穿越隧道的二维非定常流数值模拟[J].铁道学报,2003,25(2):68-72.
[5]甘甜,王伟,赵耀华,等.地铁活塞风Fluent动网格模型的建立与验证[J].建筑科学,2011,27(8):75-80.
[6]王福军.计算流体动力学分析—CFD软件原理与应用[M].北京:清华出版社,2004.
[7]田红旗.列车空气动力学[M].北京:中国铁道出版社,2007.
[8]梁习锋,曾剑明.高速列车表面压力分布的数值计算[J].铁道车辆,1997,35(5):10-12.
