基于主成分分析法的C50高性能混凝土配合比优选研究

王起才，鲍学英，曹兴龙，张戎令

(兰州交通大学 土木工程学院，甘肃 兰州 730070)

基于主成分分析法的C50高性能混凝土配合比优选研究

王起才，鲍学英，曹兴龙，张戎令

(兰州交通大学 土木工程学院，甘肃 兰州 730070)

主成分分析法能够在保证原始数据信息损失最小的情况下，以少数的综合变量取代原有的多维变量，使数据结构大为简化。试验选取了能间接反映混凝土性能的15项主要指标，采用主成分分析法对这些间接指标进行相关的数值处理，得出了评价混凝土性能的数学模型。以兰新二线第9标段95组C50高性能混凝土样本为基础，运用该模型对C50高性能混凝土样本的性能进行了评价，并按照该样本的综合性能进行了排序，将评价结果与实际样本进行对比，结果表明，该模型的评价结果与C50高性能混凝土的实际性能符合得很好。

主成分分析法 混凝土配合比 评价模型

高性能混凝土不仅要求混凝土的拌合物具有大流动性的施工性能，而且要求混凝土具有良好的力学性能和耐久性［1］。兰新铁路第二双线第9标段施工工期为3年，线路穿越新疆戈壁地区，区段内气候环境具有干燥、大风和大温差特点［2］，这种特殊的气候环境，极易使高性能混凝土产生质量问题。研究认为能间接反映高性能混凝土性能的因素很多，这些因素对混凝土性能的影响或重或轻，如果能够确定混凝土强度及其影响因素之间的数学关系，就可以在不了解材料内部详细机理的情况下，根据数学关系探索混凝土的最优配合比，以寻求材料的最佳性能［3］。近年来，随着多元统计方法的普及与应用，主成分分析法在最大限度保留原有信息的基础上，对高维变量系统进行最佳的综合与简化，并且能够客观地确定各个指标的权数，避免了主观随意性［4］。通过对兰新二线第9标段梁体结构C50混凝土的配合比试验，利用主成分分析法，建立高性能混凝土综合评价模型，并对混凝土性能进行排序，对试验样本进行优选，为 C50混凝土最佳配合比的设计提供了一定的理论依据。

1 主成分分析法的基本原理

主成分分析法(Principal Component Analysis，PCA)是将分散在一组变量上的信息，通过恰当的数学变换，使新变量—主成分成为原变量的线性组合，并选取少数几个在变差总信息量中比例较大的主成分来分析事物的一种探索性统计分析方法［5］。其目的主要有两个:一是用有限个不可观察的潜在变量进行解释原变量的相关性，二是对变量或样本进行分类处理，用较少的指标表达大部分信息量［6］。正是利用主成分分析法的上述优点，可把高性能混凝土比较分散的性能集中到几个指标上来，从而实现对高性能混凝土配合比的优选。

1.1 主成分分析的数学模型

假定有n个样本，每个样本共有p个变量，构成一个n×p阶的数据矩阵

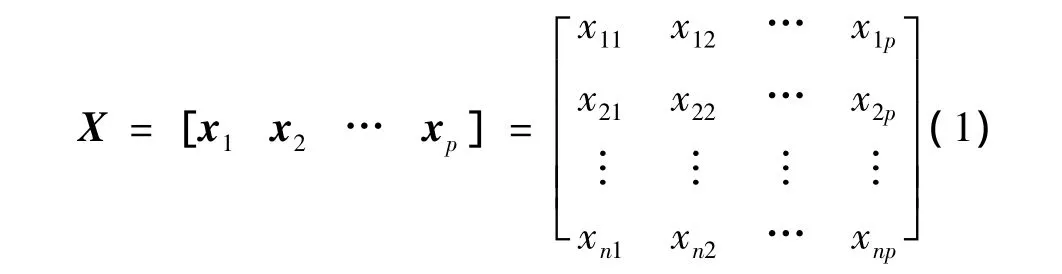
将原变量指标进行降维处理后的新变量为 F1，F2，…，Fm(m≤p)，如式(2)所示，式中，xj=［x1jx2j…x］T。

新变量F1，F2，…，Fm构成的坐标系是在原坐标系经平移和正交旋转后得到的。称F1，F2，…，Fm张成的空间为m维主超平面。在主超平面上，第1主成分F1是x1，x2，…，xp的所有线形组合中方差最大者，F2是与F1不相关的x1，x2，…，xp的所有线形组合中方差最大者;Fm是与 F1，F2，…，Fm－1都不相关 x1，x2，…，xp的所有线形组合中方差最大者。因此，新变量指标F1，F2，…，Fm分别称为原变量指标 x1，x2，…，xp的第1，第2，…，第m主成分。从以上分析可以看出，主成分分析的实质就是确定原来变量 x1，x2，…，xp在诸主成分 F1，F2，…，Fm上的载荷 lij(i=1，2，…，m;j=1，2，…，p)。

1.2 主成分分析方法计算步骤

由主成分分析的基本原理和数学模型可以看出，其估计的任务是通过确定主成分的个数，解释主成分的实际意义和它的得分，从而可以从几个或若干个备选方案里选择出较优化的方案。由于反映混凝土性能的量纲不一致，在进行主成分分析之前可对其各指标进行标准化处理，统一为无量纲的数值。

第一步:对原始数据进行标准化变换

设有n个样本，每个样本观测p项指标，得到原始数据资料，为了排除数量级和量纲不同带来的影响，用式(3)先对原始数据进行标准化处理。

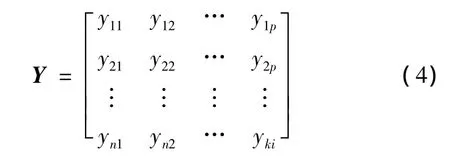
第二步:计算样本相关系数矩阵为

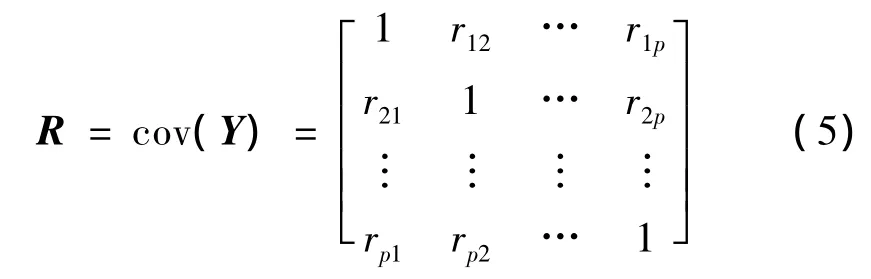
其中，rij(i，j=1，2，…，p)为原变量 yi与 yj的相关系数，rij=rji，其计算公式为

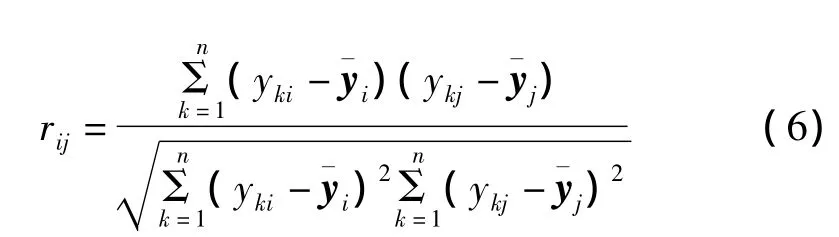
第三步:计算相关矩阵的特征值及其所对应的特征向量

由R的特征方程:|R－λE|=0，可得p个非负特征值 λi(i=1，2，．．．，p)，并将这些特征值按由大到小的顺序排列:λ1≥λ2≥…≥λp≥0。

第四步:计算主成分贡献率及累计贡献率

主成分的贡献率ηi和主成分Fi的累计贡献率 ξF，i分别如式(7)和式(8)

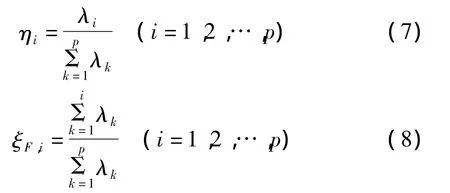
累计贡献率一般以其达到某一特定值时为准(如85%)，保留前m个主成分来确定混凝土性能。

第五步:计算主成分载荷lij

第六步:计算样本的综合得分。

由上述计算可得到样本混凝土的综合性能，即得到式(2)。可从各组比较分散的指标中找出最优化的组合。

2 利用混凝土试验样本建模型求解

首先对兰新二线第9标段C50混凝土试验样本数据进行简单的删减，保留其中能够全面反映混凝土信息指标的95组不同配合比的C50混凝土样本，部分试验数据如表1所示。

表1 C50混凝土部分试验样本

2.1 主成分分析

1)主成分分析法的适用性验证

由于试验样本各性能的量纲不同，要对其进行标准化，在得到标准化数据后利用SPSS软件对表1中的数据进行主成分分析。首先，确定一组数据是否适合做主成分分析，需要做 KMO取样适合度检验和Bartlett球形检验。KMO取样适合度检验统计量是用于比较观测变量间相关系数平方和和偏相关系数平方和指标。偏相关系数绝对值越小，说明两变量存在公共因子的可能性越大，说明可能适合做主成分分析。Bartlett球形检验是一种检验变量之间相关性程度的检验方法，它以原有变量的相关系数矩阵为出发点，检验实际相关矩阵与假设单位阵之间的差异性。如果差异性显著，则认为变量间的相关性显著，适合于做主成分分析。具体检验结果如表2所示。

表2 KMO检验

由表2中的Kaiser-Meyer-Olkin度量可知K值＞0.6，因此证明对该组C50混凝土试验样本进行主成分分析是满足要求的。Bartlett球形检验的 Sig＜0.05，说明可以做主成分分析。

2)主成分的特征值和贡献率

对C50混凝土的15项指标计算其特征值和累计贡献率，如表3所示。

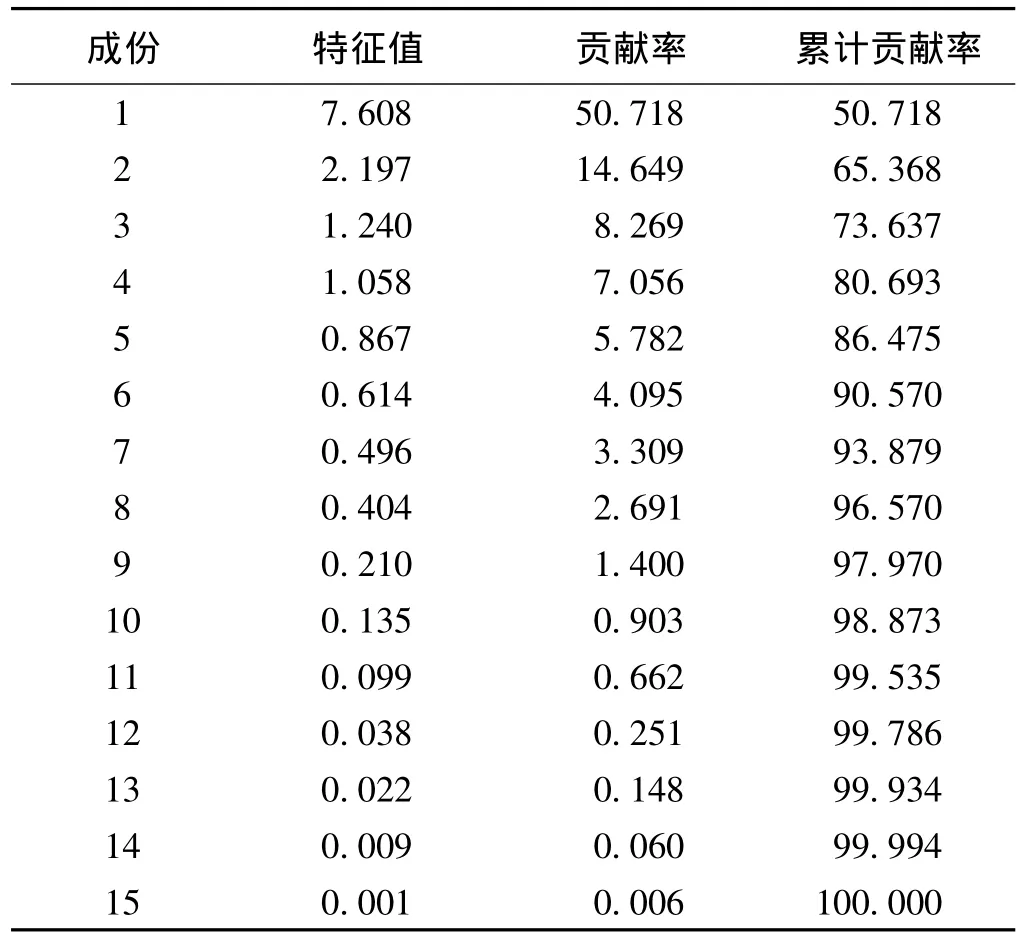
表3 特征值和累计贡献率

根据表3可知前4个成分的方差累计贡献率达80%，在15个混凝土指标中前4个指标的贡献率最大，因此，15个混凝土指标归结为4个主成分，其碎石图如图1。

由碎石图可知将15个指标化为4个主成分是成立的。同时，可以得到主成分的因子载荷图，如图2所示。由图2可以发现隶属于主成分F1的有指标3 d强度，7 d强度，28 d强度，水泥，胶凝材料;隶属于主成分F2的有粉煤灰，矿粉，细骨料，水，水胶比，56 d电通量，初始含气量;隶属于主成分F3的有粗骨料，减水剂;隶属于主成分F4的有表观密度。与专业知识基本吻合，综合来看F1代表强度，F2代表水胶比，F3代表粗骨料，F4代表密实度。

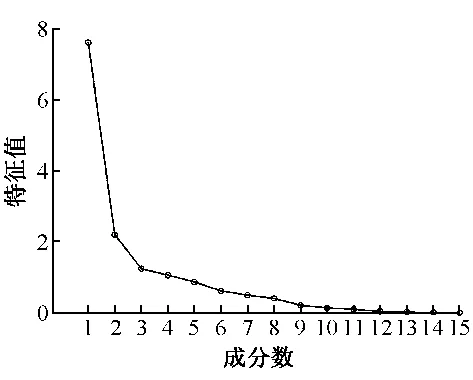
图1 指标碎石图

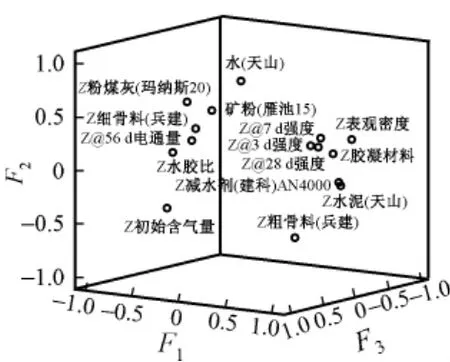
图2 主成分的因子载荷图

3)计算C50混凝土的综合性能指标

各成分的贡献率由表4可得，并以其为依据作为权重因子的权重，可得到C50混凝土各指标的综合性能指标。

表4 成分得分系数矩阵

各成分的贡献率作为权重因子的权重，可得到C50混凝土各指标的综合性能指标

根据所筛选出的反映C50高性能混凝土综合性能的4个主成分，可以计算出主成分 F1，F2，F3，F4的权重，如表5所示，根据所测试的15项指标得出C50混凝土性能综合评价表达式为

表5 各主成分综合权重

2.2 C50混凝土综合评价结果

利用MATLAB工具，计算得到了每一个样本的综合评价结果，前10名排序结果如表6所示。由表可知样本7的综合质量是最优的，因此，可以考虑采用该样本的配比为最佳配合比。

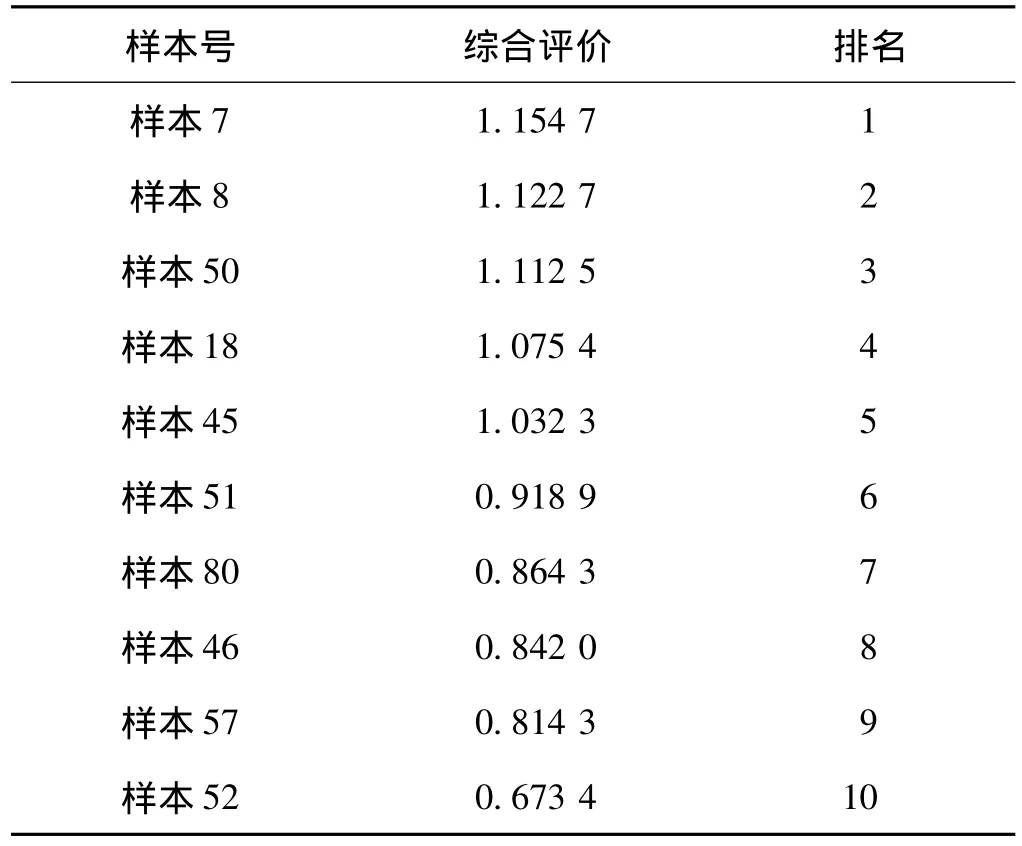
表6 前10名混凝土样本评价结果

3 结论

主成分分析法可把变量间的相关性消除，且根据降维的思想降低计算的工作量，把很多不同的变量集中到一个或几个指标上来，这样就大大减少分析数据的工作量。综合评价所得的权数是伴随数学变换自动生成的，对指标的综合评价具有一定的客观性，可在一定程度上反映出各组分性能的高低［7-9］。论文在对兰新二线第9标段C50高性能混凝土95组试验样本利用主成分分析法进行评价后得到以下结论:①运用主成分分析法可把混凝土的性能指标之间的不同量纲统一转化为无量纲的指标，通过对无量纲指标的分析可有效地比较不同组别的各性能的高低，为综合指标性能的分析提供一种快捷的方法。②综合应用各种现代优化算法，并合理选取学习样本，能够对混凝土的配合比进行定量的优化设计，从而大大减少试验量，在降低材料研制成本、缩短试验周期等方面，具有不可低估的应用价值。

［1］朱文华．浅谈铁路高性能混凝土配合比设计体会［J］．混凝土，2011(8):113-117．

［2］杨得山，王起才．兰新二线高性能混凝土桥墩抗裂性试验研究［J］．工程建设与设计，2011(7):152-157．

［3］安宁．高性能混凝土配方优化方法的研究［J］．混凝土，2006(9):72-76．

［4］潘怀兵．基于主成分分析法的沥青路面使用性能评价［J］．重庆交通大学学报，2010(12):888-892．

［5］余锦华，杨维权．多元统计分析与应用［M］．广州:中山大学出版社，2005．

［6］汪海东，曾志兴．基于主成分分析法的高性能再生混凝土性能优化设计［J］．混凝土，2011(4):51-55．

［7］张纯禹，李启令．粉煤灰混凝土强度的优化设计［J］．郑州大学学报，2002(4):88-92．

［8］齐红军．铁路客运专线高性能混凝土配合比设计优化［J］．铁道建筑，2012(7):134-136．

［9］朱星宇，陈勇强．SPSS多元统计分析方法及应用［M］．北京:清华大学出版社，2011．

U422．5;U448．21+3

A

10．3969/j．issn．1003-1995．2013．04．47

1003-1995(2013)04-0152-04

2012-12-20;

2013-01-20

长江学者和创新团队发展计划项目(IRT1139)

王起才(1962— )，男，河北晋州人，教授，博士。

(责任审编 王 红)