考虑监测噪声的陀螺仪剩余寿命在线预测

冯 磊， 王宏力， 韩晓霞， 周志杰

0 引 言

陀螺仪是惯性导航系统的敏感部件，其性能的优劣直接决定整个系统的导航精度［1］。随着使用时间的增长，陀螺仪性能不可避免地发生退化。在这种情况下，及时有效地预测陀螺仪的剩余寿命，适时采取必要的维护手段，对于提高整个惯性导航系统的可靠性与安全性有着至关重要的作用［2］。

现有的预测方法中，一般假设设备的性能退化变量直接可观测，并且可以完整地反映设备的退化状态。通过建模设备的退化过程，预测退化状态达到给定失效阈值的时间，进而预测设备的剩余寿命［3］。但是，工程实际中，直接测量的退化变量因受到各种噪声与误差的影响，不能精确反映设备的退化状态，这种测量被称为不完整测量［4］。例如，在测试惯性导航系统的陀螺仪漂移系数过程中，由于受到各种因素的影响，测量结果不可避免地存在噪声干扰与误差。为解决直接监测量带噪声的问题，可以采用状态空间模型，建模设备实际的退化过程以及退化过程与不完整测量之间的关系，通过滤波技术预测设备的剩余寿命。此外，根据滤波算法的预测方程与更新方程可以方便地实现在线预测。因此，基于状态空间模型的剩余寿命预测方法日益受到研究人员的重视。但是，现有研究中大都直接利用退化状态的估计均值作为设备实际的退化状态值，不能精确反映状态估计的不确定性对后续剩余寿命预测的影响［5-7］。

基于上述分析，文中考虑直接监测量含有噪声的剩余寿命预测问题，利用基于线性漂移的布朗运动建模陀螺仪退化过程，然后构建状态空间模型表征不完整测量与实际退化状态的关系。在利用期望最大化算法与卡尔曼滤波联合估计与更新未知参数与退化状态后，充分考虑状态估计的不确定性，将估计的退化状态分布引入剩余寿命预测过程中，得到剩余寿命概率密度函数的参数化解析形式。一旦新的监测值可用，即可更新未知参数与退化状态。相应地，可以更新剩余寿命的分布，最终实现在线剩余寿命预测。实验结果表明了所提方法具有较小的预测不确定性。

1 基于状态空间技术的剩余寿命预测

1.1 退化过程建模

假设设备实际的退化过程｛X（t），t≥0｝可由基于线性漂移的布朗运动建模，即X（t）可表示为

基于线性漂移的布朗运动被广泛用于退化过程建模，其最大优点是可以根据首达时间（First Hitting Time，FHT）的概念定义设备的寿命，进而得到寿命分布的解析形式，即逆高斯分布［8］。因此，时刻ti设备的剩余寿命可以定义为退化过程｛X（t），t≥ti｝达到预先设定的失效阈值的首达时间［9］，即剩余寿命Tr可定义为

若直接监测的退化变量不含有噪声，则可根据式（2）直接得到剩余寿命分布的概率密度函数。但是，正如上节所述，不完整测量广泛存在于工程实际中，直接监测信息不能精确反映设备的退化状态，因此，不能直接利用式（2）计算设备剩余寿命。文中利用状态空间技术解决此问题。

1.2 状态空间模型的构建

为建模直接监测与实际退化之间的关系，采用如下加性噪声模型构建观测方程:

其中，ε（t）为噪声项，假设ε（t）～N（0，σ2）且与B（t）相互独立。

为了辨识实际的退化状态，首先将动态系统（1）和（3）离散化，得到离散时间点tk＝kΔt，k＝1，2，…的状态方程和观测方程:

根据状态空间模型（4），应用卡尔曼滤波［10］估计当前时刻实际的退化状态。首先定义E（Xi｜Y1∶i）和＝Var（Xi｜Y1∶i）为利用当前时刻的整个观测序列Y1∶i＝Δ｛Y1，Y2，…，Yi｝得到的状态Xi的条件期望与方差，即Xi～N（X∧i｜i，Pi｜i）。现有研究大都直接将状态估计的均值作为其实际值，直接可以得到时刻ti，剩余寿命概率密度函数为:

式（5）没有考虑状态估计的不确定性，为了减少剩余寿命预测的不确定性，文中将估计的状态分布引入后续的剩余寿命预测中。根据全概率定律，可以得到当前时刻ti，剩余寿命概率密度函数为:

2 参数估计算法

由于模型中含有未知参数，并且状态是未知的，因此，采用EM算法解决存在未知状态时的参数极大似然估计问题。为后续表示方便，首先定义当前时刻的状态序列为Xi｝。通过迭代计算且最大化包含完整数据集（X1∶i，Y1∶i）的对数似然函数的条件期望，EM 算法能够产生一个估计序列收敛到参数的极大似然估计值［11］。令θ∧（j）表示 EM 算法第j次迭代所得的估计值，则完整数据对数似然函数的条件期望可表示为:

其中，L（X1∶i，Y1∶i｜θ）＝logp（X1∶i，Y1∶i｜θ）为完整数据对数似然函数。总结起来，参数估计程序包含如下两个步骤:

1）E 步。

计算 Q（θ，θ∧（j））。

2）M 步。

求解:

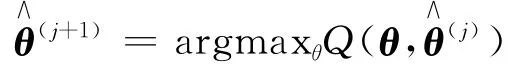
具体到文中构建的状态空间模型（4），为了计算对数似然函数的条件期望，对于k＝1，2，…，i，首先定义如下变量:

经过一系列代数运算，可以得到

其中

为降低参数空间的维数，减少计算复杂度，分别计算式（8）相对于参数λ，σB和σ的偏导数，并且令这3个偏导数为零，可得

根据一阶必要条件可知，最优的参数估计值必满足式（9）～式（11）。因此，可通过直接计算得到未知参数的估计值。

由上述推导可知，一旦获取新的观测值，就可以利用卡尔曼滤波和EM算法，估计和更新退化状态及未知参数。相应地，根据式（6）可以更新剩余寿命的概率分布，实现实时剩余寿命预测。

3 陀螺仪剩余寿命预测实验

3.1 问题描述

陀螺仪漂移是表征其性能的一项重要指标［12］。运行状态下，陀螺仪的转子高速旋转必然造成转轴的磨损，引起漂移系数的增长，当漂移系数增大到预先设定的阈值，即认为系统发生失效。本实验选取敏感轴方向的一次项漂移系数作为衡量陀螺仪退化状态的性能指标。该系数的值一旦达到失效阈值0.38°／h，即表明陀螺仪已经失效。对陀螺仪连续工作测试，采样间隔为3h，所得到的测试数据共96组，如图1所示。

图1 漂移系数测试数据

3.2 实验结果

为预测陀螺仪的剩余寿命，首先利用EM算法对参数进行估计与更新。各未知参数的估计与更新结果如图2所示。

由图2可知，随着监测数据的增加，各未知参数很快收敛到各自的稳定值，说明所提参数估计方法的有效性。其中，参数a最终的估计结果为0.004 6，σB的估计结果为0.007 8，σ的估计结果为0.004 5。

图2 参数估计与更新结果

为了验证文中方法的有效性，将文中模型与不考虑状态估计不确定性的模型做比较研究。为表示方便，将文中所构建的模型称为模型1，不考虑状态估计不确定性的模型为模型2。以第90个到96个数据为例，剩余寿命预测结果如图3所示。

图3 两种模型的剩余寿命预测结果的比较

由图3可知，两种模型的预测曲线都比较平滑，但是文中模型考虑了退化状态估计的不确定性，因此，利用文中方法预测得到的剩余寿命的概率密度曲线更加紧致，预测结果的不确定性小。由于后续的维护策略优化需要预测的剩余寿命信息，因此，文中方法可以减少维护策略建模的不确定性，降低失效风险，提高维护效率。

4 结 语

陀螺仪剩余寿命预测实践中，受各种因素的影响，直接监测的退化变量含有噪声，不能准确反映陀螺仪的退化状态。为解决此问题，构建了状态空间模型建模实际退化过程以及直接监测与退化状态间的关系，并且考虑状态估计的不确定性，将其引入剩余寿命预测过程，最终实现剩余寿命的在线预测。仿真实验表明，文中所提方法能够较好地解决陀螺仪剩余寿命预测的相关问题，并且可以减少预测的不确定性，为后续的维护策略安排提供准确而实时的预测信息。

［1］ 胡昌华，马清亮，郑建飞.导弹测试与发射控制技术［M］.北京:国防工业出版社，2010.

［2］ Zhou Z J，Hu C H，Xu D L，et al.A model for re-al-time failure prognosis based on hidden Markov model and belief rule base［J］.European Journal of Operational Research，2010，207（1）:269-283.

［3］ Si X S，Wang W，Hu C H，et al.Remaining useful life estimation:A review on the statistical data driven approaches［J］.European Journal of Operational Research，2011，213（1）:1-14.

［4］ Sun J Z，Zuo H F，Pecht M G.Advances in sequential monte carlo methods for joint state and parameter estimation applied to prognostics ［C］／／Prognostics and System Health Management Conference.Shenzhen，China:［s.n.］，2011:1-7.

［5］ Christer A H，Wang W，Sharp J M.A state space condition monitoring model for furnace erosion prediction and replacement ［J］.European Journal of Operational Research，1997，101（1）:1-14.

［6］ Carr M J，Wang W.Modeling failure modes for residual life prediction using stochastic filtering theory［J］.IEEE Transactions on Reliability，2010，59（2）:90-96.

［7］ Wang W，Carr M J，Xu W，et al.A model for residual life prediction based on Brownian motion with an adaptive drift［J］.Microelectronics Reliability，2011，51（2）:285-293.

［8］ Chhikara R S，Folks J L.The inverse gaussian distribution as a lifetime model［J］.Technometrics，1977，19（4）:461-468.

［9］ Lee M L T，Whitmore G A.Threshold regression for survival analysis:Modeling event times by a stochastic process reaching a boundary［J］.Statistical Science，2006，21（4）:501-513.

［10］ 王志贤.最优状态估计与系统辨识［M］.西安:西北工业大学出版社，2004.

［11］ Schon T B，Wills A，Ninness B.System identification of nonlinear state-space models ［J］.Automatica，2011，47（1）:39-49.

［12］ 姜楠，张双才，苏莉蔚.基于 MEMS的惯性测量系统［J］.长春工业大学学报:自然科学版，2010，31（2）:181-184.