基于灵敏度分析的载货汽车车架结构优化*
2013-09-04峰朱俊虎王
单 峰朱俊虎王 浩
(1.奇瑞汽车股份有限公司;2.合肥工业大学)
本文以某载货汽车车架为研究对象,建立优化模型对车架结构进行优化设计,通过修改灵敏部件板厚度,在保证一定的强度、刚度条件下,实现车架的轻量化[1]。
1 灵敏度分析理论
设计灵敏度是结构性能参数Tj对结构设计参数xi的偏导数(结构响应的梯度),即:
灵敏度反映其结构中各个设计变量对结构性能的影响大小[2]。在有限元线性静态优化分析过程中,约束和目标函数均有可能是通过静力平衡方程位移解得的响应[3],可表示为T=T(δ),而位移是设计变量的隐函数,用 T=T(X)表示,则:
因而,静力平衡方程可表示为:
对式(3)左右两端求关于第i项设计变量xi的偏微分,并通过移项得:
两边同乘[K]-1得:
通过式(4)可求解出位移对设计变量的灵敏度,其微分形式可表示为:
由于载荷向量F并不会随设计变量的变化而变化,即 ΔF=0,Δδ=-[K]-1Δ[K]{δ},因此有关节点位移函数的性能参数(包括目标函数或约束)对设计变量xi的灵敏度可以通过下式求出:
结构自由振动时的方程可表示为:
式中,λn和φn分别表示结构第n阶固有频率和振型;[K]表示结构刚度矩阵;[M]表示结构质量矩阵。
在有限元模态分析过程中,模态频率对设计变量的灵敏度也可以通过将式(7)左右两端对第i项设计变量求偏导数得到:
2 车架模型的建立与验证计算
2.1 模型的建立
a.模型简化。车架在建模过程中根据实际需要采取如下简化措施:略去对车架整体变形和内力分布影响很小的非承载构件[4];忽略纵横梁上的非连接孔,以更好地保证有限元网格质量;忽略半径较小的曲面倒角。
b.单元及其尺寸的选择。该车架的纵梁和横梁在建模时采用板壳单元Shell63,使用刚性连接单元RBE2、弹簧单元CELASl和梁单元CBEAM对悬架进行模拟。通过Hypermesh有限元前处理,采取自动网格划分,单个单元尺寸为10 mm,如图1所示,模型共有91045个节点,87398个网格单元。
2.2 模型的加载与约束
在所计算的满载弯曲工况和满载扭转工况中,作用在车架上的载荷除车箱加载方式是按照均匀分布载荷进行施加外,其它如发动机、驾驶室等总成的载荷采用集中施加,载荷分布形式相同,因此两种工况的加载方式相同。车架载荷分布如图2所示。
2.3 满载扭转工况下的有限元计算
通过计算分析得到,载货汽车车架大部分位置的应力都在100 MPa以下,车架等效最大应力为113 MPa,出现在第3横梁处。该载货汽车车架使用的材料屈服极限为345 MPa,则在扭转工况下其许用应力为265 MPa。因此结果表明,扭转工况下车架的等效最大应力要小于许用应力。由此可以看出,该载货汽车车架的两纵梁能够满足载货汽车强度要求。
如图3所示,满载扭转工况下车架的最大位移发生在左纵梁最前端,为60.7 mm,其中悬架位移为52.54 mm,即在满载扭转工况下车架的最大位移为8.16 mm,可保证车架在不平路面正常行驶。
满载扭转工况时出现的最大应力值较高,且该车架位移变形量也相对较大,说明该工况是较危险工况,容易使载货汽车车架的局部出现开裂或产生其他破坏。因此,在载货汽车行驶过程中,要选择相对平坦的道路,若路况较差,驾驶员应该采取措施尽量避免此危险工况的出现。
2.4 模态计算结果与试验值的比较
通过有限元软件计算与试验测量,得到该车架的前10阶模态如表1所列。由表1数据可以看出,车架的固有频率试验值和计算值非常接近,说明所建立的车架有限元模型准确。
试验共布置了67个测点,具体如图4所示。
对试验与计算得出的频率及振型进行分析,可以看出:
a.来自路面的低频激励频率一般为1~20 Hz,而该车架1阶垂向弯曲频率为29.59 Hz,避开了低频激励范围,从而避免了路面引起的车架共振。
b.车身部分固有频率为10~15 Hz,该车架1阶扭转及弯曲频率不在此范围内,从而避免了车身较大幅度的振动。
c.该车架的基频为5.91 Hz,表现为整体1阶扭转,1阶侧向弯曲频率为17.30 Hz,该车的弯曲频率较低,弯曲刚度有待加强。
d.高阶扭转与弯曲振型混杂在一起,表现为既有整体振型又有局部振型,单独或共同出现。局部模态分布呈现出前部强、中后部弱的态势。因此,建议车架后端加装一横梁,以加强尾部弯曲刚度,改善振动特性。
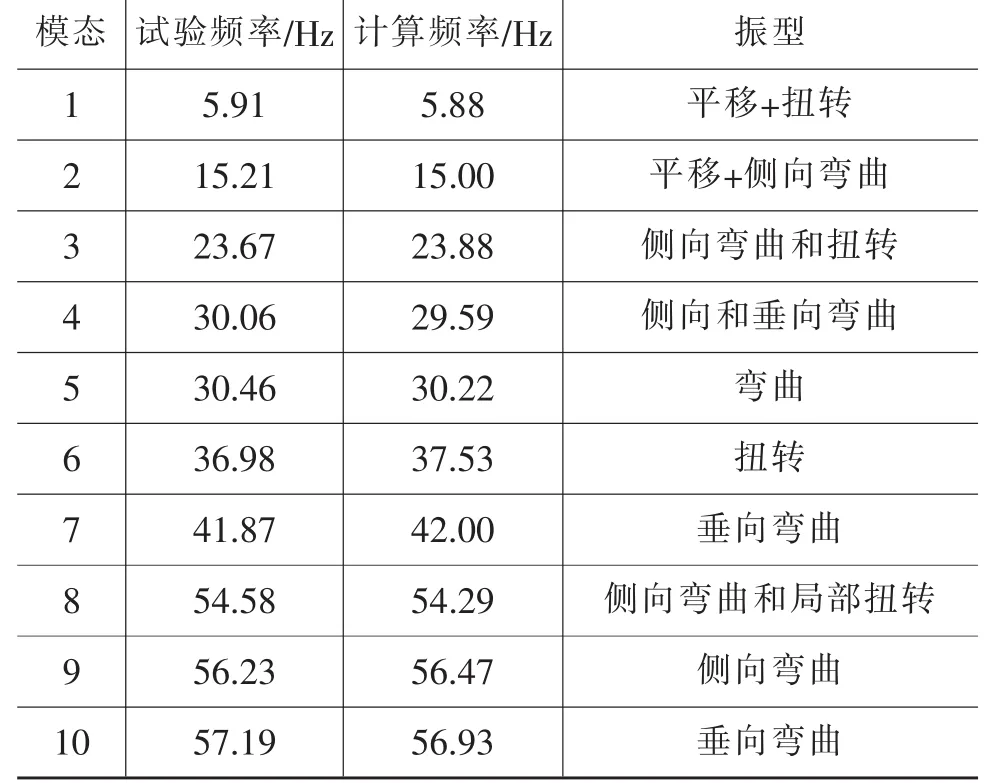
表1 试验与计算模态振型及参数
3 车架结构优化设计
3.1 灵敏度计算结果分析
对车架板件进行灵敏度分析计算,质量灵敏度用Sm表示,等效弯曲应力灵敏度用Sσ表示,Sm/Sσ为相对灵敏度。若‖Sm/Sσ‖≥1,说明随着几何尺寸厚度的变化,质量灵敏度高于或等于等效弯曲应力即刚度的灵敏度。因此,可以改变车架板件厚度,从而一定程度上减轻车架质量,在不影响其刚度的前提下实现对车架的轻量化。车架部分板件的灵敏度计算如表2所列。
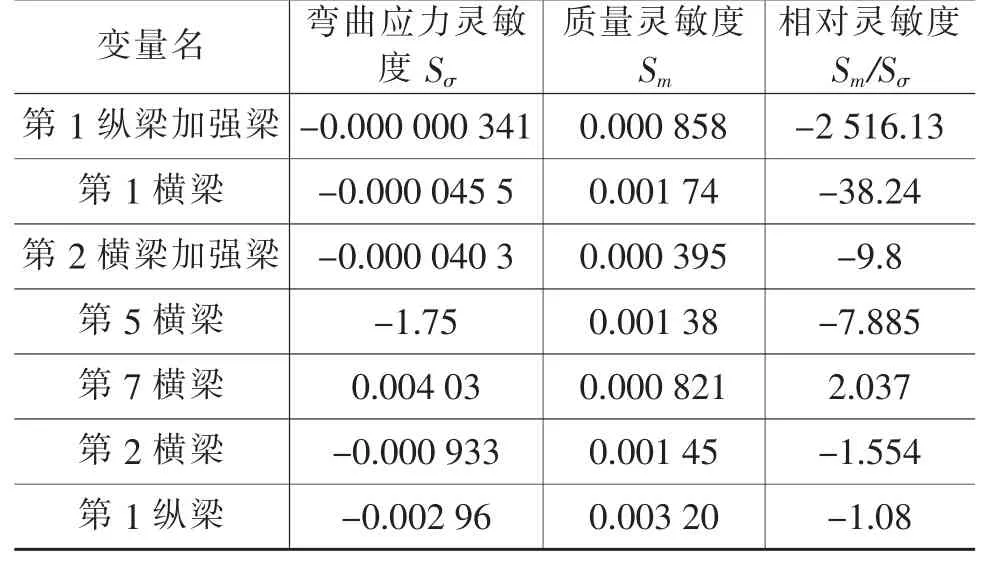
表2 车架部分板件的灵敏度计算结果
3.2 轻量化设计
a.设计变量。根据车架板件灵敏度分析结果,选出15个相对灵敏度值较大的板件为进行轻量化设计的设计变量,并使其变化小于10%。
b.状态变量。为了保证车架在满载弯曲工况下的刚度条件,选择其最大应力为状态变量。
c.目标函数。实现轻量化的目标就是减轻车架质量,因此将车架总质量设为目标函数,选择局部逼近法对目标函数进行迭代。结合车架的制造工艺,结果取两位有效数字,优化前、后迭代结果如表3所列。
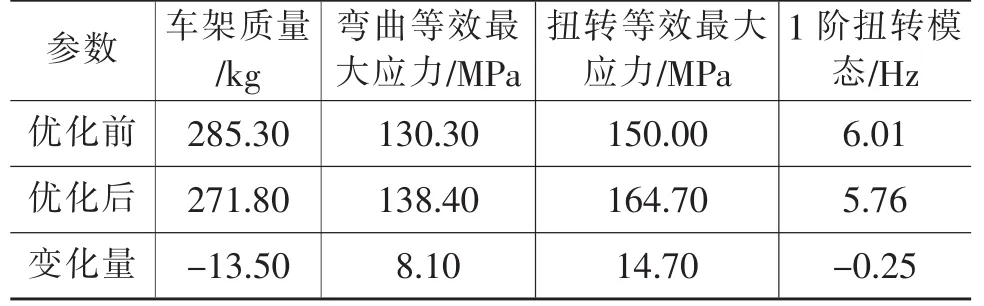
表3 迭代结果
3.3 优化结果分析
由表3可知,在满载弯曲工况下,优化后车架的最大等效应力增加8.1 MPa;满载扭转工况下,车架最大等效应力增加14.7 MPa;车架的1阶模态频率降低0.25 Hz;车架质量与原质量比较减少了13.5 kg,约减少4.7%。该车架横、纵梁材料分别为B510L和B550L,屈服极限为355 MPa和400 MPa,有较大的安全裕度,同时低阶模态频率远未达到该车发动机的怠速频率35 Hz左右,动态性能较好。表4是优化前、后板件厚度结果的比较。从表3和表4可以看出,通过降低板件厚度,能使车架质量得到合理分配,在保证车架静、动态特性的前提下,车架质量减轻效果明显,达到了轻量化目的。
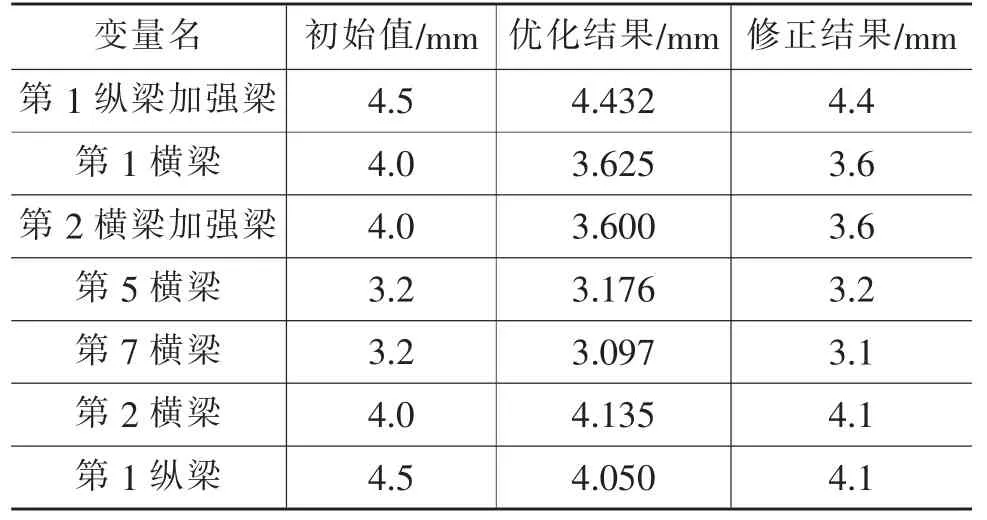
表4 优化前、后板件厚度结果的比较
1 李志祥,王军杰,吴德宏.边梁式车架的结构灵敏度分析及设计优化.机械设计与制造,2010(3):48~50.
2 马讯.基于有限元法的结构优化与灵敏度分析.机械科学与技术,2002(4):558~561.
3 梁醒培,王辉.基于有限元法的结构优化设计.北京:清华大学出版社, 2010:98~153.
4 李承德.整车系统多自由度模拟及随机振动响应分析.吉林工业大学学报,1993(3):26~41.
5 巫世晶,潜波,路红山.车辆传动系扭转振动分析系统研究与开发.系统仿真学报,2006,18(11):3100~3103.
6 曹文钢,曲令晋,白迎春.基于灵敏度分析的客车车身质量优化研究.汽车工程,2009, 31(3):278~231.
7 管琪明,尹健,等.基于神经网络和遗传算法的结构动力特性优化研究.机械科学与技术,2005(1):35~37.
8 高光波,王丽英.参数化的有限元分析技术在SX2190E型车中的工程应用.机械设计与研究,2005(4):17~22.
