燃料电池城市客车储氢瓶疲劳分析

唐学志 赵雨东 樊 彬 王文军

（清华大学 汽车安全与节能国家重点实验室）

1 前言

燃料电池城市客车作为新能源汽车的代表之一，其安全性备受关注。燃料电池客车的安全包括氢安全、电安全及碰撞安全等。在3项安全问题中，氢安全最被人们所关注。氢安全是指氢的特性引起的安全问题，主要涉及高压储氢瓶、供氢管路和燃料电池。国外关于燃料电池客车的氢安全问题的研究主要集中在氢泄漏、着火安全性等方面，而关于储氢瓶疲劳方面的研究未见相关报道；我国在这方面的研究也处于起步阶段。

本文所研究的储氢瓶是我国某企业生产的铝合金内胆碳纤维全缠绕复合瓶，瓶口通过螺纹连接安装了某公司开发的质量为6.71 kg的集成阀，集成阀和储氢瓶随车振动时可能会引起储氢瓶瓶口附近疲劳破坏，为此，通过试验测量并结合相关理论对储氢瓶瓶口附近的疲劳强度进行分析研究。

2 分析流程

根据文献[1]～文献[7]确定储氢瓶疲劳分析流程为:

a.通过试验模态分析测量装有集成阀储氢瓶的前几阶固有频率及其振型，进而找出储氢瓶的关键频率和振型；

b.测量燃料电池城市客车实际运行时车顶的振动情况，得到车顶振动的功率谱密度（PSD）和时域数据；

c.根据实测PSD谱和时域数据，简化得到振动试验台所需的评价谱 （PSD谱和正弦定频谱），将储氢瓶安装在振动台上，按照各评价谱分别激振，同时测量瓶口的动态应变；

d.根据所测动态应变计算出等效应力幅及等效平均应力，得到多轴疲劳理论下的Goodman图，分析储氢瓶的疲劳特性。

3 储氢瓶试验模态分析

3.1 主要设置

理论上试验模态分析是用力锤敲击物体得到输入信号 f（t）和物体上的加速度响应信号x（t），然后进行频谱变换得到频响函数 H（f）=X（f）/F（f），再根据模态参数估计算法得到物体的固有频率、模态阻尼及模态振型。

储氢瓶的试验模态分析方法为，利用细钢丝绳悬吊储氢瓶（图1），采用PCB公司加速度传感器和具有硬塑料锤头的力锤。传感器安装位置见图2。储氢瓶模态试验的测点为64个，瓶口模态试验的测点为39个，每个测点敲击3次，模态参数估计算法选用系统实现算法（ERA）。

3.2 试验模态分析结果

在储氢瓶装有集成阀情况下，试验模态分析得出的瓶体前3阶固有频率和第1阶振型分别如表1和图3所示。由表1和图3可看出，储氢瓶的第1阶固有频率远高于正常车顶的分析频率（0～75 Hz），且振动主要发生在储氢瓶中部。

由于储氢瓶瓶口附近的疲劳特性更关键，所以对包括集成阀在内的储氢瓶前端瓶口进行了瓶口试验模态分析，结果如表2和图4所示。由表2和图4可看出，第1阶振动的最大振幅发生在集成阀的质心附近，第1阶固有频率也远高于正常的车顶分析频率。

表1 储氢瓶前3阶固有频率 Hz

表2 瓶口前3阶固有频率 Hz

由上述试验结果可知，在正常的运行过程中，燃料电池城市客车的储氢瓶瓶体和集成阀的第1阶共振是不会发生的，储氢瓶的疲劳应主要受车顶振动的影响。

4 车顶振动测量

为能在振动试验台上重现燃料电池城市客车储氢瓶口附近振动情况，以便进行疲劳评价，对实际运行的燃料电池城市客车储氢瓶口附近的车顶随机振动进行了测量。对所测数据进行频域和时域处理后，得出了振动试验台重现实际振动所需要的PSD，以及能在振动试验台上产生比实际振动强度大的加速PSD和最大峰值正弦谱。

测试所用燃料电池城市客车作为公共汽车每天运行于北京颐和园北宫门与人民大学东门之间，行程为15 km，且每日需从颐和园北宫门返回加氢站，行程为10 km。

如图5所示，在1个储氢瓶靠近瓶口的前支架附近的车顶上布置了1个加速度传感器。共测量3组数据，第1组和第2组数据为客车在往返全程载客路线行驶时测得，第3组数据为客车返回加氢站过程中测得。储氢瓶前支架附近车顶振动测量结果（第1组数据）见图6。

由图6及其它2组数据（本文略）可知，车顶的振动主要集中在20 Hz内。考虑到振动试验台难以实现频率低于2 Hz的振动，以及功率谱密度中应尽可能反映实际振动能量所在的频率范围，所以对2～200 Hz频率范围内的功率谱密度进行分析，得到的可用于振动试验台激振并重现车顶振动的功率谱密度见图7。在2～200 Hz频率范围内，选取功率谱密度恒为6.299×10-4g2/Hz，可得到加速功率谱密度谱。

根据测量数据及最大峰值频率分析理论，可得出3组测量时域上的最大加速度值及其对应的频率，即最大峰值正弦评价谱，见表3。

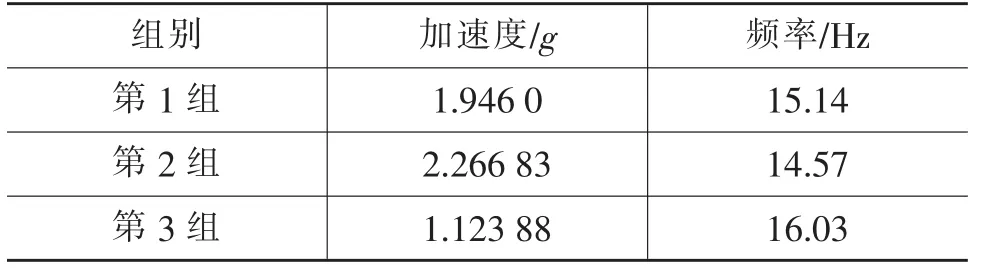
表3 最大峰值正弦评价谱

5 振动重现及动态应变测量

用上述测得的PSD、加速PSD和最大峰值正弦谱，在振动试验台上对储氢瓶激振，使储氢瓶瓶口附近重现实车运行条件下的振动情况，或产生比实际运行情况更剧烈的振动，采用应变法测量储氢瓶瓶口附近的动态应力。

因储氢瓶较长，所以在振动台上安置储氢瓶时，将激振基座支撑在储氢瓶前端靠近瓶口的位置上，而瓶的后端采用2个带轴承的小轮（简称车轮）实现铰链支撑（图8）。应变片A、B分别贴在储氢瓶瓶口的上、下端。

6 疲劳分析

基于多轴疲劳理论和Goodman疲劳准则对储氢瓶的疲劳情况进行分析。

首先根据应变片在 3 个轴（0°、45°、90°）上的应变得到主应力，然后计算出最大交变应力幅和最大平均应力，再根据多轴疲劳状态下的等效应力幅和等效平均应力计算方法[7]，计算出不同评价谱下激振瓶口振动状况的等效应力幅Sqa和等效平均应力Sqm，见表 4。

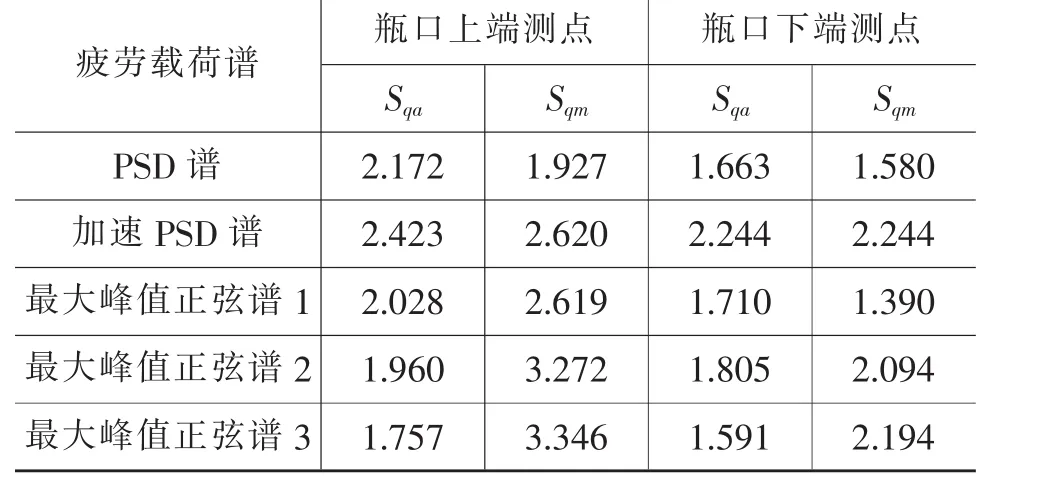
表4 各疲劳载荷谱振动下的Sqa和Sqm值 MPa

根据储氢瓶瓶口材料、结构尺寸和载荷情况以及文献 [8]，得出储氢瓶构件的等效屈服极限Sy=21.88 MPa，等效疲劳极限Sf=9.95 MPa，等效拉伸极限Su=24.88 MPa。

根据不同评价谱下激振引起储氢瓶瓶口振动的等效应力幅和等效平均应力，以及储氢瓶构件的各疲劳极限，可作出储氢瓶在各评价谱振动情况下的Goodman图。图9为功率谱密度评价谱（图7）振动下的Goodman图。

从图9及表4中其它各评价谱振动的Good⁃man图（本文略）可知，在各疲劳载荷谱下，瓶口上端测点A和下端测点B都在Goodman疲劳分析图中强度可接受的区域内，说明A、B测点及瓶口内螺纹危险点都是安全的。但A点的等效应力幅和等效平均应力都大于B点，表明A点的疲劳强度比B点略低。

加速评价PSD和最大峰值正弦谱振动下（本文略），等效应力幅和等效平均应力变化幅度都在1～4 MPa的范围内，说明储氢瓶安装集成阀后，在瓶口疲劳中起决定因素的不是实际行驶过程中由集成阀振动引起的应力变化，而可能是由储氢瓶充放气过程和充放气次数导致的。

7 结束语

为分析某燃料电池城市客车储氢瓶因悬置安装集成阀引起的瓶口附近疲劳情况，通过测量储氢瓶模态和实车运行时的车顶加速度，得出在振动试验台重现振动所需的疲劳评价谱。利用评价谱在振动试验台上重现了储氢瓶振动，测量了储氢瓶瓶口在各种评价谱下的动态应力，根据多轴疲劳理论分析了储氢瓶瓶口附近的疲劳特性。分析结果表明，储氢瓶瓶口的疲劳强度在可接受的区域内，集成阀的振动不是储氢瓶瓶口疲劳的决定因素。

1 Uday Senapati， Yogesh Dhage， Vinaya Sawant， et al.Ac⁃celerated Test Method for Validation of Vehicle Components Subjected to Fatigue Failure.SAE 2007-26-072.

2 Yi Zhang，Mohammad Usman.Life Prediction for Lighting Bulb Shield Designs Subjected to Random Vibration.SAE 1999-01-0705.

3 Steve Bogert.Integration of Fatigue Technology with Modal Analysis.SAE 933068.

4 Hong Su.Vibration Test Specification for Automotive Prod⁃ucts Based on Measured Vehicle Load Data.SAE 2006-01-0729.

5 Jack A Collins.Mechanical Design of Machine Elements and Machines.New York :John Wiley&Sons， Inc.2003.

6 H.O.福克斯，R.I.斯蒂芬斯，著，漆平生，徐桂琴，译.工程中的金属疲劳.北京:中国农业机械出版社，1983.

7 Ralph I Stephens， Ali Fatemi， Robert R Stephens et al.Metal Fatigue in Engineering （second edition）.New York:John Wiley&Sons，Inc.2000.

8 John H Bickford.An Introduction to the Design and Behav⁃ior of Bolted Joints （Second Edition）.New York:Marcel Dekker，Inc.1990.