基于子空间算法的批量生产过程配方分析

刘珊中， 郎新科

（河南科技大学 电子信息工程学院，河南 洛阳 471003）

在批量生产过程中，配方定义了产品的生产要求所需的信息。改变配方，相同的设备组合可以生产不同的产品，不同的设备也可以生产相同的产品，因此极大地增强了批量生产的灵活性，缩小了产品更新的周期［1］。所以在批量生产过程中，经常会出现配方的改变，但是对于一个生产过程来说，配方的每次改变相当于给控制过程增加了一个阶跃干扰信号，对固定参数的控制器、软测量仪表的精度带来很大的影响，从而对设备和生产过程造成影响。考虑能否根据配方的相似度对配方数据进行聚类，只针对这几类配方数据对控制参数进行调整，这样只需要设置几组参数即可，当配方变化时，相应的控制参数调整到最佳的值即可。

文献［2］使用一种改进的模糊聚类的算法对配方进行分类，文献［3］使用了概率神经网络的方法对配方进行分类，这2种办法对于简化的配方模型聚类都取得了很好的效果，但是简化的配方模型并不能体现配方数据大规模、高维的特点。对于大规模高维的配方数据这些方法能否适用，还有待考虑。

本文使用一种改进的子空间聚类算法，能够针对配方数据的特点进行聚类，并与以前的配方聚类算法以及传统的子空间聚类对比，显示该算法的优越性。

1 配方模型的建立及数据预处理

1.1 配方模型的建立

在S88标准中配方包括主配方、现场配方、一般配方和控制配方。配方的内容一般包括5个方面的信息：标题（Header）、过程（Procedure）、公式（Formula）、其他信息（Other information）、设备要求（Equipment requirements）［4］。标题包括了该配方对应的产品名称、配方制作的地点、配方制作的时间表和有效期、配方的制作人员等有关信息。过程主要是配方执行中具体的操作步骤，如添加物料的顺序等。公式包括了生产过程的输入、输出和操作参数。其他信息通常有额外的文件对配方进行阐释，虽然这些信息并不是在生产过程中必须执行的，但是也是配方发送者与接受者之间认可的，例如合同文件、产品的结构图甚至是期望的产品图片。设备要求是生产过程对设备的要求，例如生产的材料、设备的类型［3］。

为了对配方进行建模，需要对配方数据进行简化处理，由于本文所研究的配方聚类只是针对某个批量单元过程而不是针对整个批量生产过程，因此配方过程可以略去，批量生产过程的单元设备一般是不变的，因此也可以省略，其他信息与实际的批量生产过程并无联系，也可以忽略。最后简化得到配方模型由配方名、原料、加工顺序和操作参数4个要素组成，见表1所列。

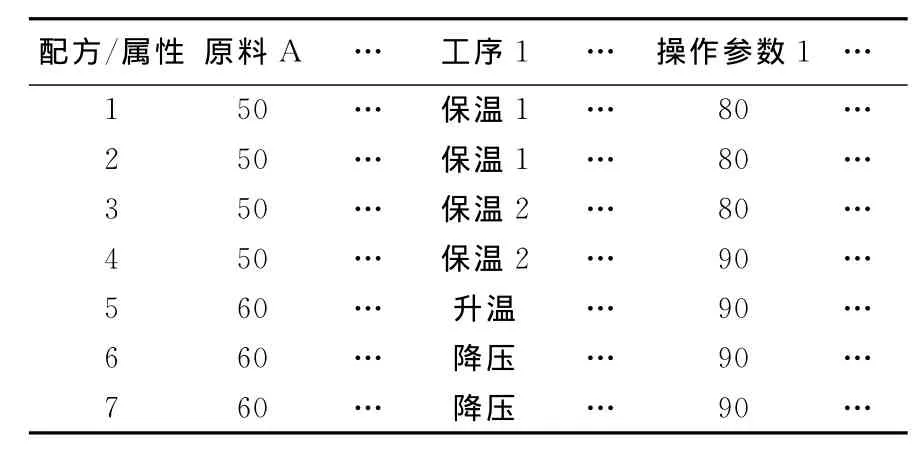
表1 配方示例数据

配方中常出现的数据类型有：区间标度型、二元型、标称型、序数型及混合型等。相似性是聚类定义的基础，对大多数聚类过程而言，对来自同一特征空间的2个样本之间的相似性度量都是必要的。由于特征的种类和范围多种多样，相似性量度必须根据具体情况谨慎选择。

1.2 基本聚类

定义1（基本聚类） 为了处理不同的数据类型，需要对不同类型的数据做前期处理，对于连续型（区间标度型）数据采用传统的k－均值聚类算法在每一维上对所有数据对象进行聚类；对于分类型数据，根据分类数据的无序性特点，在每一维上将属性相同的数据对象作为一个自然类。并把以上方法产生的每一维上的聚类称为基本聚类，记为C1。

对于表1的配方数据，采用上述方法进行基本聚类，结果见表2所列。

表2 基本聚类表

2 一种改进的子空间聚类

2.1 算法要求及算法框架

2.1.1 算法要求

配方数据是包含了多种数据类型的大规模高维数据。传统的聚类方法大多只针对数值型数据，而子空间聚类在高维数据的聚类中表现出了其自身的优势，配方数据的特点决定了一般的聚类算法很难达到配方聚类的要求［5］。

为了达到配方聚类的目的，可以借鉴传统的子空间算法和针对分类数据的聚类算法，对子空间算法进行改进，使其能够针对不同数据类型的大规模、高维数据（配方数据），可以发现任意形状和不同密度的子空间，并在此基础上提高子空间算法的可靠性。

2.1.2 算法框架

本文采用一种改进的子空间算法来对配方数据进行聚类。该算法使用一种新的聚类间相似度度量的方法，通过保留k最相似聚类确定子空间的搜索方向，并将子空间聚类扩展到不同的数据类型，以便能够进行配方聚类。其算法步骤如下：

（1）每一维上找到基本聚类，将不同类型的数据转换成相同的垂直表示方式。

（2）选择合适的k值，为每个基本聚类找到k个最相似聚类。

（3）采用合适的局部密度阀值，根据k值确定的子空间搜索方向找到可以合并的候选，通过合并候选聚类得到子空间聚类。

（4）若结果中存在未被任何子空间聚类覆盖的数据对象，则将根据其与现存子空间聚类的相似性将其分配到相应子空间聚类中。

（5）处理剩余的数据点。

2.2 相关定义

定义2（Jaccard相似度） 给定基本聚类c1，c2∈C1，其中，c1∈Ai，c2∈Aj，且i≠j，基于Jaccard系数的相似度（δ）定义为：

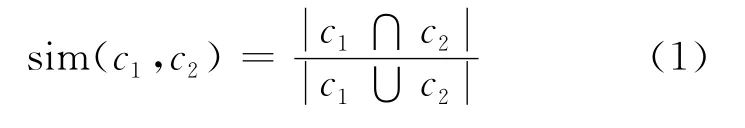
其中，A＝（A1，A2，…，Ai，…，Aj，…，Am）代表一个数据维集合；A＝A1×A2×…×Am代表一个m维的数据空间；i和j表示维；分母主要用于将数值归一化至0～1之间。

定义3（最相似聚类） 给定聚类c∈C1，c的最相似聚类 MSC（c）∈C1满足条件：∀cp∈C1，sim（c，MSC（c））≥sim（c，cp），其中，c≠MSC（c）。

定义3有助于发现大的聚类而忽略一些小的但又对配方有意义的聚类，且由于子空间聚类的特点，一个基本聚类中的数据对象可能被多个子空间聚类包含，因此进一步给出定义4。

定义4（k最相似聚类） 给定基本聚类c∈C1和正整数k，c的第k个最相似聚类称为k最相似聚类，记为MSCk（c），c的第k个最相似聚类满足：

这样定义有助于在合并初期找到相似度最大的聚类，同时又不丢失对子空间聚类贡献较大的基本聚类。通过给定的k值，能够确定子空间的搜索方向。采用合适的k值就可以覆盖整个子空间，这样既不会忽略较小的有意义的基本聚类，又可以缩减子空间搜索。

对于表2的基本聚类，取k＝2，得到c1的最相似聚类：

定义5（子空间合并候选） 给定Sn子空间和已合并到其中的n个基本聚类c1，c2，…，cn∈C1，Sn子空间的合并候选为这n个基本聚类的k个最相似聚类的交集，记为SCn。

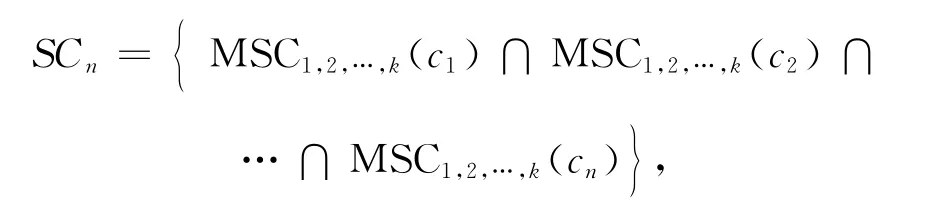
其中，c1，c2，…，cn为Sn子空间中已经合并的基本聚类。

在表2中，对于子空间S2与已合并的c1、c7，给定k＝2，得到SC2＝｛c3｝。

2.3 局部密度阀值

对于给定的子空间合并候选，需要合适的标准来选择要合并的基本聚类。在以往的子空间算法中如CLIQUE［6］中采用全局密度阀值［7］，其缺点是忽略了子空间聚类本身的特点，将其数据看作是均匀分布的，这样会使遗漏包含数据对象较少，但是对于相对密集的配方聚类，这些空间对于配方聚类的作用是不可忽略的，对于配方数据，这样的全局密度阀值显然是不可取的。所以考虑不同的子空间采用不同的局部阀值。

假设th（Sm）为Sm子空间的密度阀值，nm为Sm子空间的数据对象数目：∀⊂S，假设是密集的，如果th（）≥th（Sk），则子空间Sk⊂是密集的。

本文根据子空间的期望密度设定子空间的密度阀值如下：

其中，m为给定值，对于配方数据一般取值为0～1。

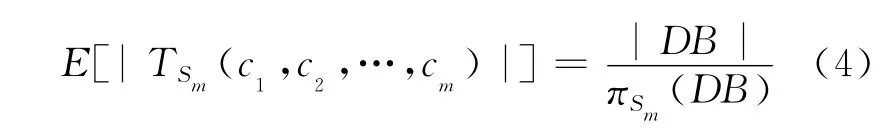
其中，DB代表由n个位于m维特征空间的数据对象组成的集合，即Xi·Aj｝，其中，点的第j个属性值为其在Aj维上的取值。

2.4 子空间合并

定义6（子空间合并聚类） 给定基本聚类cx，cx是Sm子空间的合并聚类的条件是：其中，左式为c1，c2，…，cm，cx之间的密度。

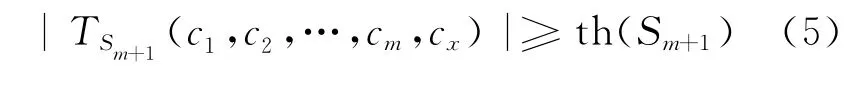
在表2中，对于子空间S2与已合并的c1、c7，给定密 度 阀 值 M＝0.85，则 th（S3）＝1.4，即c3为子空间S2与已合并的c1、c7的合并候选。

2.5 子空间搜索

如果子空间已没有可合并聚类，并且当前子空间不为结果子空间MS中任何子空间的子集，那么当前子空间加入MS中，否则继续子空间搜索。子空间搜索算法描述如下：

输入：候选子空间Sp、m、k

输出：子空间结果集

返回子空间结果集MS；

2.6 剩余点处理

在子空间搜索算法结束后，有时候会出现没有分类到子空间聚类中的数据，将其称为剩余点。计算剩余点与其相应属性的子空间聚类的相似度，对比设定密度阀值判断剩余点归为子空间聚类，还是判定为噪声点。

3 配方聚类结果与分析

（1）构建配方数据集。为了全面测试本文算法性能，在实验中使用的配方数据集为人造的数据集和真实的数据集。其中人造数据集为SQL Server产生的多维数据集，共50维，15 000个数据对象，包括6个不同维度、不同密度的子空间聚类；其中，第3个和第5个子空间聚类数据对象分布最稀疏，且不包括全维上的聚类。实验中真实数据集采用UCI［8］数据库中的多维数据集zoo、Car Evaluation、Computer Hardware。其中，zoo包含101个样本，每个样本有17个特征；Car E－valuation包含1 728个样本，每个样本有6个特征；Computer Hardware包含209个样本，每个样本有9个特征；这3个数据集都是包含了不同类型的数据值，完全可以看作配方数据。

（2）算法的可行性分析。将本文算法与CLIQUE、SUBCLU算法在人造和真实数据集上的聚类准确度作比较。通过采用取得最好聚类结果的参数，得到基于人造数据集的准确度，如图1所示。可以看出，本文算法在密度较低的第3个15维子空间和第5个25维子空间的准确度均高于CLIQUE和SUBCLU算法。传统的子空间聚类算法CLIQUE和SUBCLU不能够处理分类属性的真实数据，对比于文献［2］、文献［3］中的算法，本文算法聚类准确度高于这2种算法，更适用于处理不同类型的数据，见表3所列。

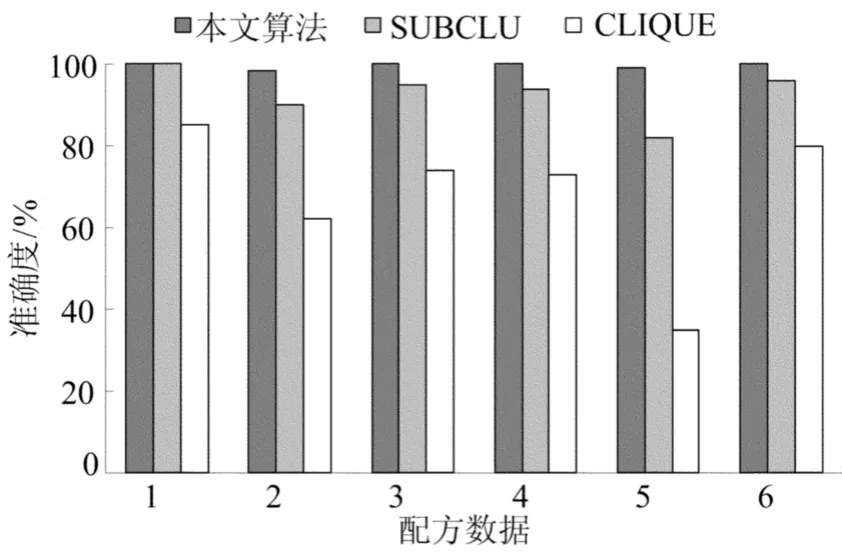
图1 基于人造配方数据集的准确度

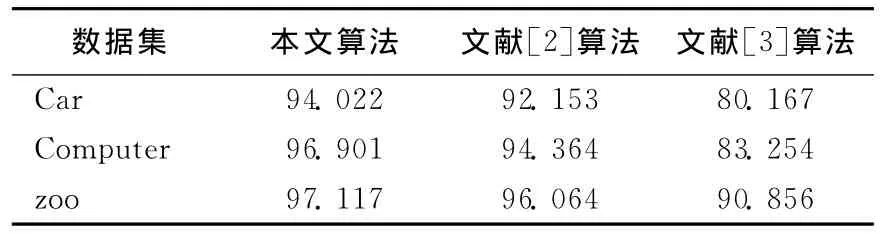
表3 基于真实数据的配方聚类准确度 %

（3）算法的伸缩性对比。对比本文算法与CLIQUE、SUBCLU［9］、文献［2］、文献［3］算法在人造数据集和真实数据集上的伸缩性，图2所示为以上5种算法对数据对象数目伸缩性的比较结果。图3比较了5种算法对数据维数的伸缩性。可以看出，文献［2］中算法在数据维数较低的情况下，具有非常好的聚类效果，但是随着维数和数据个数的增加所需的时间也呈指数增长。其他4种算法与数据维数都呈线性关系，但本文算法在数据维数的伸缩性上优于其他4种算法。

（4）参数调试。最相似聚类数k和密度阀值d2个参数的改变会对配方聚类准确度造成影响。图4给出k取不同值时对配方聚类准确度的影响，随着k值的增大，聚类准确度有所改善，对于文中的配方数据，当k值在15～20之间时，可以达到最好的聚类精度。图5反映了密度阀值对聚类准确度的影响，当d取值在0.80～0.90之间时，算法能够取得最好的聚类效果。

图2 数据对象数目的伸缩性对比

图3 数据维数的伸缩性对比

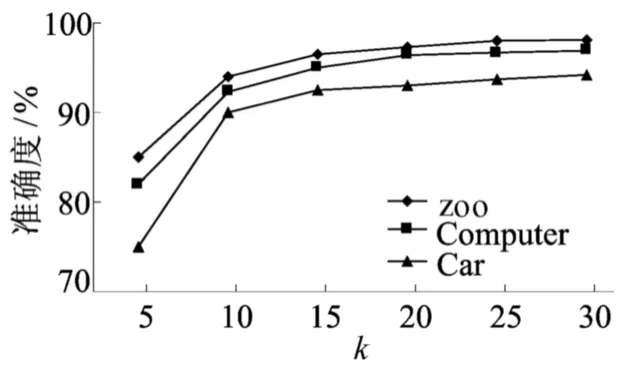
图4 参数k对聚类准确度的影响

图5 参数d对聚类准确度的影响

4 结束语

在批量生产过程中，配方聚类有助于提高批量生产过程的产品更新周期，避免产品更新时重新对配方进行处理，并且可以降低配方切换时对固定参数的控制器和软测量仪表带来的影响。由于配方数据是包含不同数据类型的大规模高维数据，而传统的聚类算法很难处理这种数据类型，本文提出一种基于子空间的聚类改进算法，实验仿真结果表明，对比于传统的高维数据子空间聚类算法，本文算法提高了子空间聚类的精度和伸缩性。对比于前人的配方聚类算法，本文算法更适合于高维的大规模配方数据。

［1］ANSI／ISA－S88.01－1995，Batch Control Part 1：Models and Terminology［S］.

［2］侯迪波，张光新，周泽魁，等.间歇生产过程配方的模糊聚类方法［J］.江南大学学报：自然科学版，2005，4（2）：33－38.

［3］陈晓芳，刘珊中.基于概率神经网络的批量生产过程配方分析［J］.化工及自动化仪表，2010，37（7）：24－27.

［4］ANSI／ISA－S88.02－2001，Batch Control Part 2：Data Structures and Guidelines for Languages［S］.

［5］Chen X，Ye Y，Xu X，et al.A feature group weighting method for subspace clustering of high－dimensional data［J］.Pattern Recognition，2012，45（1）：434－446.

［6］Duan Dongsheng，Li Yuhua，Li Ruixuan，et al.Incremental K－clique clustering in dynamic social networks［J］.Artificial Intelligence Review，2012，38（2）：129－147.

［7］Liu Guangcan，Lin Zhouchen，Yan Shuicheng，et al.Robust recovery of subspace structures by low－rank representation［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2013，35（1）：171－184.

［8］Wagstaff K，Cardie C，Rogers S，et al.Constrained k－means clustering with background knowledge［C］／／18th International Conference on Machine Learning （ICML 2001），2001：577－584.

［9］Amir A，Lipika D.Ak－means type clustering algorithMfor subspace clustering of mixed numeric and categorical datasets ［J］.Pattern Recognition Letters，2011，32（7）：1062－1069.