多分辨率多目标物流配送中心选址模型研究

崔永杰（深圳大学 土木工程学院，广东 深圳 518060）

CUI Yong-jie (College of Civil Engineering,Shenzhen University,Shenzhen 518060,China)

0 引 言

物流配送中心选址决策对整体物流配送网络的运作效率、服务水平和运营成本有着深远影响，因此如何改进和完善现有选址方法，提高配送中心选址的有效性和可靠性，成为众多专家学者研究的重点。在定性分析选址上，选址方法改进主要通过跨学科理论结合，应用更为全面准确的综合评价方法对配送中心进行分析选址[1-5]。而在定量建模选址方面，则是以传统选址模型为基础[6-7]，补充潜在选址影响因素，应用智能算法求解，使选址模型更贴合实际[8-14]。

尽管传统选址模型已得到大量改进，但仍缺乏全面性与准确性的良好综合。因此根据多分辨率建模的思想，本文结合层次分析法与混合整数规划法建立多分辨率多目标配送中心选址模型。模型首先应用层次分析法对备选配送中心进行宏观综合指标评价，确定初始选址方案。然后利用混合整数规划法综合选址成本、客户满意度等选址影响因素建立多目标选址模型，通过对模型MATLAB遗传算法求解获得最佳选址方案，从而一定程度上规避定性与定量选址方法的固有缺陷，实现配送中心选址系统准确的目标。

1 多分辨率物流配送中心选址模型

1.1 多分辨率建模概述

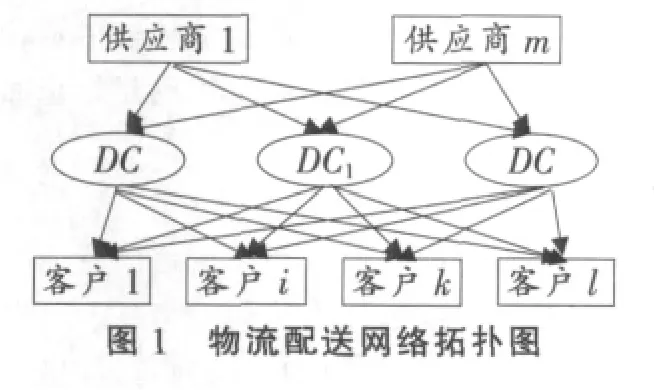
多分辨率建模 （Multi-Resolution Modeling,MRM）是指针对同一个对象或问题，通过在不同维度上建立模型，最终得到包含不同分辨率的模型或模型簇[15]。在具体应用于物流配送中心选址时，多分辨率建模可以分解为宏观、中观和微观层面选址。宏观选址应用于国家地区级选址，中观选址应用于城市区域级选址，微观选址则用于确定备选点具体位置。选址模型越接近宏观层面，其抽象程度越高，越接近微观层面，其精度要求越高。

1.2 AHP层次分析法

层次分析法 （Analytic Hierarchy Process,AHP）是应用数学方法将决策过程中的定量分析与定性分析有机结合的一种系统综合评价方法，其基本分析逻辑为：依据研究对象要求建立系统分析层次结构，描述系统功能及特征，提供相应评价标准；决策者基于上层目标对下层元素两两比较，确定下层元素对于上层目标的重要程度，即权重；分析各决策方案对总体目标的综合权重，获得各方案的综合评价值，做出最优决策[16]。

1.3 混合整数规划法建模

传统配送中心选址模型是以总成本最优为选址目标，在满足客户需求的基础上，考虑运输费用和建设费用的单目标选址规划模型。本文以传统模型为基础，综合考虑运输成本、建设成本、管理成本、环境保护和客户满意度等选址影响因素，建立以选址总成本最低和配送服务水平最优为目标的双层选址规划模型。

1.3.1 模型假设

（1）客户需求仅由配送中心满足； （2）拟建物流配送中心数目已知； （3）配送网络节点间运输距离已知； （4）配送中心基本成本信息已知； （5）客户需求量、配送时间要求及配送前置期已知； （6）单位运输成本与运量、运距成正比例关系，单位环保成本与运距成正比例关系。

1.3.2 变量说明

i：表示供应商i，其中共用n位供应商；j：表示物流配送中心j，其中共用m个配送中心；k：表示客户k，其中共用l个客户；xij,xjk：分别表示供应商i发往配送中心j，配送中心j发往客户k的货运量；cij,cjk：分别表示供应商i发往配送中心j，配送中心j发往客户k的货物单位运输费用；dij,djk：分别表示供应商i与配送中心j，配送中心j与客户k之间的运输距离；Xk：需求点的需求量；Yj：配送中心j是否被选中；Fj：配送中心j的建设费用；Cj：配送中心j的单位管理费用；Ej：配送中心j的固定环保费用；e：货物运输单位距离的环保费用；tjk：配送中心j发往客户k的运送时间；yjk：配送中心j与客户k是否存在供需关系；P：物流网络所需配送中心的数量；μjk：客户k从物流中心j获得所订货物的满意度函数； ［ETK,LTK］：客户可以容忍的获得货物的最大时间范围；：客户期望获得货物的时间。

1.3.3 目标函数

式 （1）表示配送中心选址成本最小化；式 （2）表示客户满意度最大化。

1.3.4 约束条件

其中，式 （3）表示配送中心为中转配送中心，式 （4）表示满足拟建物流配送中心数量，式 （5）表示每个客户仅由一个物流中心负责配送，式 （6）式 （7）表示配送中心与客户间供需关系以配送中心建立为基础，式 （8）表示配送中心按需配送，式 （9）表示配送中心建立决策，式 （10）表示是否与客户具有供需关系；式 （11）表示客户满意度函数。

1.3.5 遗传算法求解

遗传算法 （Genetic Algorithm）是一种模拟自然选择和群体遗传机理中自然进化过程而产生的由选择算子、杂交算子和变异算子组成的全局寻优算法，其基本计算过程为：选择编码策略，将参数集合转换为基因型结构数据；定义适应度函数；确定遗传策略；随机生成初始化群体；计算选择群体中个体位串解码后的适应度；根据遗传策略，运用选择、交叉、变异方法，生成下一代群体；判断是否满足终止循环条件，满足则解码输出结果，否则返回上步骤继续计算[17]。

2 算例分析

2.1 算例背景

某生产企业拟在华东地区新建两个物流配送中心以改善该地区配送服务。已知生产工厂位于北京、成都和深圳；华东地区配送中心候选地为杭州、南京、上海、无锡、宁波；客户则主要分布于常州、镇江、金华、嘉兴、绍兴、南通和温州等地。其中，配送网络节点间运输距离和单位运输费用，客户需求量和配送时间要求，以及备选配送中心基本费用信息已知。

2.2 AHP层次分析法选址

图2 AHP评价层次体系

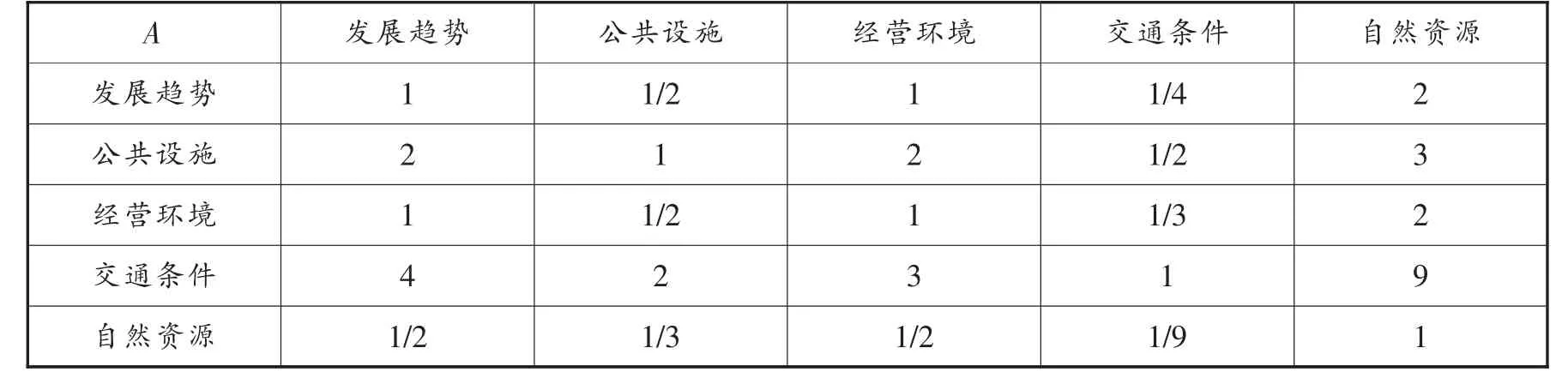
表1 目标层与准则层间判断矩阵

通过求解判断矩阵得到特征向量W=［0.119,0.226,0.127,0.463,0.062］T， 最大特征根 λmax=5.038。于是CI=（λ* max-n（n-1）=0.0095，查表RI=1.12，则CR=CI/RI=0.00848＜0.01。判断矩阵通过一致性检验，特征向量W为评价指标权重。

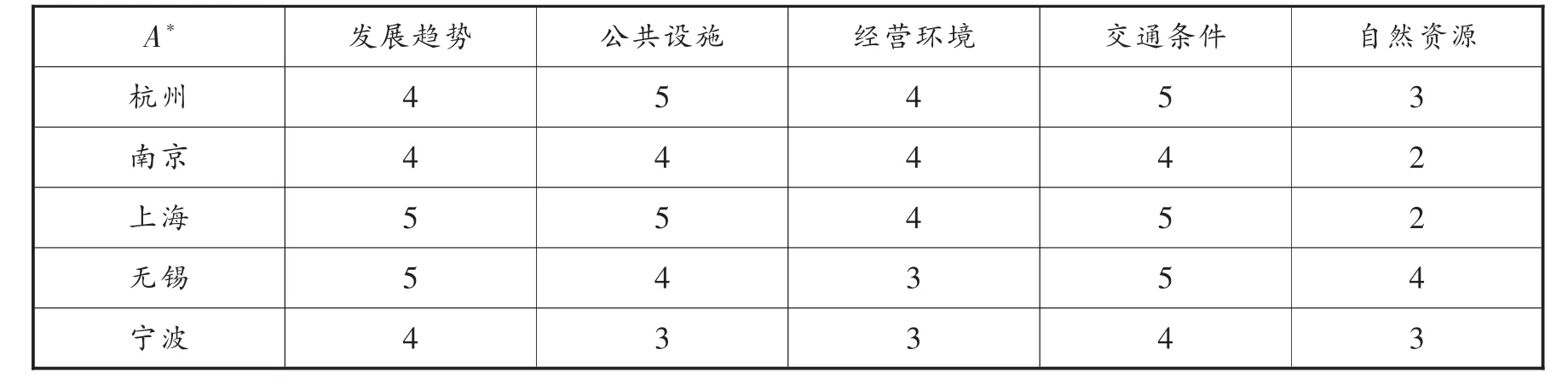
表2 备选点专家评价表

表3 备选点综合得分A**W

根据对备选配送中心的综合分析评价，选择具有相对优势的杭州、上海、无锡作为配送中心选址的初始方案。

2.3 混合整数规划法选址

表4 客户需求量

表5 配送网络单位运输费用

根据混合整数规划选址模型，确定具体遗传算法要素编码：适应度函数：@objcfun1&@objcfun2；约束函数：@con-straint；选择函数：@selection-roulette；交叉函数：@crossover-single-point；变异函数：@mutation-adaptive；种群个数：100；变量数：54；最大迭代次数：100；交叉概率：0.8；变异概率：0.005。应用MATLAB软件对要素编码求解，进而得到配送中心最佳选址方案。

表6 配送中心成本信息

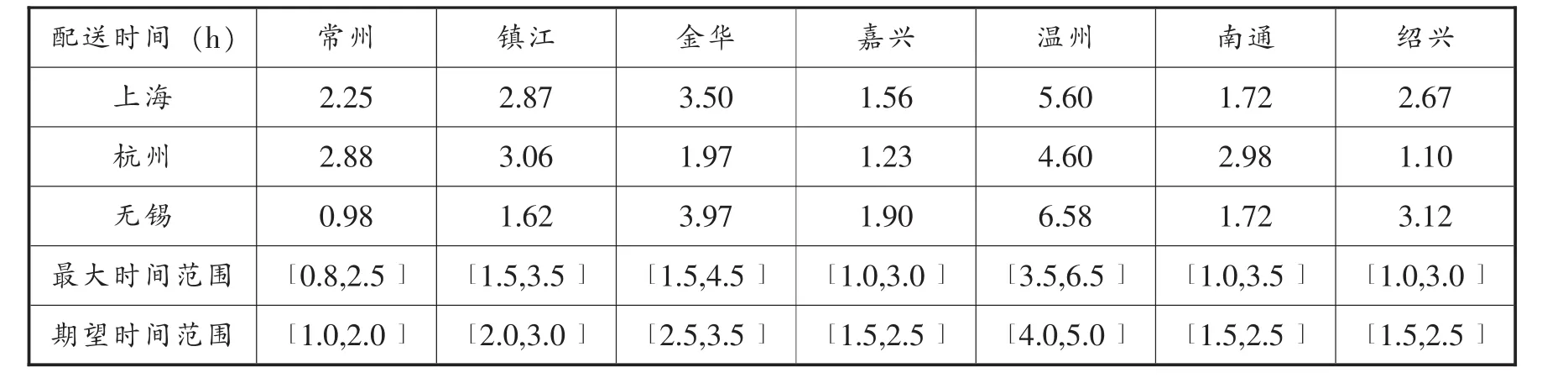
表7 配送时间及要求

表8 最终选址方案

平衡选址总成本和顾客满意度两项选址因素，杭州和无锡为物流配送中心选址最佳地点。

3 结束语

本文结合层次分析法与混合整数规划法建立了多分辨率多目标配送中心选址模型，通过宏观评价分析与微观建模求解，对备选配送中心进行筛选，逐步确定最佳选址方案。基于多分辨率建模思想建立的选址模型，能够一定程度上兼顾定性与定量选址的优点，实现可靠选址的目标，并对传统配送中心选址模型有所改进。然而本文仅考虑了单品种配送网络下的选址方案，未将配送范围、库存成本、区位优势等选址影响因素加入模型中，选址模型应用性有限。笔者将在后续的研究中进一步完善该选址模型，希望本文能够为其他配送中心选址研究提供一定借鉴作用。

[1]常艳杰.基于数学模型和AHP结合的连锁企业物流中心选址[J].物流技术，2010,29(10)：157-160.

[2]张永，李旭宏，毛海军.综合模糊品质机能法和模糊TOPSIS的配送中心选址方法[J].公路交通科技，2006,23(9)：135-139.

[3]张华，何波，杨超.基于粗糙集和多目标规划的多物流配送中心选址[J].工业工程与管理，2008,13(2)：69-73.

[4]徐斌，诸葛承祥，高健.基于信息熵—灰色关联法的物流配送中心选址模型研究[J].物流技术，2011,30(5)：116-118.

[5]Chuang P T..需求角度下层次分析法和品质机能法联合选址研究[J].国际制造技术，2011(18)：842-849.

[6]杨丰梅，卢晓珊.竞争设施选址理论与方法[M].北京：科学出版社，2010.

[7]张锦.物流规划原理与方法[M].成都：西南交通大学出版社，2009.

[8]税文兵，叶怀珍，张诗波.物流配送中心动态选址模型及算法研究[J].计算机应用研究，2010,27(12)：4476-4479.

[9]王晓博，李一军.电子商务环境下企业配送中心选址模型与算法研究[J].技术经济与管理研究，2005(5)：42-44.

[10]曾庆成，杨忠振，蒋永雷.配送中心选址与车辆路径一体优化模型与算法[J].武汉理工大学学报，2009,33(2)：267-270.

[11]Melo MT,Nickel S,Da Gama FS..动态多品种产能设施选址：供应链战略规划数学模型框架[J].计算机与运筹，2005,33(1)：181-208.

[12]HUANG Rongbing,Mozart BC Menezes,Seokjin Kim.成本不确定性对配送中心选址影响研究[J].欧洲运筹学，2012(218)：401-407.

[13]Sahan TM Dissanayake,Hayri onal.考虑驱动价格及保护储备的动态线性整数规划选址[J].生态经济，2011(70)：2225-2235.

[14]Nozick T.,Turnquist M A..双级库存分配与物流配送中心选址分析[J].交通科技，2001(37)：421-441.

[15]张丽岩，马健，孙焰.多分辨率物流选址系统研究[J].物流科技，2011,34(5)：1-3.

[16]杨保安，张科静.多目标决策分析理论、方法与应用研究[M].上海：东华大学出版社，2008.

[17]尚涛，谢龙汉，杜如虚.MATLAB工程计算及分析[M].北京：清华大学出版社，2011.