自耦变压器绕组漏磁场及涡流损耗的二维数值分析

钟 燕，刘文里，白永刚，马 健

(哈尔滨理工大学电气与电子工程学院，哈尔滨 150080)

随着变压器单台容量的不断提高，漏磁场随之增大，进而由漏磁场在变压器内引起的的涡流损耗及局部过热问题会显得更为突出。而变压器一旦出现局部过热，就会直接影响其使用寿命，甚至可能引起绝缘材料的热击穿等，给制造厂商和电力系统带来巨大的损失[1]。为了避免此类事故发生，有必要对变压器内部漏磁场和附加损耗进行分析。早期漏磁场的研究主要是通过解析法和实验模拟法来实现，由于变压器中绕组漏磁分布比较复杂，难以精确计算其涡流损耗，误差较大。从20世纪70年代起，数值方法被引入漏磁场的研究领域[2-4]。本文在总结前人工作的基础上，利用具有多物理场耦合分析和自动网格剖分功能等优点的ANSYS有限元软件，合理简化模型，采用“场-路耦合”分析方法模拟实际变压器的额定运行情况，最后得出油浸式自耦变压器绕组的漏磁场和涡流损耗分布。

1 计算原理

利用ANSYS软件中的电磁场模块对变压器的简化模型进行分析，建立绕组的实际模型，采用“场-路耦合”法计算绕组漏磁，在获得较准确的绕组漏磁场基础上，计算绕组的涡流损耗值，得到涡流损耗分布。

1.1 变压器漏磁场的计算

采用“场-路耦合”方法来模拟变压器的高-中额定运行情况。实现方法如下:在模型区内建立变压器实际模型，在模型区外建立电路模型，以模拟实际的模型区内的绕组情况。

“场-路耦合”有限元方程为

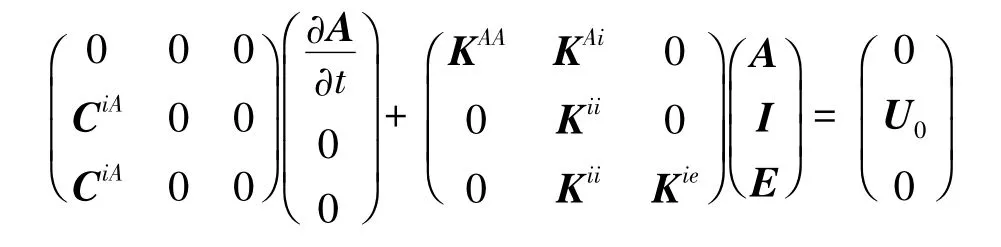
式中:A为节点的向量磁位矩阵;I为节点电流矩阵;E为节点电动势矩阵;KAA为向量位刚度矩阵;Kii为电阻刚度矩阵;KAi是磁位与电流耦合的刚度矩阵;CiA为电感阻尼矩阵;Kie为电动势与电流耦的合刚度矩阵;U0为外加电压矩阵[5]。

在圆柱坐标系中，流过绕组的电流产生的磁场满足下面的方程:

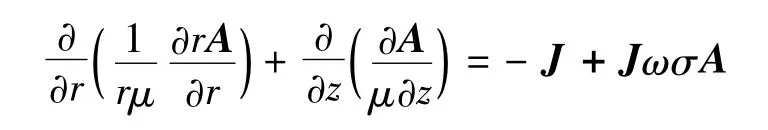
式中:μ为磁导率，H/m;σ为电导率，S/m;A为磁矢位，Wb/m;J为源电流密度，A/m2。

1.2 变压器涡流损耗的计算

变压器的漏磁场分为纵向和横向漏磁场，与之对应，漏磁通在绕组导线中所引起的涡流损耗也分为纵向和辐向涡流损耗。单位体积内的涡流损耗计算公式为

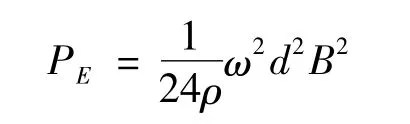
对于一个三角形单元沿圆周所构成体积内的横向涡流损耗为

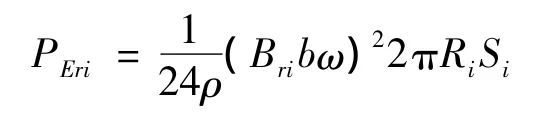
纵向涡流损耗为

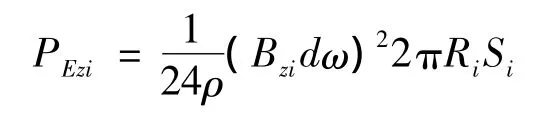
绕组总的涡流损耗为

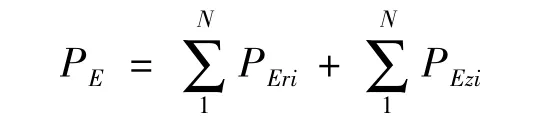
式中:Bri为第i个单元内的横向磁通密度;Bzi为第i个单元内的纵向磁通密度;ω为角频率;ρ为材料的电阻率;b、d为导线尺寸;Ri为第i个单元的重心到铁心中心线的距离;Si为第i个单元内导体所占的面积;N为绕组总单元数[6]。

2 计算实例

采用有限元法对1台ODFS-334000/500自耦变压器绕组的漏磁场和涡流损耗进行计算分析。单相无励磁调压自耦变压器绕组排布以及联结形式如图1所示，采用旁柱调压结构。所分析变压器采用的线段导线均为HQQN自粘性换位导线，主要线规为单根裸导线，厚度为1.42 mm，宽度为5.3 mm，部分技术参数如表1所示。

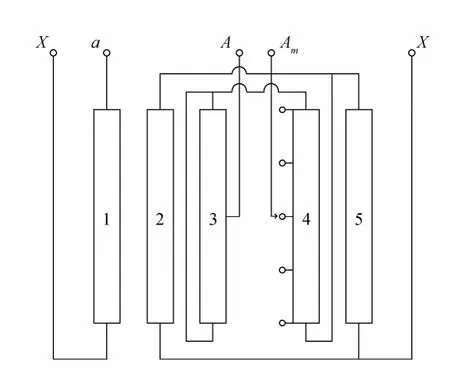
图1 旁柱线性调压自耦变压器示意图

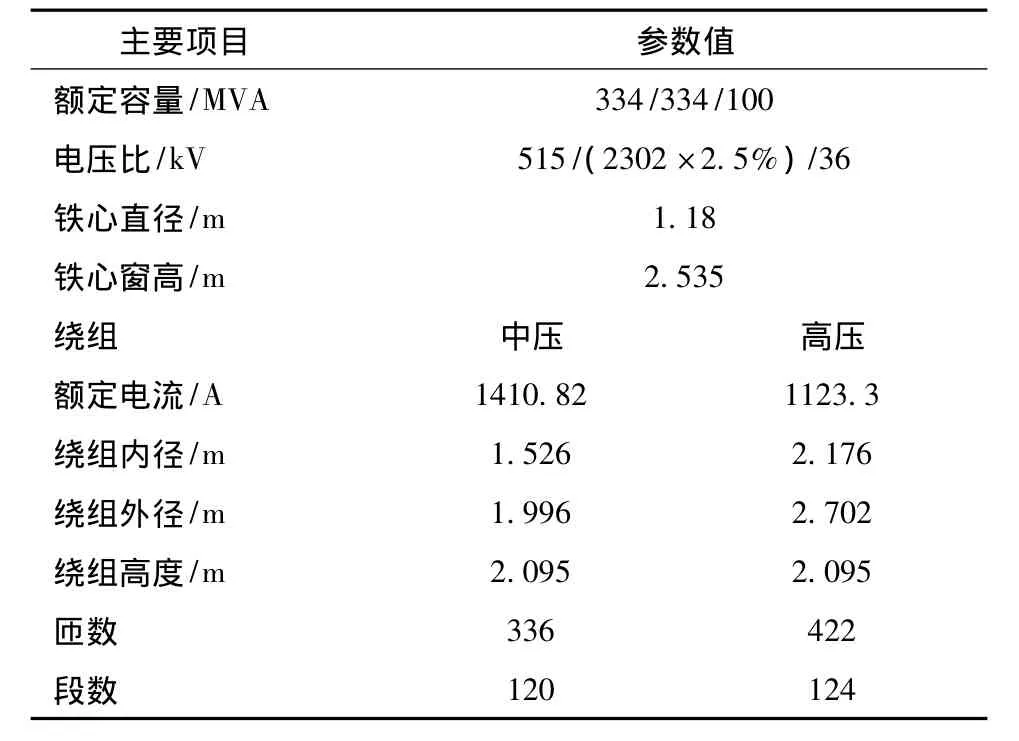
表1 变压器绕组主要技术参数

2.1 建模

变压器的漏磁场是一个三维场，根据变压器结构及运行的特点，可做如下假设:

1)漏磁场模型可以简化为二维场计算。

2)由于求解模型的对称性，故只建立剖面的一半。

3)忽略支架、拉板、夹件及绕组涡流损耗对漏磁场的影响。

4)各场量均随时间作正弦变化，不考虑高次谐波、空间电荷、位移电流的影响。

重点计算高-中额定分接运行时绕组的漏磁场，故只建立铁心窗内模型，简化模型如图2所示。绕组分饼建模，按实际尺寸建立绕组的匝绝缘、垂直油道，铁心也按实际尺寸建模。

图2 变压器部分简化模型

2.2 剖分和加载

主要计算绕组的漏磁场及涡流场，因此要对绕组细剖，采用映射剖分，其它部分采用自由剖分。

“场-路耦合”法在有限元软件中的实现方法如下:在模型区建立变压器高、中压绕组及铁芯的实际模型，高、中绕组的线饼数、线饼尺寸、垂直油道等均按实际情况建模;在模型区域外建立电压源、电压绞线圈、电阻来模拟实际的绕组运行情况。由于模拟的是高-中额定分接运行情况，所加负载也是额定分接时的额定负载。绕组电路部分模型如图3所示。

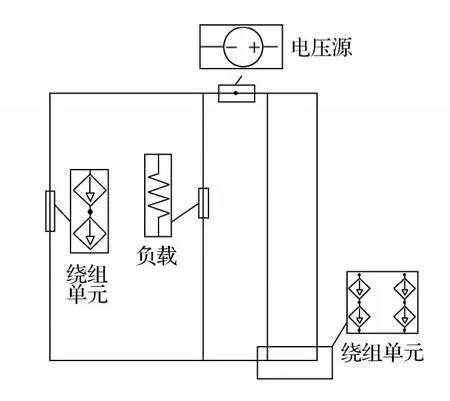
图3 绕组电路部分模型

3 仿真结果分析

采用谐波分析方法，耦合电压、电流自由度在对称轴处施加通量平行边界条件[7]，进行求解分析。

3.1 漏磁场结果分析

从ANSYS软件后处理部分得到的漏磁场结果如图4—图6所示。

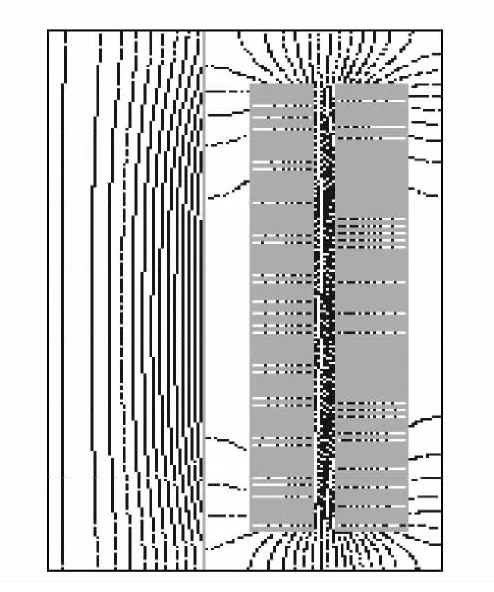
图4 磁力线分布图

图5 绕组纵向漏磁密云图

图6 绕组辐向漏磁密云图

从图4可以看到，高、中压绕组的磁力线分布上下对称，主漏磁空道之间磁力线最密，漏磁最大，在绕组端部有大量磁力线弯曲，从而会引起较大的横向漏磁。

从图5—图6可以看到，纵向漏磁在绕组中部靠近主空道处较大，但在中压绕组内侧和高压绕组外侧非常小，接近于零，而横向漏磁在绕组端部较大，中部很小。

从高-中绕组的纵向漏磁分布图7可以看到，漏磁曲线大致呈梯形分布，中间主空道漏磁最大，向两边逐渐减少至零。

图7 高、中绕组沿绕组径向的漏磁分布

高、中压绕组内、外径处沿绕组轴向高度的横向漏磁和纵向漏磁分布如图8—图11所示。

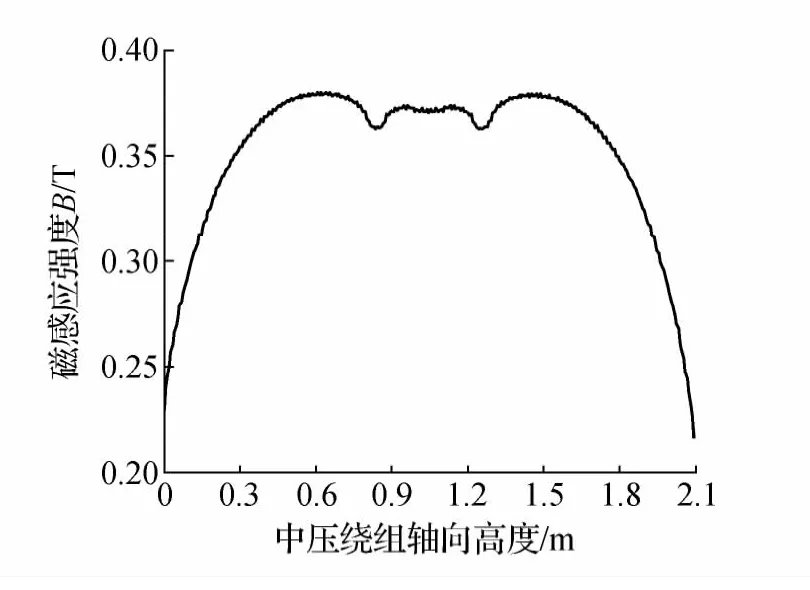
图8 中压绕组外侧纵向漏磁分布

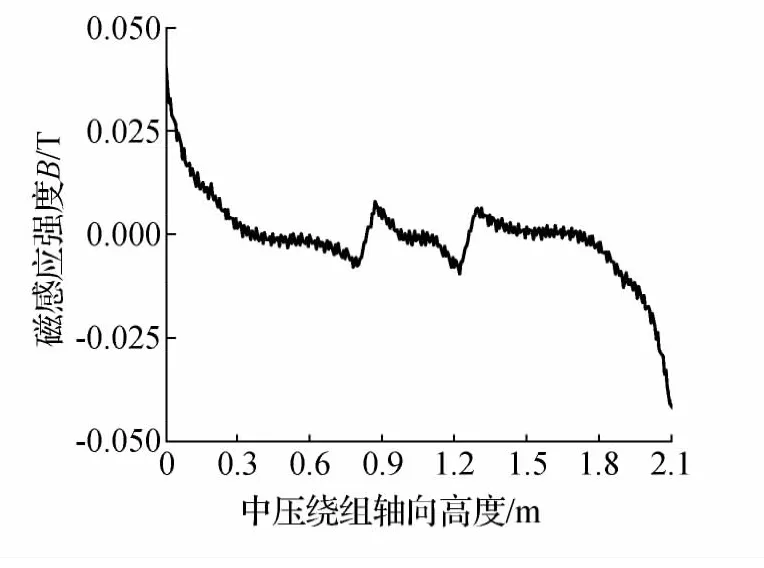
图9 中压绕组外侧横向漏磁分布

图10 高压绕组内侧纵向漏磁分布

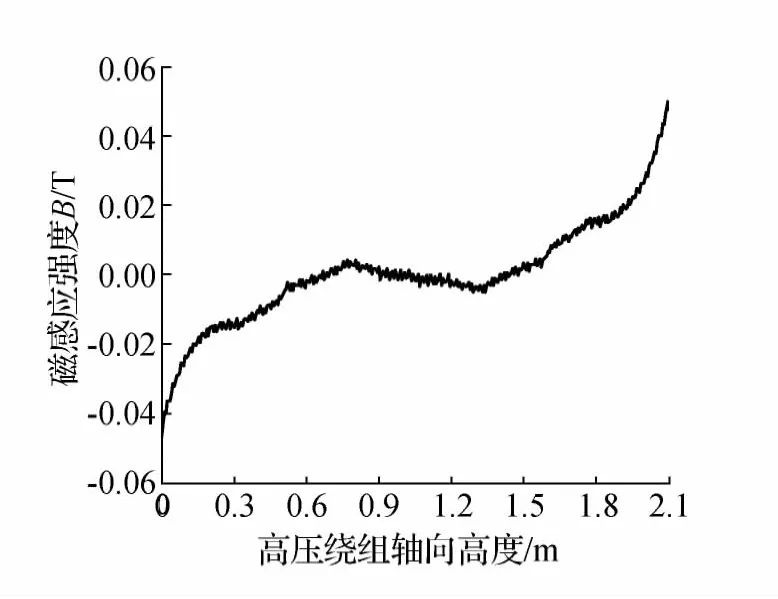
图11 高压绕组内侧横向漏磁分布

从图9和图11可以看到，高、中压绕组的端部横向漏磁较大，这是由于磁力线在绕组端部弯曲而导致的。图8和图10显示绕组纵向漏磁都是中间大两边小且有许多小的波动，这是由于高压绕组为饼式绕组，饼与饼之间都有垂直油道。又因为高压绕组采用中部出线，上下两部分完全对称，所以横向漏磁与纵向漏磁在绕组轴向高度上也是完全对称的。绕组中部附近的磁力线有向外凸出，故绕组的最大纵向漏磁不是出现在绕组中部，而是在中部的上下两侧。

3.2 涡流损耗分析

高、中压绕组电流密度分布如图12—图13所示。

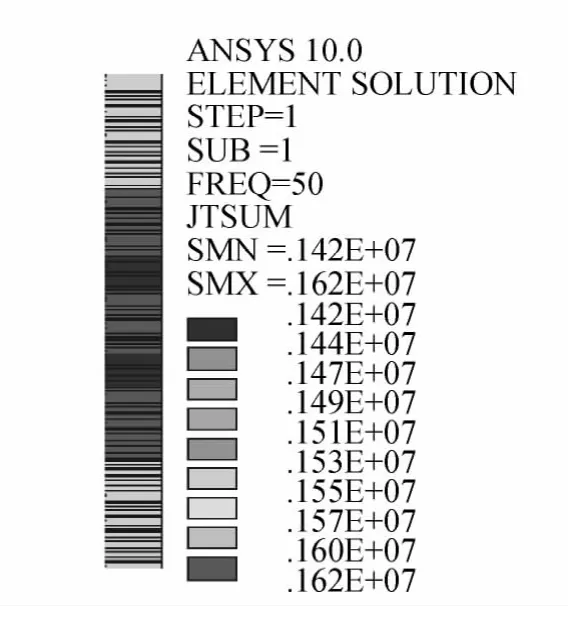
图12 高压绕组电流密度分布

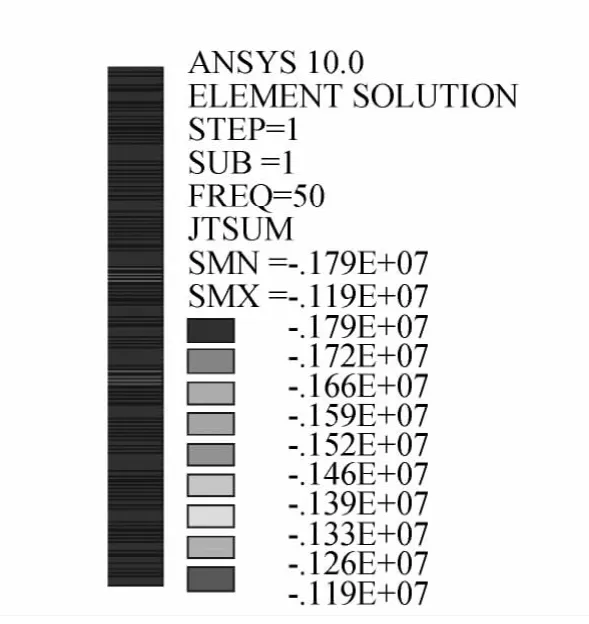
图13 中压绕组电流密度分布

从图12可以看出，高压绕组电密在端部和中部位置较大，在这些位置相应的会产生较大的涡流损耗。从图13可以看出，中压绕组中部上下两侧有四饼绕组电流密度比中部其他位置的小，在这些位置的涡流损耗也会相对较小。

3.3 计算结果分析

高、中绕组的纵向涡流损耗分布如图14和图15所示。

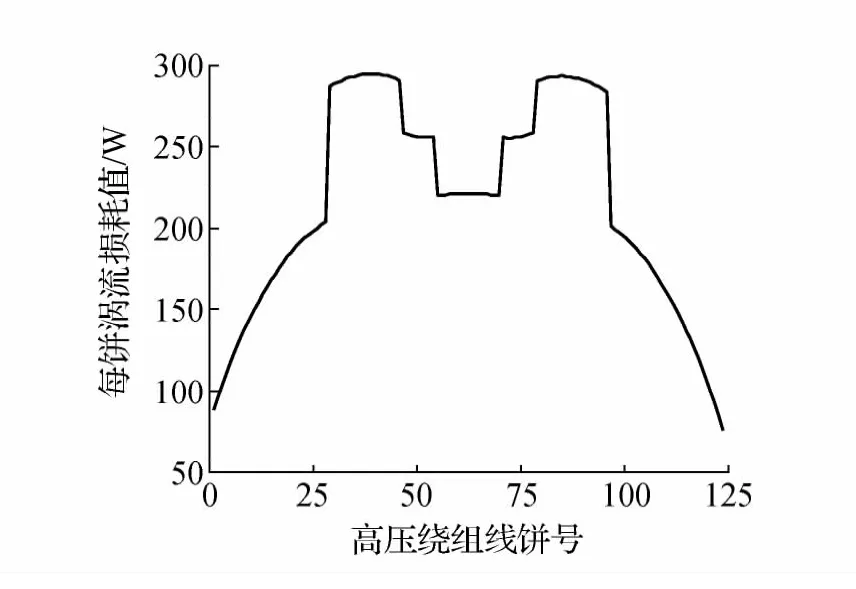
图14 高压绕组纵向涡流损耗分布

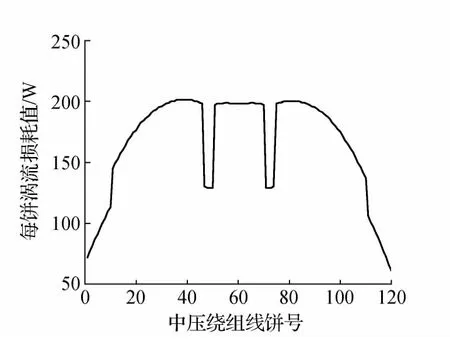
图15 中压绕组纵向涡流损耗分布

从图14可以看到，高压绕组纵向涡流损耗的最大值出现在绕组中部的上下两侧，这是因该处的漏磁较大且线段的导线厚度较大所致。从图15可以看到，中部上下两侧出现两个较明显的低点，这是因为该处的线段每段匝数少、尺寸小以及该位置的纵向漏磁相对较小所致。

高中每饼绕组辐向涡流损耗分布如图16和图17所示，最大值分别为613 W和517 W。

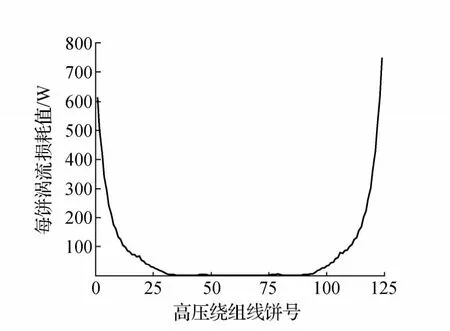
图16 高压绕组辐向涡流损耗分布

图17 中压绕组辐向涡流损耗分布

从图16和图17可以看出，高、中绕组横向涡流损耗分布趋势基本相同，均是在绕组端部有最大值，中部位置最小，且接近于零。影响横向涡流的主要因素是导线宽度和横向漏磁。有限元法算得的涡流损耗值与工程算法的值的对比如表2所示，工程算法只考虑了绕组纵向涡流损耗，而有限元法可以算得辐向和纵向涡流损耗。

表2 有限元算法和工程算法涡流损耗值的比较kW

从表2中可以看到，有限元算法的值比工程算法的值大，这是因为有限元法计算了每根导线的涡流损耗大小，而工程算法只是在简化漏磁分布的情况下得出的近似值。所以由有限元法得到绕组辐向涡流损耗约为纵向涡流损耗的1/3。这么大的辐向涡流损耗值，显然是不应该忽略的。

4 结论

通过对一台高-中运行的334 MVA油浸式单相自耦变压器的绕组漏磁场进行ANSYS有限元仿真分析，得到了绕组漏磁场的二维分布情况。通过对得出的漏磁场相关数据进行分析处理，得到了绕组涡流损耗的分布情况。将计算出的涡流损耗值与工程算法的值对比，结果基本一致，表明了ANSYS有限元计算方法的准确性，可以满足工程需要。计算出了每饼绕组的辐向和纵向涡流损耗值及最大涡流损耗集中区域，为自耦变压器漏磁场和涡流损耗的分析提供了一定的理论参考。

[1]张安红.电力变压器的损耗研究与优化设计[D].长沙:湖南大学，2005:135-136.

[2]PLONUS M，.Applied electromagnetics[M].McGraw.Hill，1978.

[3]GIRGIS R S.Calculation of Winding Losses in Shell Form Transformer for Improved Accuracy and Reliability[J].IEEE PWRD，1987，2(2):398-410.

[4]周剑明.电磁场有限元综合模拟方法及大型变压器漏磁场的研究[D].武汉:华中理工大学，1990.

[5]李晓松，胡贵，陈乔夫.基于“场-路耦合”分析的超导变压器绕组环流计算[J].电力电气，2006，25(10):21-24.

[6]康雅华.电力变压器涡流损耗和温升的计算与分析[D].沈阳:沈阳工业大学，2007.

[7]NORDMAN H，RAFSBACK N，SUSA D.Temperature responses to step changes in the load current of power transformers[J].IEEE Transactions on Power Delivery，2007，18(4):1110-1117.