基于在线小波变换的三端输电线故障定位方法

梁 捷，覃 昊

(1.广西大学 电气工程学院，南宁 530004;2.邕宁供电公司，广西 邕宁 530200)

行波故障定位法按数据来源划分主要分为两类:所需要的数据来自所有终端以及只使用本地终端数据[1]，即单端法和多端法。基于通信信道的多端故障测距算法[2]，需要采集所有终端的同步电流和本地终端的电压，多测量端数据的提取和同步的严格要求在经济上限制了其应用于多分支线路。文献[3]利用接地故障时产生的行波第一波头到达配电网线路各末端的时间进行故障定位，定位结果受网络拓扑和电网中设备的影响小，但是对上传故障信息的准确性要求较高。县级供电公司目前多采用35 kV输电线路送电，其特点是多采用树形拓扑结构，母线上连接的支路较多，常出现线路T接的情况。本文对该电压等级的三端输电系统的故障定位方法进行了研究，在分析该系统不同故障位置接收波特征的基础上，提出一种新的多端行波故障定位方法，能在不同故障位置、故障初始角和过渡电阻条件下进行故障定位，且误差较小。

1 三端输电系统故障定位算法

以故障时电气信号的高频分量作为定位判据。由于电流互感器具有较好的高频信号传送能力，而且当母线上分支较多时暂态电压信号较弱，本文选用电流行波进行故障定位。

1．1 模量转换

获取故障电流信号后，为了消除三相之间的耦合效应，采用Clark变换[4]获得电流线模分量，电流变换式如下:

1．2 在线小波变换

基于多分辨分析理论的小波分解方法通常存在时延，使得该方法无法在线使用[5]。为了从相电流的线模分量中提取故障信号的高频分量，应用了在线小波变换[6]技术，其原理如图1所示。

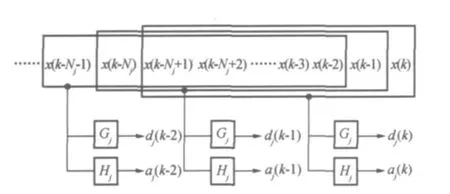
图1 在线小波变换计算原理图

假设已获取k个采样点，先设定一个时间窗，窗长N取最接近当前采样序列的长度，同时满足N=2j(j为正整数)。随着采样点数的增加，不断移动窗的位置，以纳入最新的采样点。在每个时刻，只对当前窗内的采样点进行小波分解，这样可实现任意长度信号的分解，然后根据标准同步系统通过窗重构提取同步信号，实现任意长度信号的分解，适合在线应用[5]。

式中:Aj为近似(低频)分量矩阵;Dj为细节(高频)分量矩阵;x(．)为电流信号样本;αj=2j-1;H是母波，Hii和G的计算方法参见文献[7]。与传统的小波变换相比，在线小波变换的优势在于可以同时计算每一个细节和近似分量。为了确定最好的母波和小波分解水平，进行了比较实验，结果表明，母波db4性能较好，误差小。

1．3 故障区段判定

所研究的输电线路如图2所示。lRP、lSP、lTP分别是三条支路RP、SP、TP的长度。

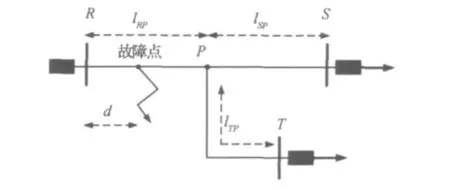
图2 三端传输线系统

确定故障区段的直观方法是比较所有终端接收波瞬时频率曲线上的首个频率突变点，即首个波头的幅值，但该法易受电磁干扰和测量装置误差影响。对此，综合考虑各端的波头，使用文献[8]的故障区段指数(Faulted Section Indices，FSI):

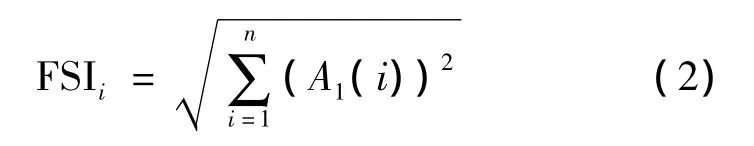
式中，A1(i)为对终端i接收波进行1尺度小波变换的细节分量幅值。

计算所有终端的FSI，然后集中比较，若满足

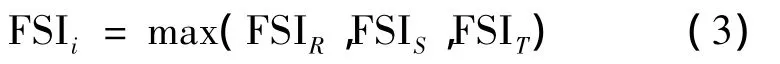
则判定终端i至T接点P之间的区段为故障区段。

1．4 确定故障信号的到达时间

故障区段确定后，可用测量故障产生的行波在故障点与母线之间往返的时间来计算故障距离。但传统的A型行波测距法存在故障波头来源难以识别的问题，如图3所示。发生在线路R-P两端对称位置的故障会有相近的接收波时差。从图3可以看出，t1-t2和t'1-t'2有近似的值，难以区分故障位置。

图3 对称故障时接收波到达情况

1.4.1 故障发生在线路的前半段

假设某故障已经发生在线路的前半段，母线接收到的第一批故障行波(对应于图3中的t1)从本地向故障点传递，然后再反射回母线，形成第二波t2，该波的总传播距离为3x。在这种情况下，第三个接收波有2种可能的情况:

1)如图4a所示，从故障点反射，此时其行进距离为5x。

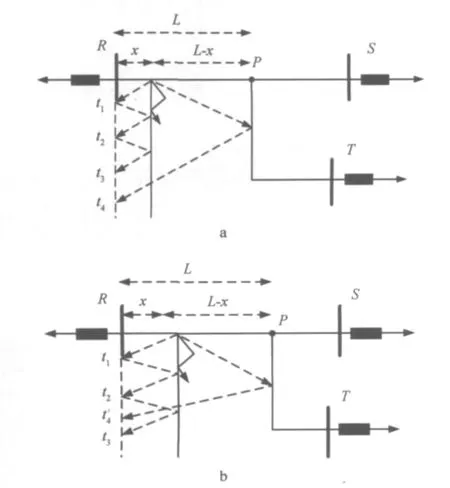
图4 故障发生在线路前半段时的可能情况

2)如图4b所示，向点P传递然后反射回本地终端，此时其行进距离为2L-x。

假设线路各点波速恒定，上述2种情况的边界条件为5x=2L-x，即x=L/3，据此讨论第三个接收波的性质。

1)x＜L/3，见图4a，此时第三波(对应于t3)由于长距离传递和故障点的额外反射损耗，比第二波的幅值更小。其小波变换结果如图5a所示，图5中IWT表示电流模量的小波变换结果。

2)L/3＜x＜L/2，见图4b，这种情况下，第三个接收波(对应于t'4)的幅值比第二波更小，见图5b。

1.4.2 故障发生在线路的后半段

在这种情况下，第二波是在P点反射并回到母线端的故障暂态信号。图6显示了在这种情况下的可能情景。

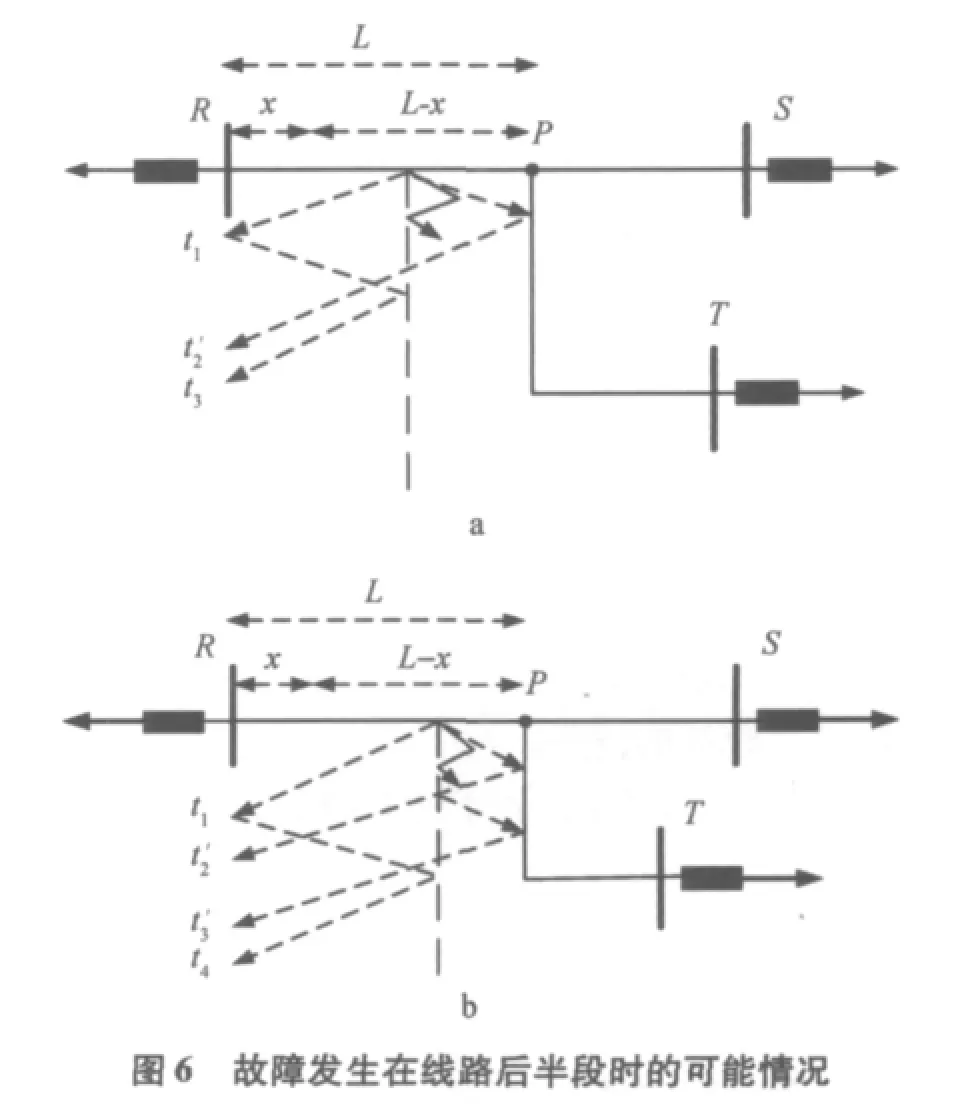
1)L/2＜x＜2L/3，见图6a，此时第三个接收波(对应于t3)的波头小于第一波，因为不考虑线路分布参数差异，第三波在故障点P反射后有一个约1/3[9]的衰减系数，但仍大于第二波。这是因为第二波(对应于t'2)是故障点发生透射时产生的。相应的小波变换结果见图7a。

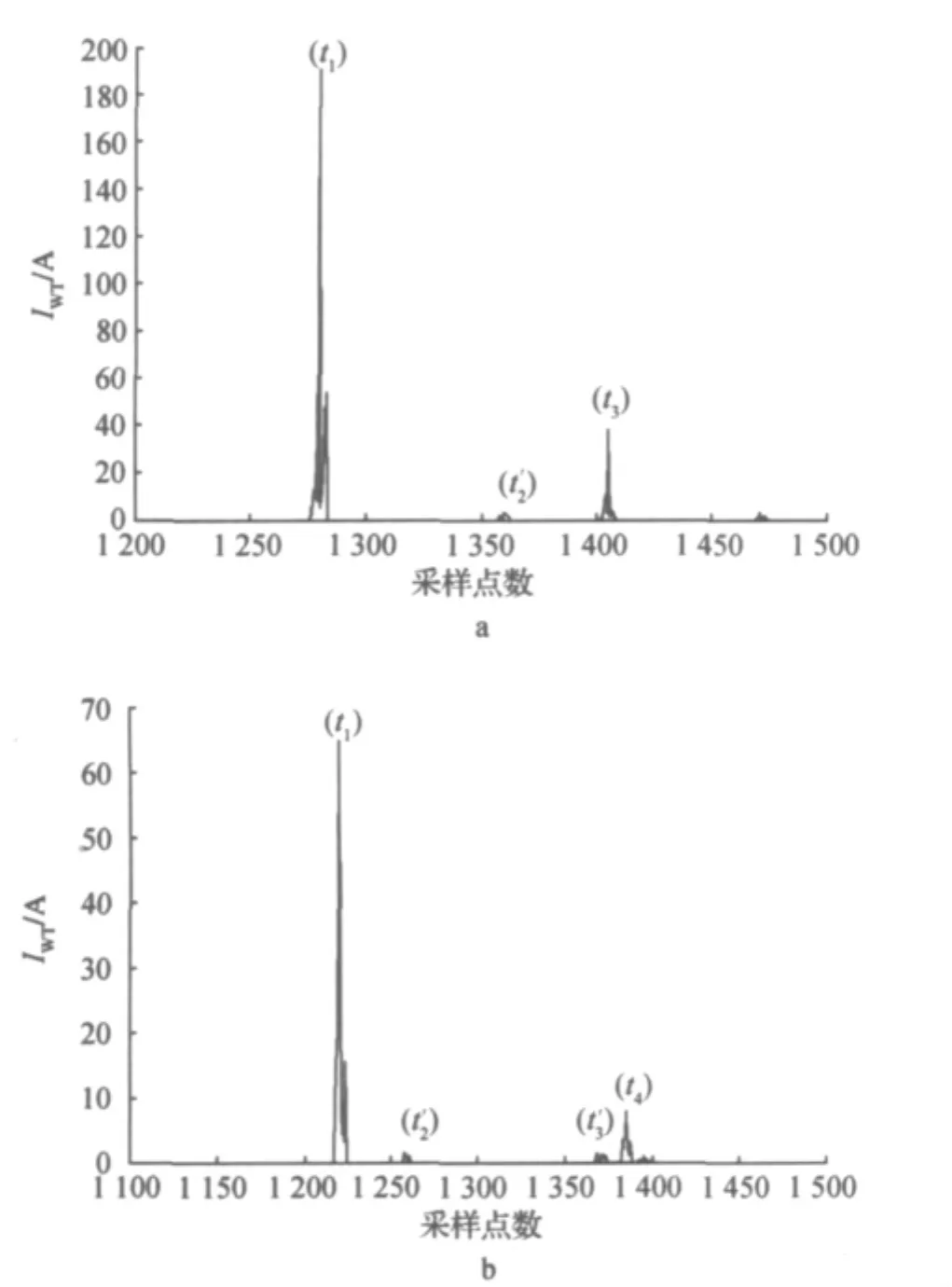
图7 R端信号的小波变换结果

2)x＞2L/3，见图6b，由于第二、第三波是透射波，第四个接收波(对应于t4)与它们相比具有较大的波头。相应的小波变换结果见图7b。

由以上4种情况可知，故障波有如下重要特征:从故障点回到测量点的第一接收波u1c和第一反射波u1f对应的小波分量具有较大的波头。为了完整显示他们，要求数据窗足够宽以包含相应线路部分至少两倍的行波传递时间(例如对终端R，窗长至少是2lRP/v1)。故障距离为

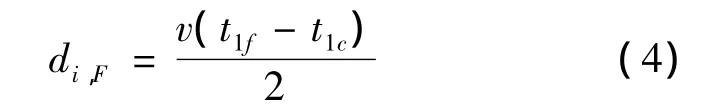
式中:v为故障行波线模分量的波速;d1，F为故障点到测量点i的距离;t1c、t1f分别为u1c和 u1f波头到达测量点的时间。

1．5 算法流程

参考图1所示线路，本方法的流程如下:

1)故障发生后，利用各终端安装的馈线终端装置(FTU)检测线路的三相暂态电流信号。

2)在合适的时间窗[6]内，根据式(1)对采样数据进行模量转换，获得线模分量。

3)将各端所得结果上传至监控中心主站集中分析，对线模分量进行在线小波变换，确定各终端第一接收波的波头。

4)按式(2)计算FSI并排序，按式(3)判定故障区段。

5)确定故障接收波u1c和u1f波头对应的时刻t1p和t2p，按式(4)确定故障位置。

2 仿真结果

为了验证所提算法的性能，在ATP/EMTP平台上模拟不同故障条件下的情况，并用MATLAB分析和实现故障判定。所用测试系统如图3所示，参数如下:

1)电源参数。系统电压为35 kV，系统频率为50 Hz。

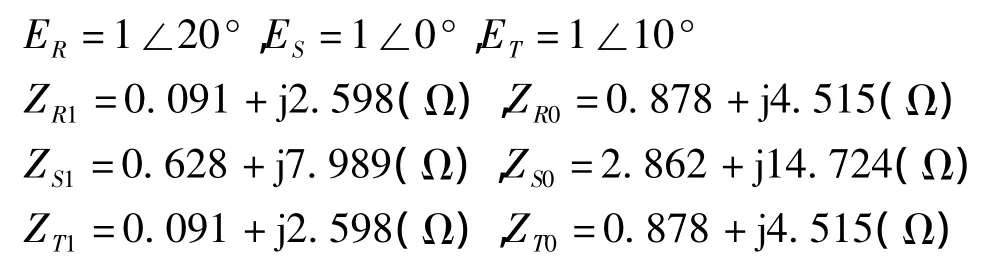
2)传输线参数为

校正[10]后 v=294117.6 km/s，不考虑线路参数对v的影响，采样频率为200 kHz。误差为

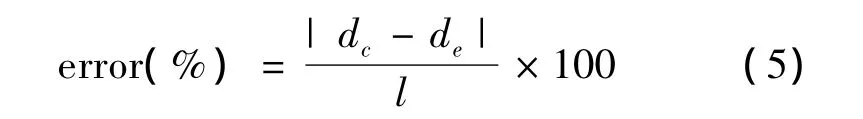
式中，dc为计算值，de为实际值，l为故障线路的最大长度。

2．1 算例分析

如图3假设在距终端R距离为120 km处发生a相接地故障(a-g)，故障过渡电阻为100 Ω，故障初始角为30°。求得每个终端的FSI如下:

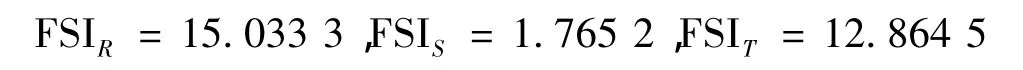
其中，FSIR的值在三者中最大，据此判断故障区域为R-P。

图8显示了终端R A相故障电流信号的小波变换结果，数据窗宽度为1.5 ms。

图8 终端R(A相)故障电流信号的小波变换结果

根据图8确定u1c和u1f的波头到达时间为

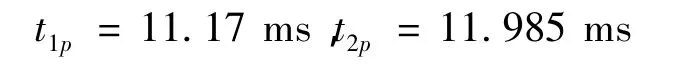
根据式(4)求得故障点至R的距离为

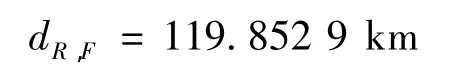
因此，由式(5)可知误差为0.058 8%，可见本方法误差较小。

2．2 不同故障位置和过渡电阻对算法的影响

图9显示了本方法在不同故障位置和故障电阻情况下发生a-g故障的定位结果。其中，故障电阻分别是1 Ω和100 Ω。

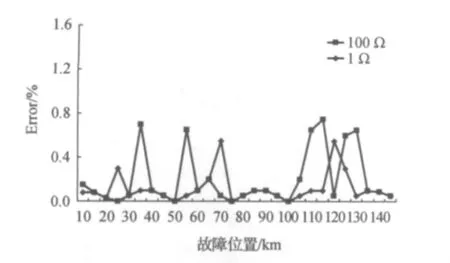
图9 不同故障位置和故障电阻下a-g故障的结果

从图9可见，本方法在不同的故障电阻和故障位置下误差均低于0.76%，定位效果较好。

2．3 不同故障初始角和过渡电阻对算法的影响

故障初相角是影响行波算法效果的重要因素[3]。不同故障初始角和故障过渡电阻时发生 a-g故障的定位结果如表1所示。从表1可知，本方法可以计算不同故障初始角和过渡电阻时的故障位置，表1中的故障估算值与实际值的偏差均小于0.8 km，即误差均小于0.32%。

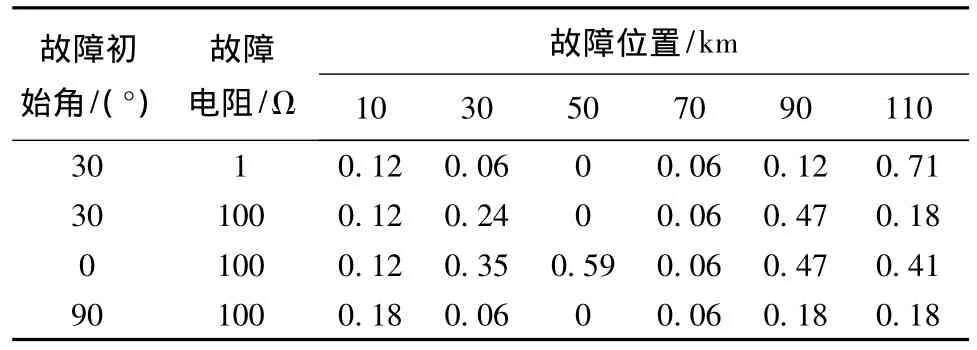
表1 不同的故障初始角和故障过渡电阻(a-g)的估算值与实际值的偏差

3 结论

提出一种三端输电系统故障定位方法。综合考虑各终端接收信号确定故障区段，利用故障信号从故障点回到测量点的第一接收波和第一反射波的波头确定故障距离。所提方法在区内不同故障位置、故障初始角以及过渡电阻的情况下，能较准确定位。但存在的问题是:当故障发生在结点附近时，故障波在故障点和测量点之间距离短，反射频繁，单端接收波之间时间间隔小，会出现识别死区。

[1]SAHA M M，IZYKOWSKI J，ROSOLOWSKI E.Fault Location on Power Networks[M].New York:Springer，2010.

[2]苏珊.基于工频通信的10kV农网故障寻址研究[D].焦作:河南理工大学，2007.

[3]贾惠彬，赵海锋，方强华.基于多端行波的配电网单相接地故障定位方法[J].电力系统自动化，2012，36(2):96-99.

[4]邹贵彬，高厚磊，李德文.基于小波变换的超高速行波保护和故障定位算法[J].继电器，2007，35(S1):68-73.

[5]丁晖，刘君华，申忠如.在线小波变换技术在气体传感器漂移故障检测中的应用[J].西安交通大学学报，2002，36(12):1219-1221.

[6]史大明，瞿海斌，程翼宇.基于在线小波变换的毛细管电泳信号滤噪方法[J].江南大学学报:自然科学版，2007，6(3):340-344.

[7]邵学广，庞春艳，侯树泉.在线小波分析与分析化学信号的在线处理[J].中国科学技术大学学报，2004，30(2):195-200.

[8]VARMA B R K，RAMANA RAO P V.A Hybrid Method for Fault Location in EHV Multi-Terminal Circuit[C]//16th National Power System Conference.Hyderabad，2010.

[9]杨鹏，宁昕，杨以涵，等.无损传输线网格线离散格式行波[J].电网技术，2008，32(19):45-49.

[10]蔡维，张雪松，刘承，等.基于PT在线注入信号及神经网络跟踪小波变换模极大值变化的配电网故障定位方法[J].继电器，2006，34(23):44-48.