基于改进量子进化算法的变电站选址方法
2013-09-01柳双林陈华丰杨志刚
柳双林 陈华丰 杨志刚
(1.西南交通大学电气工程学院,成都 610031;2.浙江省余姚市供电局,浙江 余姚 315400)
近年来,随着经济的快速发展,供电负荷不断增加,迫切地需要在已有变电站的基础上,增建新的变电站以满足负荷需求。变电站站址的优化是城市电网优化的一个重要的环节,站址选择的好与坏直接影响工程投资效益,其结果直接影响未来电力系统的线路走线、网络结构、电网投资、运行经济性、供电可靠性及电能质量等[1]。
目前,变电站选址定容的研究领域有很多优化算法,大致可以划分为启发式优化方法、数学优化方法和基于随机优化方法3大类[2-3]。但是,变电站选址属于大规模复杂优化问题,问题规模一般较大,采用传统的方法求解速度慢,且解的精度较低。
量子进化算法(QEA)是最近几年发展起来的新的智能进化算法,该方法具有简单易实现、搜索精度高、搜索速度快等优点,其在求解复杂组合优化问题方面具有其他随机优化方法难以比拟的优点[4-6],本文首次把QEA引入到变电站选址模型中。但传统的量子进化算法局部搜索能力较弱,本文提出一种改进的量子进化算法(IQEA)并应用到变电所选址优化中。
本文对QEA的修复操作和进化方向进行改进,修复操作采用贪心修复,进化方向以适应度值作为吸引子进行下一代的更新。背包问题测试表明本文的改进措施增强了QEA的寻优质量,把IQEA应用到实际算例中进一步证明了本文所提出算法的有效性。
1 变电站选址模型
变电站选址问题是一个复杂的多目标优化问题,其影响因素多且复杂。一般情况下,变电站的优化配置是保证一定可靠性水平,满足规划年负荷要求条件下,以最小的投资费用确定变电站个数和位置。本文不但考虑了线路的网损费用和年投资费用,而且还加入了地理信息因素,将其量化为惩罚因子加入到目标函数中。
在优化选址之前,新建变电站的容量已经确定,新建变电站的运行费用和投资费用固定。变电站选址优化模型可以简化为只考虑网损费用和线路投资费用的方程[7],如式(1)所示。

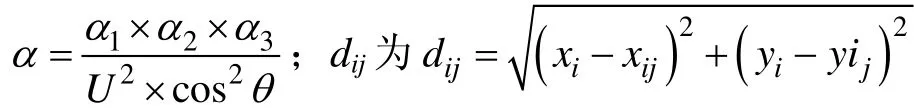
2 改进的量子进化算法
针对上述变电站选址问题,本文给出了 IQEA的变电站选址优化方法。
QEA[8-10]是一种以量子计算和进化算法相结合的概率搜索方法,它有着收敛速度快,全局搜索能力强的特点[11-13],但其局部搜索能力较弱。本文主要对传统量子进化算法的修复操作和进化方向进行了修改,来增强其寻优能力。QEA的进化方向是以适应度值作为评价的标准,以适应度值作为吸引子进行下一代的更新,文献[14-15]采用随机修复操作,并对QEA的进化方向进行改进,以优秀群体统计分析后构建整个种群的吸引子,使得进化方向更加合理、科学。本文在其基础上对修复操作进行修改,采用贪心修复,并采用背包问题来测试所提出的算法。
随机修复全过程:
Step1 给 knapsack-overfilled(背包超重参数)赋值为false;
Step3 while knapsack-overfilled为true时,begin从背包中随机选择第i个物品,令xi=0,≤C,then knapsack-overfilled赋值为false,end;
Step4 while knapsack-overfilled为false时,begin从背包中随机选择第j个物品,令xj=1,>C,then knapsack-overfilled赋值为true,end;
Step5xj赋值为0;
End。
贪心修复全过程:
Step1 计算每个物品的价值密度P/W,(P为物品的价值,W为相应物品的重量);
Step2 根据上面计算的价值密度结果,对物品价值密度进行非递增排序(如果两个物品的价值密度相同,则将重量小的排在后面);
Step3 将排序后的物品按从大到小依次装入背包中,对于当前物品i,若背包剩余重量大于等于第i个物品的重量,则将物品i装入背包,继续考虑下一个物品i+1,重复Step3,直到大于或等于背包容量为止;
End。
IQEA算法流程:
Step1 初始化种群Q(0)、概率ε和学习率λ;
Step2 观测种群Q(0)得到C(0);
Step3 修复操作;
Step5 记录C(0)中最佳个体Cbest(0);
Step6 令每个个体的b(0)等于C(0);
Step7 While非结束状态do;
Step8t=t+1;
Step9 观测种群Q(t-1)得到C(t);
Step10 修复操作;
Step12 利用量子旋转门[18]和A(t-1)更新Q(t);
Step13 保存C(t)中最佳解到Cbest(t);
Step14 保存b(t-1)和C(t)中较大者为b(t);
Step15 利用b(t)和Cbest(t)生成K;
Step16 由ε、λ和K生成A(t);
End;
End。

表1 量子旋转角取值
向量K的kj分量计算公式为

式中,N为被选择种群中优秀个体的统计个数。
本文采用截断方法对个体进行统计,首先,按照适应度值对所有个体进行非升排序,其次,选取种群前η(t)的个体进行统计。
迭代时按PBIL[16]概率更新K的kj分量

概率向量K初始化为(0.5, 0.5, …, 0.5)。
吸引子A(t)的构造过程如下:
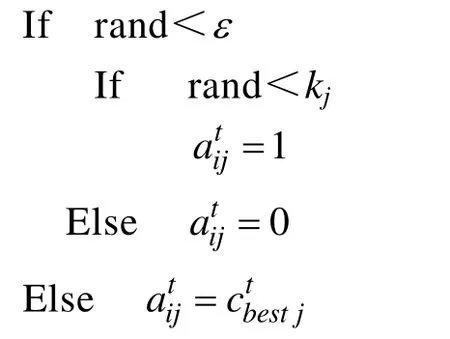
文献[17]是最新出现的对 QEA进行改进的文章,文中方法是背包问题领域中具有代表性的成果。因此,在本文的背包测试实验中以该文献中的方法作为比较方法,以测试本文 IQEA的优越性。文献[17]中的算法简称为 QIEA,文献[18]中运用随机修复的改进量子进化算法简称IQEA1,本文中运用贪心修复的改进量子进化算法简称为IQEA。背包问题数据均来自文献每次增加 200,各参数设置如表 2所示。三种算法对每个背包问题独立运行30次,分别记录最好值,最差值,平均值及方差,实验结果如表3所示。

表2 参数设置信息表
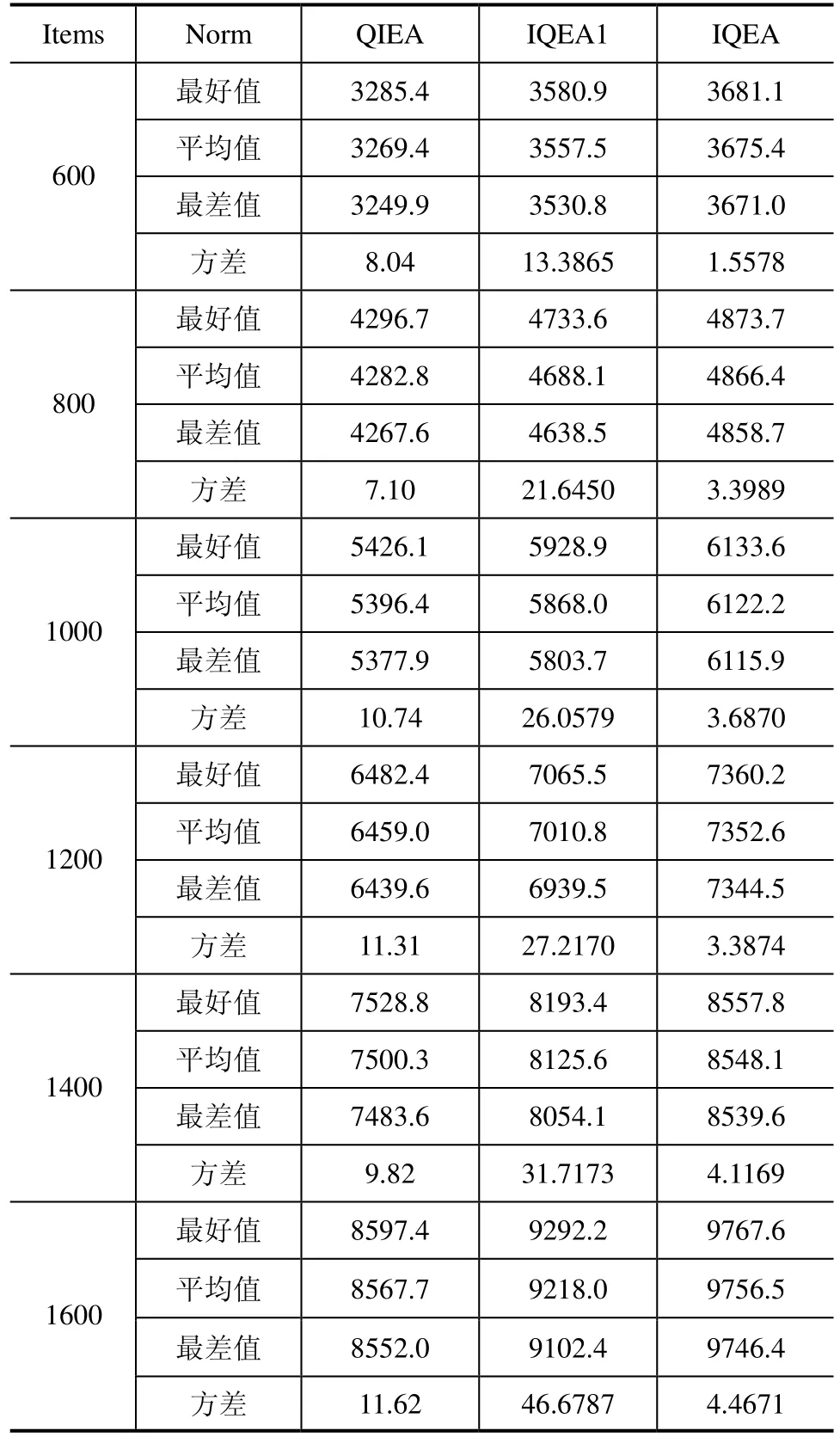
表3 背包问题实验结果
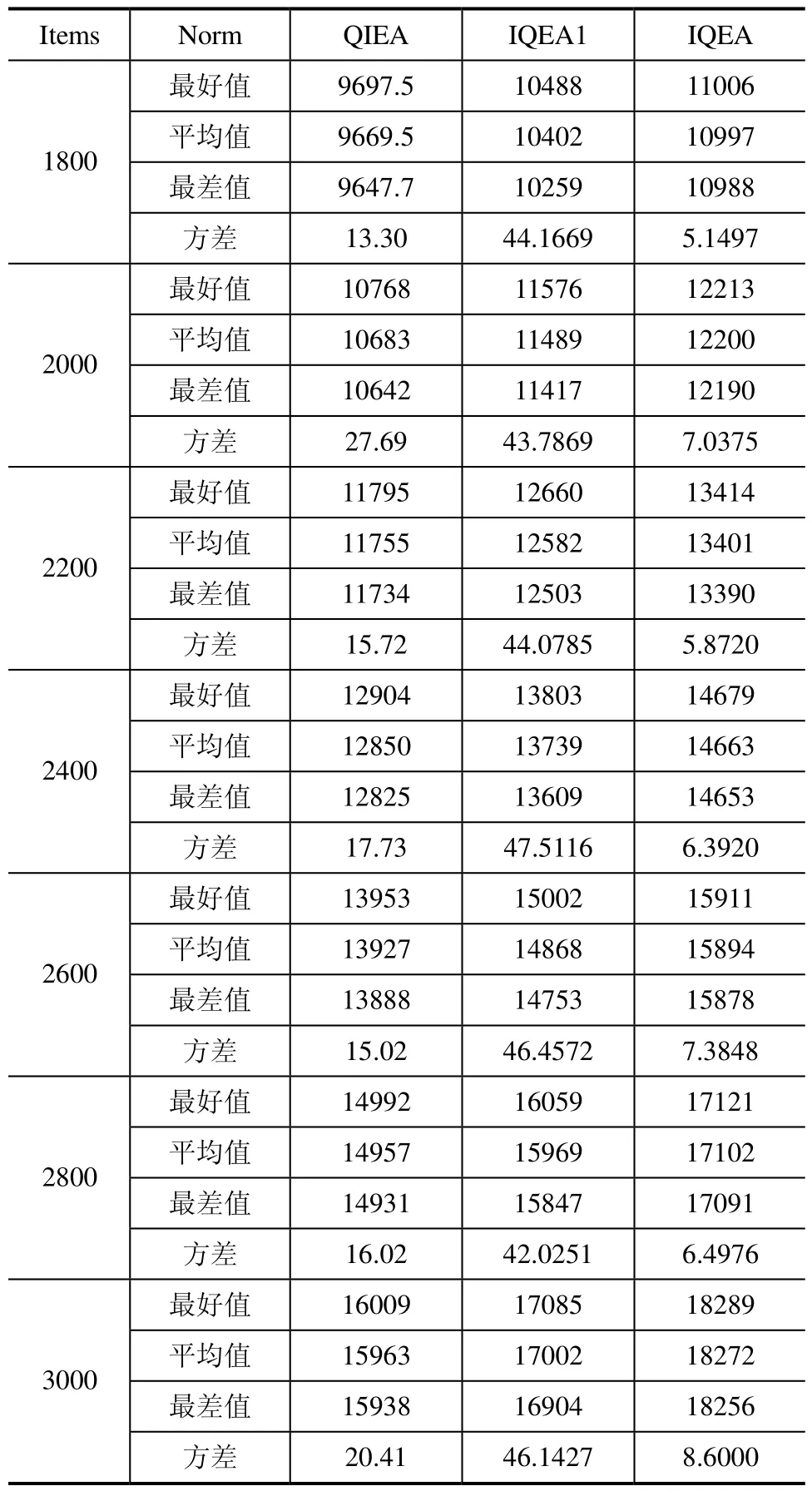
(续)
由表3的统计结果可知,IQEA的最好值、平均值和最差值3个参数值要全面优于IQEA1和QIEA。并且IQEA的方差比IQEA1要小,说明IQEA独立运行30次的结果比较稳定。因此本文IQEA的改进是合理的,具有更强的搜索能力。
3 算例应用
根据电网规划,计划建一座规模为 1×50MW的变电站(记为变电站1)和一座规模为2×50MW的变电站(记为变电站 2),用电区域共分为 10个用电单元,根据要求需要确定各个变电站的供电范围和各个变电站的最优位置,各个参数基本信息如表4所示,用电负荷点的基本信息如表5所示,相关的地理约束的基本信息如表6所示[20]。
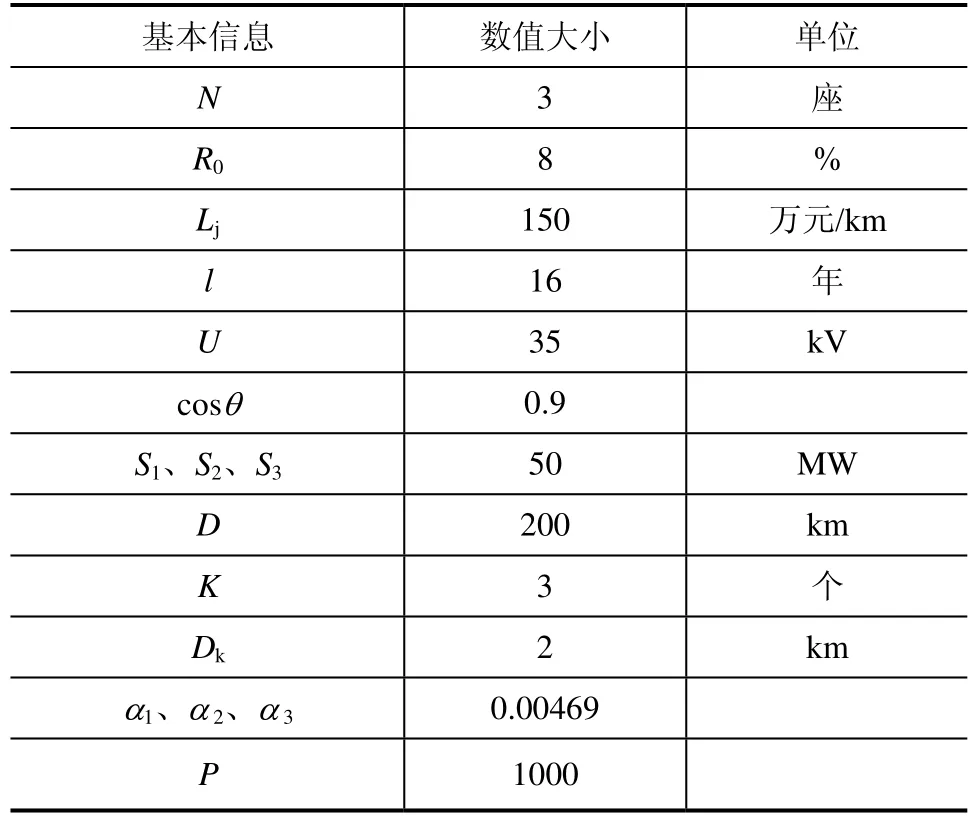
表4 参数设置信息表
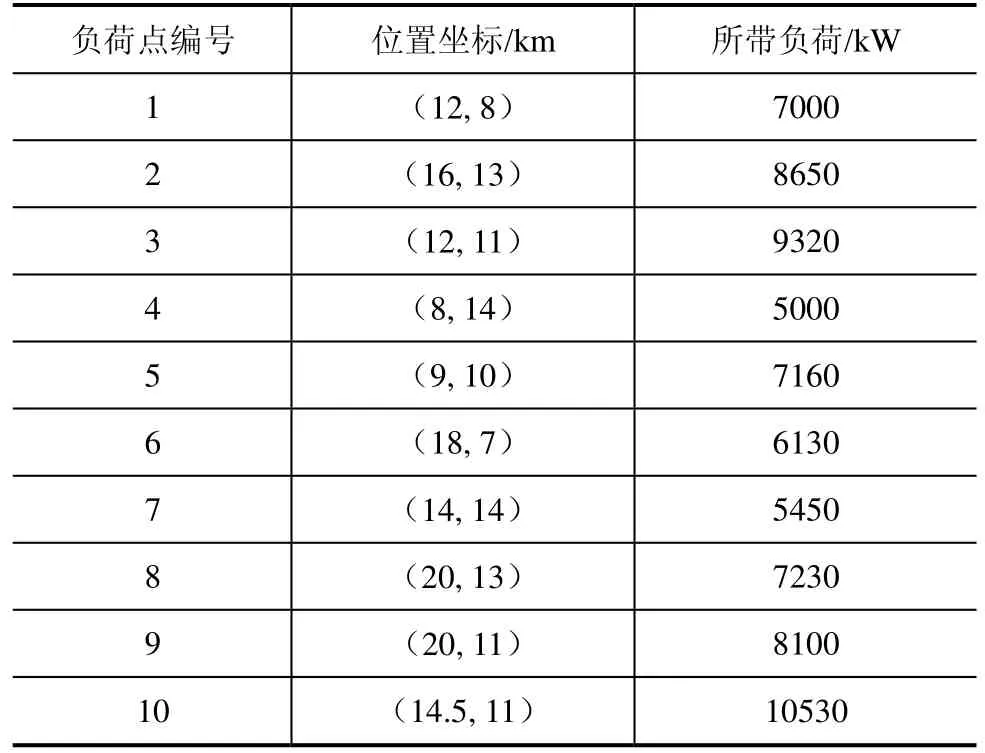
表5 用电负荷信息表

表6 地理约束信息表
由以上背包问题测试结果表明,IQEA的性能最优,因此根据变电站选址模型,分别应用基本QEA和 IQEA对变电站进行选址操作,对比寻优能力。设种群数量为10,最大迭代次数为300,优化结果如表7所示。

表7 多源变电站选址优化结果
由于,多源变电站选址优化问题是一个多目标、多约束的复杂优化问题,本文针对多源变电站选址中的二源变电站选址进行测试。由表5测试结果可知,IQEA的搜索精度要高于基本QEA,有效避免了陷入局部极值,IQEA方法比基本QEA方法节约资金 30.0377万元,新建变电站站址基本上都在负荷中心,且满足了对负荷就近供电的原则,并且IQEA优化得出的变电站1和变电站2的容载比分别为1.66和2.25,比例值满足电网容载比要求。
4 结论
变电站选址优化是一个复杂的多目标、大规模组合优化问题,本文首次将 QEA引入到变电站选址中,并提出了IQEA。IQEA对QEA的修复操作和进化方向进行改进,背包测试结果表明,IQEA的改进措施提高了搜索的精度,同时应用到具体算例中表明,IQEA是一种科学、合理的变电站选址方法。
[1] EL-FOULY T H M, ZEINELDIN H H, EL-SAADANY E F, et al.A new optimization model for distribution substation sitting, sizing, and timing[J].International Journal of Electrical Power and Energy Systems, 2008,30(5): 308-315.
[2] 刘自发,张建华.基于改进多组织粒子群优化算法的配电网络变电站选址定容[J].中国电机工程学报,2007, 27(1): 105-111.
[3] 王成山,刘涛,谢莹华.基于混合遗传算法的变电站选址定容[J].电力系统自动化, 2006, 30(6): 30-34, 47.
[4] 段刚,余贻鑫.电力系统NP难问题全局优化算法的研究[J].电力系统自动化, 2001, 25(5): 14-18.
[5] 刘建明,李茂军.基于改进遗传算法的水电经济调度[J].电力系统及其自动化学报, 2007, 19(5): 39-44.
[6] 李运华,吴宏昺,盛万兴,刘科研.分布式并行混合遗传算法在无功优化中的应用[J].电力系统及其自动化学报, 2008, 20(2): 36-41.
[7] 王成山,魏海洋,肖峻,谢莹华,王凯军.变电站选址定容两阶段优化规划方法[J].电力系统自动化, 2005,29(4): 62-66.
[8] HAN K H, KIM J H.Quantum-inspired evolutionary algorithms with a new termination criterion,Hζ gate,and two-phase scheme[J].IEEE Transaction on Evolutionary Computation, 2004, 8(4): 156-169.
[9] LI Y Y, ZHAO J J, JIAO L C.Quantum- Inspired evolutionary multicast algorithm[A].Proceeding of 2009 IEEE International Conference on Systems, Man,and Cybernetics[C].USA: IEEE press, 2009.1496-1501.
[10] JIAO L C, LI Y Y, GONG M G, ZHANG X R.Quantum-inspired immune clonal on Systems, Man,and Cybernetics, Part B, 2008, 38(5): 1234-1253.
[11] 钱洁,郑建国,张超群,王翔,阎瑞霞.量子进化算法研究现状综述[J].控制与决策, 2011, 26(3): 321-326.
[12] 王凌.量子进化算法研究进展[J].控制与决策, 2008,23(12): 1321-1326.
[13] ZHANG G X.Quantum-inspired evolutionary algorithm: a survey and empirical study[J].Journal of Heuristics, 2011, 17(3): 303-351.
[14] DEFOIN P M, STEFAN S, NIKOLA K.Quantuminspired evolutionary algorithm: a multimodel EDA[J].IEEE Transactions on Evolutionary Computation, 2009,13(6): 1218-1231.
[15] 谭立湘,郭立.基于全面学习的量子分布估计算法[J].模式识别与人工智能, 2010(3): 314-319.
[16] 周雅兰,王甲海,印鉴.一种基于分布估计的离散粒子群优化算法[J].电子学报, 2008, 36(6): 1242-1248.
[17] VLACHOGIANNIS J G, Lee K Y.Quantum-inspired evolutionary Algorithm for real and reactive power dispatch[J].IEEE Trans.Power Syst.2008, 23(4):1627-1636.
[18] 钱洁,郑建国.采用群体统计学习的量子进化算法[J].西安交通大学学报, 2012, 46(2): 51-58.
[19] QIN Y H, ZHANG G X, Li Y Q.A comprehensive learning quantum-inspired evolutionary algorithm[J]//Communications in Computer and Information Science,2011, vol.268: 151-157.
[20] 董永峰,杨彦卿,宋洁,顾军华,颜威利.基于改进粒子群算法的变电站选址研究[J].继电器, 2008, 36(5):32-35.
