层次分析法在引江济汉工程渠线比选中的应用

邹 勇，董忠萍

(湖北水利水电规划勘测设计院，湖北 武汉 430064)

0 引言

引江济汉工程为南水北调中线工程的组成部分，为大型的引调水工程，引水线路西起长江龙洲垸，东至汉江高石碑，调水流量350 m3/s，年均引水量为22.8亿m3。工程区位于汉江平原腹地，跨荆州市、荆门市及潜江市三个行政区。

本工程共规划了9 条比选线路，进水口有三个:枝江大埠街、荆州龙洲垸、沙市盐卡;出水口有两个:潜江高石碑、红旗码头。在淘汰了劣势比较明显的5 条渠线方案之后，选取优劣不明显的4 条渠线方案进行进一步比选。即:龙高Ⅰ线、龙高Ⅱ线、高Ⅱ线、盐高线。

1 层次分析法简介［1］

层次分析法(The analytic hierarchy process)简称AHP 法，在20世纪70年代中期由美国运筹学家托马斯·塞蒂(T.L.Saaty)正式提出。它是一种定性和定量相结合、系统化、层次化的分析方法。

层次分析法的基本思想是:根据多目标决策问题的性质和总目标，把问题本身按层次进行分解，构成多目标决策问题的性质和总目标，构造一个由下而上的递阶层次结构。最高层为解决问题的总目标，称为目标层;若干中间层为实现总目标所涉及的中间措施、准则，称为准则层(若有多个中间层，则准则层之下为子准则层，或称为指标层);最底层为解决问题所选用的各种方案，称为方案层。相邻上下层元素之间存在着特定的逻辑关系，将上层次的每一个元素同它有着逻辑关系的下层元素用直线连接起来，就构成了递阶层次结构模型。

对于一个决策问题，分成有序的层次结构以后，对每一个上层元素，考虑与其有逻辑关系的下层元素，并在它们之间进行两两比较判断，判断的结果用定量数字给出，并表示在一个矩阵中，这样的矩阵称为“判断矩阵”。从判断矩阵的最大特征值及其特征向量，确定每一层次中各元素的相对重要性排序的权值。通过对各层次的综合，进而给出对目标层而言方案的总排序权重，并依此来确定最优方案。

2 各渠线主要特征及优缺点

2.1 比选渠线的主要特征

4 条比选渠线主要特征见表1、表2。

表1 各线路方案主要参数表Table 1 The main parameters of various line schemes

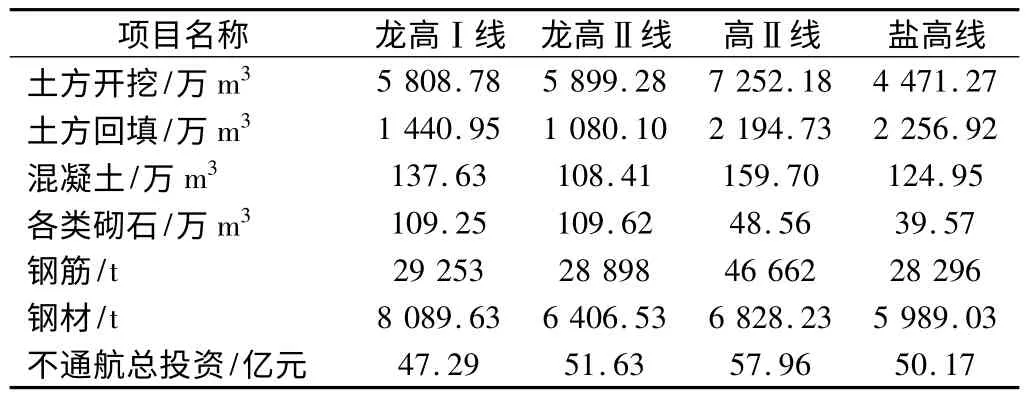
表2 各线路方案的主要工程量表Table 2 The main engineering quantities of various line schemes

龙高Ⅰ线:进口为荆州龙洲垸，出口为潜江高石碑，渠首位于荆州市李埠镇龙洲垸长江左岸，干渠渠线沿北东向穿荆江大堤、318 国道、宜黄高速公路后，以近东西向穿过庙湖、荆沙铁路、襄荆高速、海子湖后，折向北东向穿拾桥河、穿长湖、殷家河、西荆河后，在潜江市高石碑镇北穿过汉江干堤入汉江。

龙高Ⅱ线:进口为龙洲垸，出口为高石碑，龙洲垸—海子湖段、彭冢湖—高石碑段与龙高Ⅰ线重合，中段利用长湖作为调节水库，长湖—高石碑段的进水口位于毛李镇李家湾长湖边。龙洲垸—海子湖段渠道长21.65 km，长湖—高石碑段渠道长21.85 km，加固长湖围堤长47.27 km。

高Ⅱ线:进口位于枝江市七星台镇大埠街，干渠向东穿过下百里洲、沮漳河、荆江大堤，从荆州城北边穿过沪渝高速公路，然后向东偏北穿过庙湖、荆沙铁路、襄荆高速、海子湖及拾桥河后，经过蛟尾镇北，穿长湖、殷家河、西荆河，在潜江市高石碑镇北穿过汉江干堤入汉江。

盐高线:进口为沙市盐卡，出口为高石碑。渠首穿荆江大堤后，渠线沿东北向穿西干渠、沪渝高速公路，在文岗入长湖、穿西荆河，于高石碑镇北穿汉江干堤入汉江。

2.2 选线原则及各线路优缺点［2］

选线原则:①进出口位置条件优越;②尽量减少开挖工程量，减少弃渣占压土地;③尽可能避开密集居民点，减少拆迁量;④尽可能避开江汉油田及其它工矿企业;⑤尽可能绕过国家重点文物保护单位纪南城与楚汉墓葬群等;⑥尽量避开现有公路、高压线等;⑦尽量做到渠道不淤或有利于建设冲沙、沉沙设施;⑧渠深合适，有利于渠道纵坡及不同地质条件的边坡设计;⑨尽量避开不利地质条件，减少地基处理工程量。

各比选渠线优缺点见表3。

3 运用层次分析法对备选方案进行比选

3.1 建立层次结构模型

渠线比选涉及到的因素众多，且相互关联，是一个复杂的系统工程。针对这类复杂的决策问题，首先对问题所涉及的因素进行分类，然后构造一个各因素之间相互联结的层次结构模型。因素分类如下:

表3 各线路方案的主要优缺点表Table 3 The main advantages and disadvantages of various line schemes

(1)目标类，渠线比选的目的是从4 条渠线中选择一条综合效益最佳的线路，即为目标层(A)。

(2)措施类，4 条备选方案构成了递阶层次结构模型的最底层，即方案层(D)。4 个方案依次为龙高Ⅰ线(D1 方案)，龙高Ⅱ线(D2 方案)，高Ⅱ线(D3 方案)，盐高线(D4 方案)。

(3)准则类(或制约因素类)，对于这种大型的引调水工程来说，决策问题比较复杂，准则类可分解为若干层次，或称之为中间层。本层次结构模型的中间层由准则层和指标层构成。根据设计目的，遵循选线原则，确定将自然条件、经济指标、综合利用、环境影响、社会效益五个要素作为层次结构模型的准则层(B)。将上述五个要素展开，自然条件细分为进口水位与河势、工程地质条件、自流条件;经济指标展开为工程投资、技术经济指标、年运行费用三个方面;防洪灌溉、发电、通航、旅游构成评价综合利用的要素;环境影响从泥沙沉积与生态改善两方面着眼;社会效益体现在地方经济与移民安置两处。展开后的十四个因子构成层次结构模型的子准则层，即指标层(C)。

根据上述因素分类，建立层次结构模型。本工程层次结构模型分为4 个层次(见图1)。

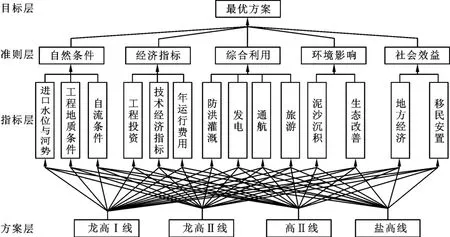
图1 渠线方案选择递阶层次结构模型图Fig.1 Model Diagram for hierarchical structure of selecting drainage line scheme

3.2 构造判断矩阵

判断矩阵是AHP 工作的出发点，AHP 的信息基础是人们对每一层次各因素的相对重要性给出的判断，这些判断用数值表示出来，写成矩阵形式就是判断矩阵。判断矩阵的量化由各因素之间进行两两比较确定，根据专家打分法，采取1～9 标度给出。

假定A 层中元素Ak 与下一层B1、B2、……、Bn 有联系，则构造的判断矩阵见表4 所示。

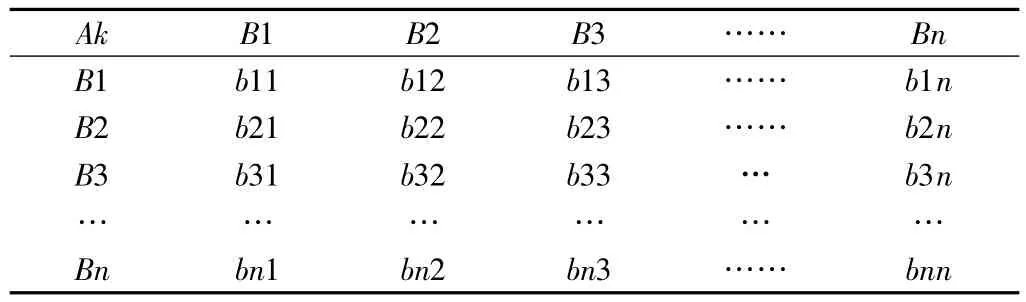
表4 判断矩阵的结构形式Table 4 The structure of judgment matrix

其中，bij 表示对于Ak 而言，Bi 对Bj 的相对重要性的数值表现，通常bij 可取1、2、……、9 及它们的倒数，其取值可通过专家咨询法来确定。显然，对于判断矩阵中的元素应满足:bii=1、bij=1/bji(i、j=1，2，……，n)。当判断矩阵中元素满足bij=bik/bjk(i、j、k=1，2，……，n)时，则称判断具有一致性。

目标层A 与准则层B 的判断矩阵见表5。

表5 A-B 判断矩阵Table 5 A-B judgment matrix

准则层B 与指标层C 的判断矩阵见表6～7。

表6 B-C 判断矩阵(BC1-BC3)Table 6 B-C judgment matrix(BC1-BC3)

表7 B-C 判断矩阵(BC4-BC5)Table 7 B-C judgment matrix(BC4-BC5)

指标层C 与方案层D 的判断矩阵见表8～12。

表8 C-D 判断矩阵(CD1-CD4)Table 8 C-D judgment matrix (CD1-CD4)

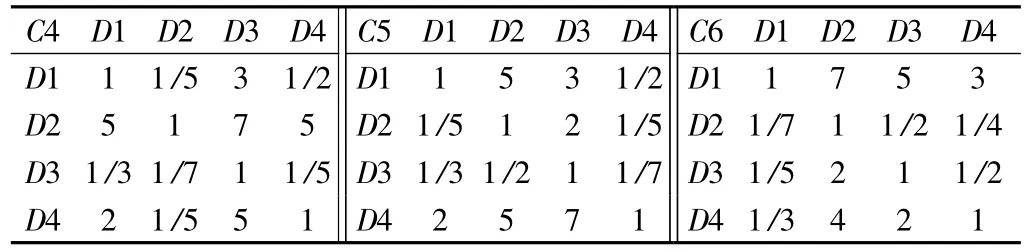
表9 C-D 判断矩阵(CD4-CD6)Table 9 C-D judgment matrix (CD4-CD6)

表10 C-D 判断矩阵(CD7-CD9)Table 10 C-D judgment matrix (CD7-CD9)

表11 C-D 判断矩阵(CD10-CD12)Table 11 C-D judgment matrix (CD10-CD12)

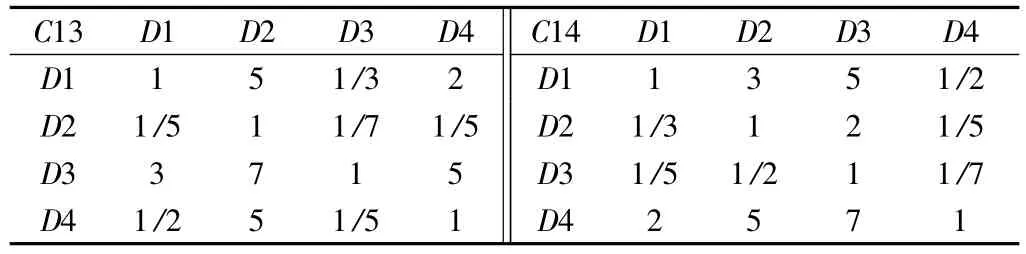
表12 C-D 判断矩阵(CD13-CD14)Table 12 C-D judgment matrix (CD13-CD14)

3.3 计算最大特征根及特征向量

依据层次分析法计算原理，需对各判断矩阵进行层次单排序及一致性检验。层次单排序是指根据判断矩阵计算对于上一层某元素而言，本层次与之有联系的元素相对重要性次序的权值。层次单排序要计算判断矩阵的最大特征值及其特征向量。记判断矩阵的最大特征根为λmax，与最大特征根相对应的特征向量记为W(向量W 要作归一化处理)，那么向量W 的分量wi则为相应元素排序的权值。一致性检验的目的是为了检验判断矩阵的构造是否合理，其检验指标CI 计算公式为:

式中:λmax——判断矩阵的最大特征值;n——判断矩阵的阶数。

判断矩阵是否具有满意的一致性，还需要利用判断矩阵的平均随机一致性指标。RI 的取值可通过查表给出。对于1～9 阶判断矩阵，其取值见表13。

表13 1～9 阶平均随机一致性指标RI 取值Table 13 The RI values of average random consistency indexes from 1 to 9 order

当判断矩阵的随机一致性比率CR=CI/RI ＜0.1时，则认为判断矩阵具有满意的一致性，否则需要调整判断矩阵。

通过计算，各判断矩阵的最大特征值及其特征向量如下:

(1)A-B 判断矩阵 λmax=5.227 6

WBA=［0.1174 0.4550 0.3019 0.0851 0.0406］

该判断矩阵的一致性指标CI=0.056 9，CR=0.050 8 ＜0.1，判断矩阵具有满意的一致性。

(2)B-C 判断矩阵 计算结果见表14。

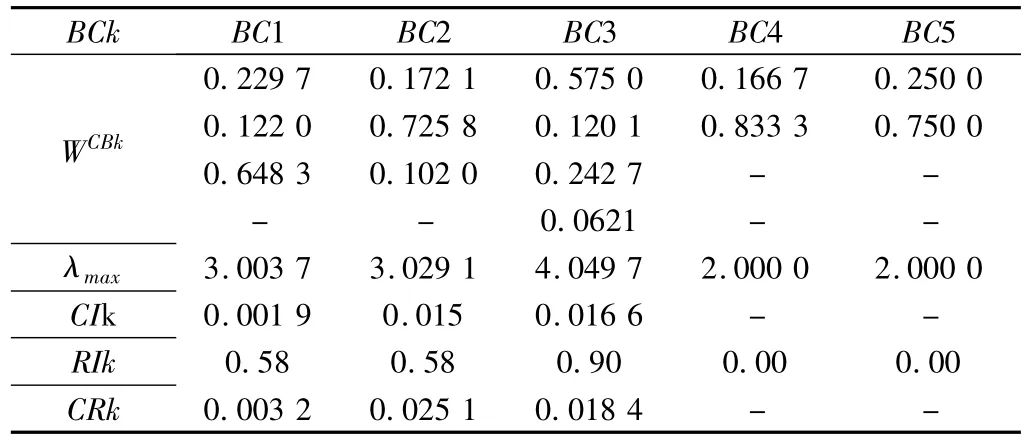
表14 B-C 判断矩阵的最大特征根和特征向量及一致性检验计算结果表Table 14 Results for the biggest characteristic roots，and characteristic vectors of B-C judgment matrix，and consistency test

判断矩阵中，CRk(k=1，2，3，4，5)均＜0.1，判断矩阵具有满意的一致性。

(3)C-D 判断矩阵 计算结果见表15。

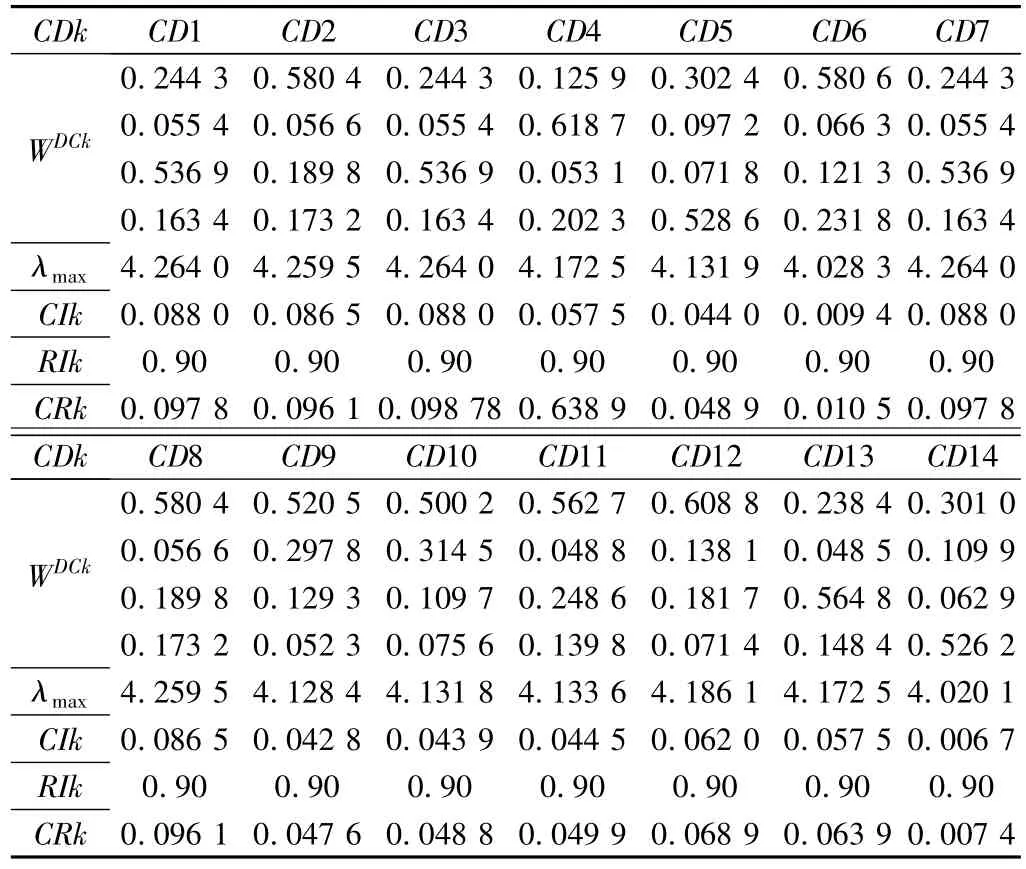
表15 C-D 判断矩阵的最大特征根和特征向量及一致性检验计算结果表Table 15 Results for the biggest characteristic roots，and characteristic vectors of C-D judgment matrix，and consistency test

判断矩阵中，CRk(k=1，2，3，……，14)均＜0.1，判断矩阵具有满意的一致性。

3.4 层次总排序及一致性检验

层次总排序实际上就是计算方案层中的各个方案对于目标层的权向量。利用同一层次中所有层次单排序的结果，就可以计算针对上一层次而言，本层次所有元素的相对重要性的权值，即层次总排序。层次总排序是从上到下逐层顺序进行，逐层合成的。

准则层(B)相对于目标层(A)的排序向量为WBA=［0.1174 0.4550 0.3019 0.0851 0.0406］，表示准则层相对于目标层的权重。

指标层(C)相对于目标层(A)的组合权向量计算为:

同样的，方案层(D)相对于目标层(A)的组合权重向量计算结果如下:

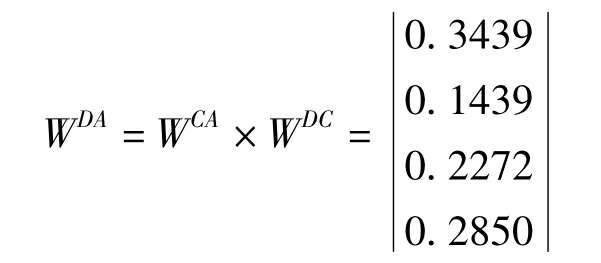
为评价层次总排序计算结果的一致性，也需要进行一致性检验。该检验计算自上而下逐层进行，其检验公式如下:

根据计算结果，层次总排序一致性检验指标CR ＜0.1，满足一致性检验。说明层次总排序的权向量是合理的。

根据层次分析结果，4 条比较渠线相对于最优方案的权重系数分别为:龙高Ⅰ线(D1 方案)为0.343 9，龙高Ⅱ线(D2 方案)为0.143 9，高Ⅱ线(D3 方案)为0.227 2，盐高线(D4 方案)为0.285 0。其总排序为:龙高Ⅰ线，盐高线，高Ⅱ线，龙高Ⅱ线，亦即龙高Ⅰ线为最优方案。

4 结语

层次分析法是一种将定性与定量相结合的多目标决策分析方法，特别是将决策者的经验判别定量化，较传统的定性分析方法更为科学合理，分析结果更加可靠。复杂的水利工程，特别是像南水北调这种特大型的跨流域调水工程，在决策过程中，影响因素众多，且相互关联、纷繁复杂，利用传统定性的方法处理起来难度大，且受人为主观因素的影响较大，难以得到客观、科学、合理的结果。层次分析法作为一种最优化决策方案，能有效地解决这类复杂的问题。

［1］张立中.层次分析法在水利水电规划中的应用［J］.华北水利水电学院学报，1987(1):49－56.

［2］刘家明，孙峥.引江济汉干渠渠线选择［J］.人民长江，2010，41(1):5－9.