法向承力锚安装过程的动力研究

冯 倩，孙克俐

(1.国核电力规划设计研究院，北京100095;2.天津大学港口海岸及近海工程系，天津300072)

法向承力锚(Vertically Loaded Anchor，VLA)属于新型拖曳嵌入锚.相比于传统拖曳嵌入锚，具有锚板面积大、工作时法向受力的特点［1］.安装时，由安装船提供的拖曳力通过卧底缆以水平方式施加到锚板上，驱使VLA深嵌.嵌入海床土过程中，锚爪在土抗力和拖曳力的共同作用下逐渐发生转动(如图1所示)，最终与海床面平行，达到极限嵌入深度.

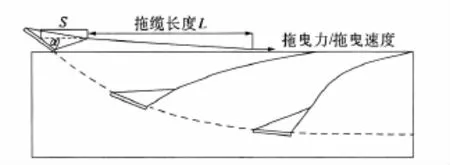
图1 法向承力锚嵌入轨迹示意图

VLA嵌入轨迹的研究方法包括实验研究、极限平衡法和塑性极限分析法.荷兰Vryhof公司分别在墨西哥湾和巴西近海对法向承力锚进行一系列小比尺实验［2］.1998年，Dahlberg和 Strom 联合挪威船级社在 Ons9y开展新型拖曳锚陆上模型试验［3－4］.英国Bruce公司在模型实验中采用半透明材料模拟海床土体，在玻璃槽中记录锚板的行进轨迹和形态变化，对定性研究VLA嵌入轨迹有重要的参考价值［5－6］.盛志刚等［7］建立了 VLA 模型试验系统.Neubecker和 Randolph［8］以及 Thorne［9］采用极限平衡法推导出了锚板的拖曳嵌入轨迹.O’Neill［10］采用塑性极限分析法对拖曳锚的运动轨迹进行了研究，所得出的结果同极限平衡法结果类似.目前国内针对VLA安装过程影响因素的研究较少.为此，笔者利用动力分析软件LS－DYNA建立VLA安装过程的动力模型，采用ALE算法处理法向承力锚与土体之间的相互作用，研究相关因素对VLA的嵌入轨迹和极限嵌入深度的影响，为相关模型试验提供参考和对比.

1 动力仿真模型

1.1 法向承力锚与土体耦合的ALE算法

ALE 算法的基本控制方程［11－12］有以下 3 个方程.

1)质量守恒方程:

式中:ρ为密度;v为物质速度;w为相对速度;w=v－u;u为网格速度.

2)动量守恒方程:

式中:bi为单位体积力;σij为 Cauchy应力，Cauchy应力可分解为偏应力张量sij和静水压力p;σij=sij+pδij，δij为克罗内克 δ符号.

3)能量守恒方程:

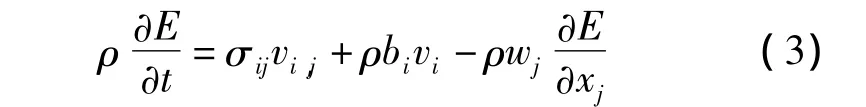
式中E为内能.

ALE有限元计算中，首先对土体网格执行一个Lagrange时间步，土体网格随材料流动而产生变形;保持变形后的土体模型边界条件，对土体模型内部网格进行重划分;将变形后的土体单元变量(密度、能量、应力张量等)和节点速度矢量输运到重分后的新网格中.ALE算法既可有效地追踪VLA系统边界的运动，同时可有效地对土体大变形进行模拟.

1.2 模型简化

权衡建模的复杂程度和各因素对嵌入轨迹的影响，需将模型进行简化处理.包括:略去定位尾缆;拖曳力直接施加在卧底缆上;略去法向承力锚的角度调节器;锚板形状简化为正方形.模型示意如图2所示.

图2 简化后的法向承力锚安装系统

1.3 模型材料及参数

1)锚板.材料为钢.嵌入过程中变形可以忽略，因此设置锚板为刚体，其尺寸参数见表1.

表1 锚板的尺寸参数

2)锚径及拖缆.材料为钢丝绳.模型中假定锚径及拖缆为弹性材料，具体参数见表2.

表2 锚径和拖缆材料参数

经试算，模型中拖缆长度L(如图1所示)＞30 m，继续增加长度对VLA极限嵌入深度的影响＜5%，故取拖缆长度为50 m.

3)海床土.假设:①海床土为符合Mises屈服准则的理想弹塑性材料;②土体不排水抗剪强度Su(kPa)在海床面处为零且随深度线形增大，即Su=1.5H;③土体弹性模量为不排水抗剪强度Su的500倍，泊松比为0.45，Mises屈服应力 σs为√3Su.

1.4 模型验证

建立验证模型与文献［3］中场地试验对比，结果见表3.

表3 验证模型与场地试验结果对比

由表3可得出:同一时刻场地试验的嵌入深度比验证模型嵌入值大9.6%左右.产生误差的原因有两方面:①锚板外形的差距.场地试验所采用的锚板为工程用锚板，外形经过优化设计.验证模型的锚板为长方形薄板，厚度为常数，略显笨重，因此会对嵌入深度产生一定影响.②场地试验之前，同一场地上已进行了类似试验，土体结构的变化会对嵌入深度产生影响.

由于文中侧重研究各因素变化对VLA嵌入轨迹的影响，VLA的实际嵌入深度不在此文讨论范围.因此未对锚板进行更精细模拟.

2 各要素对嵌入过程的影响

设计3组试验(见表4)，研究设计锚径角、拖曳速度对法向承力锚嵌入过程的影响.

表4 法向承力锚下嵌轨迹研究试验分组

2.1 拖曳速度对嵌入的影响

试验结果如下:嵌入轨迹对比如图3所示;卧底缆上拖曳力随时间变化对比如图4所示;下嵌2.5 m时拖曳力对比见表5.

由图3和图4可以得出结论:当拖曳船提供的拖曳力有限时，在一定范围内减小拖曳速度不会改变法向承力锚的下嵌轨迹.由表5可得出结论:拖曳速度增加到0.8 m/s之后，嵌入海床面以下2.5 m时所需拖曳力将逐渐趋于稳定.

图3 不同拖曳速度时的嵌入轨迹曲线

图4 不同拖曳速度时拖曳力的变化曲线

表5 下嵌2.5 m时拖曳力对比

2.2 设计锚径角对潜入的影响

实验结果如下:图5为轨迹对比图;图6为嵌入速度随时间变化对比图;图7为拖曳力随时间变化对比图;表6为嵌入特征值对比结果.

图5 不同设计锚径角时的嵌入轨迹曲线

图6 不同设计锚径角时嵌入速度的变化曲线

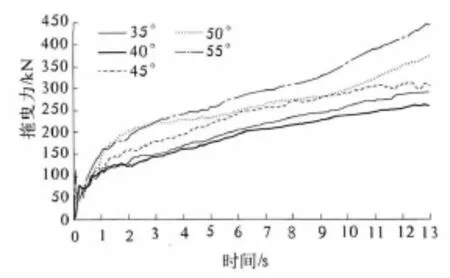
图7 不同设计锚径角时拖曳力的变化曲线

表6 不同设计锚径角对锚板嵌入深度的影响

数值分析表明:当设计锚径角为60°时，法向承力锚下嵌不久即被拔出海床面，不能成功完成安装.因此，根据本次试验的计算数据，设计锚径角的最大值不能超过60°，本模型给出的推荐值为45°～55°.

3 结语

1)采用ALE技术可成功进行法向承力锚嵌入海床土过程的数值仿真模拟.文中从这一数值分析模型中摘取部分研究成果进行撰写.以后还将继续进行深入研究.

2)拖曳速度不会改变法向承力锚的下嵌轨迹.拖曳速度增加到0.8 m/s之后，嵌入海床面以下2.5 m时所需拖曳力将逐渐趋于稳定.

3)设计锚径角最大不能超过60°，本模型给出的推荐值为45°～55°.

［1］刘海笑，杨晓亮.法向承力锚(VLA)——一种适用于深海工程的新型系泊基础［J］.海洋技术，2005，24(3):78－82.

［2］ Vryhof Anchors.Anchor Manual［M］.The Netherlands:Krimpen and Yssel，2005.

［3］ Dahlberg R，Strōm Peds.Unique onshore tests of deepwater drag-in plate anchors［C］∥Proc 31st Annual Offshore Technology Conference.Houston，Texas，1999:713 －724.

［4］ NCEL.Drag embedment anchors for navy moorings［C］∥Techdata Sheet 83-08R，Naval Civil Engineering Laboratory，Port Hueneme，California，1987.

［5］ American Petroleum Institute.Recommended practice for design and analysis of station keeping systems for floating structures［C］∥API-RP-2SK，Washington，1995.

［6］ DNV.Design and installation of drag-in plate anchors in clay［C］∥Recommended Practice RP-E302，Det Norske Veritas，2002.

［7］盛志刚，刘海笑.深海系泊法向承力锚模型试验系统［J］.海洋技术，2009，28(3):92 －96.

［8］ Neubecker S R，Randolph M F.Profile and frictional capacity of embedded anchor chain ［J］.Geotechnical Engineering:Eng Div，ASCE，1995，121(11):787 －803.

［9］ Thorne C P.Penetration and load capacity of marine drag anchors in soft clay［J］.Journal of Geotechnical and Geoenvironmental Engineering，ASCE，1998，124(10):945－953.

［10］ Bransby M F，O’Neill M P.Drag anchor fluke-soil interaction in clays［C］∥Proc Int Symp on Numerical Models in Geomechanics(NUMOG Ⅶ)，Graz，Austria，1999:489－494.

［11］ Belytschko T，Liu W K，Moran B.Nonlinear Finite Elements for Continua and Structure［M］.New York:John Wiley ＆ Sons Ltd，2000.

［12］ Liu W K，Belytschko T，Chang H.An arbitrary Lagrangian-Eulerian finite element method for path dependent materials［J］.Computer Method in Applied Mechanics and Engineering，1986，58(2):227 －245.