弧底梯形渠道收缩水深计算方法的简化

滕 凯，张丽伟

(1.齐齐哈尔市水务局，黑龙江齐齐哈尔161006;2.齐齐哈尔市河道管理处，黑龙江齐齐哈尔161006)

弧底梯形明渠具有水流条件好，受力性能优越，断面曲线平滑，便于渠面衬砌机械化施工、连续作业［1－6］等优点，因此，该种断面形式也越来越广泛地应用于水利水电供排水工程中［7－8］.由于弧底梯形明渠断面的水力计算涉及高次方程求解问题，常规的试算法、图解法［9］或是计算过程繁琐，或是求解成果精度不高，不便应用;若用计算机编程求解又不便于基层工程技术人员的实际工作［10－13］.因此，有关弧底梯形明渠断面正常水深及临界水深计算方法的研究开展较多［14－18］，无论是公式的表达形式，还是计算精度都取得了令人满意的结果.但截止目前，对于弧底梯形明渠收缩水深计算方法的研究，尚未发现相关成果.因此，研究便于实际工程应用的简化公式，对提高弧底梯形明渠断面收缩水深的设计工作效率及计算精度，具有一定的实际意义.

笔者通过对弧底梯形断面明渠收缩水深基本方程变形、整理后的超越函数进行优化拟合替代，得到了表达形式简单、计算过程简洁、求解精度高、使用范围广的简化近似计算式.

1 收缩水深的基本计算方程

据水力学原理［19］，收缩水深基本计算方程为

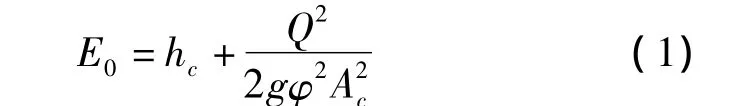
式中:E0为以收缩断面底部为基准面的过水建筑物上游总水头，m;hc为收缩断面处的水深，m;Q为过水流量，m3/s;g为重力加速度，通常取9.81 m/s2;φ为流速系数;Ac为与收缩水深hc相对应的抛物线形断面面积，m2.

弧底梯形过水断面图如图1所示.图中m为坡比系数;h为水深;b为水面宽度;r为弧底圆形半径.其收缩水深计算可分两种情况:弧底圆形断面收缩水深计算(圆弧内)和弧底梯形断面收缩水深计算(圆弧外).

图1 弧底梯形断面图

1.1 收缩水深计算公式判别

由弧底梯形断面过流条件可知，当收缩水深位于弧底曲线与梯形边坡线的切点以下时，收缩水深发生在圆弧内，反之，收缩水深发生在圆弧外.用数学方法可求得水面线通过切点处的收缩水深为

因此可得:

由式(2)可见，当m→∞时，hc→0，切点逐步接近弧底顶点，渠道断面渐进于一条直线;而当m→0时，hc→r，渠道断面逐步接近于U形明渠.

1.2 收缩水深发生在弧底圆弧内

当收缩水深发生在圆弧内时，收缩水深按圆形断面条件计算，其水力要素为:

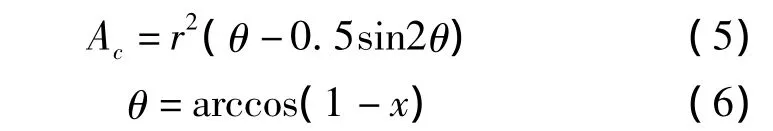
式中θ为与收缩水深hc相对应的圆心角的一半，rad.

将式(5)，(6)代入式(1)，并设

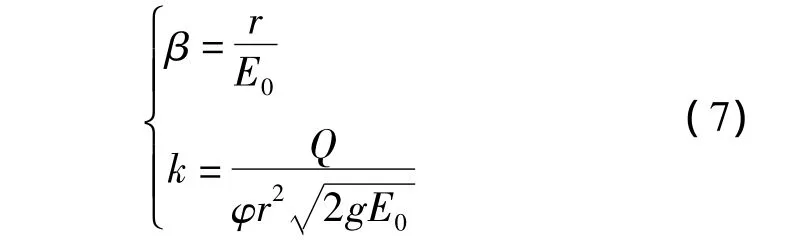
式中:k为无量纲已知综合参数;β为已知中间参数.

经进一步整理即可获得无量纲水深x的计算公式:

1.3 收缩水深发生在弧底圆弧外

收缩水深发生在圆弧外时，其过水断面水力要素为:

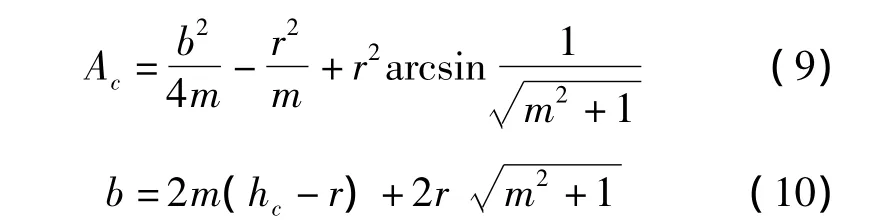
将式(9)，(10)代入式(1)，经整理即可求得无量纲水深x的计算公式，

2 收缩水深近似公式及精度分析

2.1 拟合公式的建立

式(8)及(11)为含x的超越或高次方程，无法直接获解.为此，笔者采用拟合替代的方法提出简化计算公式.

在式(8)及(11)中，设

在工程实用范围内，现假定:当收缩水深发生在弧底圆弧内及圆弧外时，函数y1=f(x)及y2=f(βx)可以分别替代式(12)中的y1及y2，并分别展绘y1－x及y2－βx关系曲线(限于篇幅，曲线图略)，依据曲线关系经数值回归分析，以最小标准剩余差为目标函数［20］，即

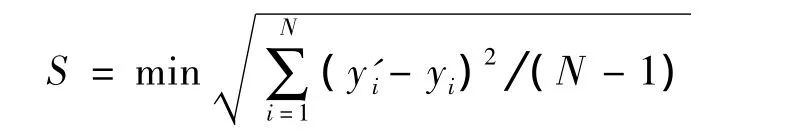
式中:N为拟合计算的数组数;yi为理论值;y'i为拟合计算值.

经逐次逼近拟合［21］即可获得如下替代函数，即

或

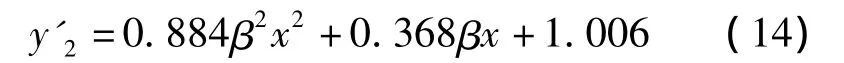
将式(13)，(14)分别代入式(8)及式(11)，经整理即可求得无量纲水深x.

当k＜k0时(收缩水深发生在圆弧内)，

当k≥k0时(收缩水深发生在圆弧外)，

式中:A，B，C，D均为中间变量;k0为收缩水面线通过弧底圆弧与梯形边坡切点情况下的渠道综合参数(界限参数)，可由式(1)，(2)，(5)，(6)联立求得:

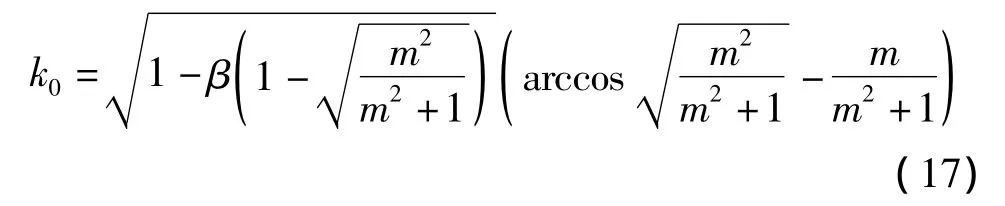
x求出后，即可用下式求得收缩水深hc，即

2.2 拟合公式的精度分析

为比较式(15)与式(8)、式(16)及式(11)的拟合精度，在给定的实用参数范围内，取不同的xi，βi及mi值分别由式(8)及式(11)计算出与之相对应的 ki，再将 ki，βi及 mi分别代入式(15)，(16)即可求得与之相对应的x'i(x'i为xi的拟合近似替代值)，并由式(18)计算拟合相对误差，进而根据各xi所对应的最大误差值(max(zi))绘制拟合相对误差包络线，如图2所示.

式中:zi为拟合相对误差;i为拟合计算的点数.

图2 拟合误差包络线

由图2 可知，当 0.1≤x＜1.0，0.01≤m≤7.00时，式(15)，(16)的拟合误差包络线在x轴的上、下摆动较大，最大正、负相对误差分别为0.727%和－0.741%，而当1.0≤x≤10.0 时，其最大拟合相对正、负误差的绝对值均不大于0.3%，且正、负误差的包络线为趋于平行于x轴的两条直线.可见，公式(15)，(16)具有较好的拟合精度，完全可以满足实际工程的设计精度要求.

3 应用举例

已知某引水渠道设计横断面为弧底梯形，弧底半径r=2.0 m，边坡比系数 m=3.0，进水口为一溢流坝，坝上设有闸控制，流速系数φ=0.95，试计算当闸前总水头 E0=10.0 m、引水流量 Q=100.0 m3/s和1.0 m3/s时渠道内的收缩水深 hc值.

1)当 Q=100.0 m3/s时，根据已知参数，由式(7)可求得:β =0.2，k=1.878 74.由式(17)可求得界限参数:k0=0.021 64＜k，因此选式(16)进行计算，因 λ =0.324 56，可求得中间变量:B=2.933 57，C=0.186 28，D= －1.892 82.从而求得无量纲水深x=0.772 14，则有:hc=1.544 3 m.

本例收缩水深的精确解为hc=1.547 1 m，文中公式计算结果的相对误差为－0.18%.

2)当Q=1.0 m3/s时，根据已知参数，由式(7)可求得:β =0.2，k=0.018 787.因 k ＜ k0，选式(15)计算无量纲水深 x.经计算可求得中间变量 A=3.704 07，则无量纲水深 x=0.046 33，由此得:hc=0.093 m.

本例收缩水深的精确解为hc=0.093 m，文中公式计算结果的相对误差为0%.

4 结语

针对目前弧底梯形断面收缩水深传统计算方法存在的问题，采用优化拟合的方法，对公式中超越方程进行拟合替代，获得了表达形式相对简单且具有较高拟合精度的近似计算公式.实际工作仅借助计算器即可完成解算，适合广大基层工程技术人员应用.应用实例的计算结果表明，文中公式计算方法简洁，结果精度可靠.

［1］杨彬.弧底梯形渠道全断面振捣连续滑膜衬砌机设计研究［J］.陕西水利，2010(6):91－92.

［2］王虎.不同断面形式防渗渠道的应用效果［J］.防渗技术，2002(3):31－33.

［3］李艳玲.弧底梯形混凝土衬砌渠道施工技术［J］.山西水利科技，2011(1):65－66.

［4］银俊梅.弧底梯形渠的冻胀试验研究［J］.中国农村水利水电，2001(12):140－143.

［5］王正中，李甲林，郭利霞，等.弧底梯形渠道衬砌冻胀破坏的力学模型研究［J］.农业工程学报，2008，24(1):26－31.

［6］宋玲，余书超.弧底梯形渠道受力特征及设计方法研究［J］.人民黄河，2010，32(8):128 －129.

［7］冯金祥，朱勤创.弧底梯形断面在宝鸡峡灌区应用的效益［J］.防渗技术，2001(2):33－35.

［8］王文龙.弧底梯形断面在夹马口灌区续改工程中的应用［J］.吉林工程技术学院学报，2004，20(3):56 －58.

［9］董为民，赵小利，刘卫华，等.底部含圆弧的梯形断面防渗渠道的水力计算［J］.水利与建筑工程学报，2005，3(3):54－57.

［10］杨茂松，马子普.一种弧底梯形明渠临界水深的快速解法［J］.吉林水利，2011(11):21 －22，23.

［11］赵晨.U形及弧底梯形渠道断面水力计算的搜索法与程序［J］.水利与建筑工程学报，2006，4(3):82 －84.

［12］孙铁蕾.EXCEL在常用明渠均匀流水力计算的应用［J］.水利规划与设计，2006(5):71 －72.

［13］成铁兵.弧底梯形及弧角梯形断面水力计算电算程序［J］.杨凌职业技术学院学报，2008，7(3):23 －25，29.

［14］李风玲，文辉，黄寿生.窄深式U形渠道正常水深的近似计算公式［J］.人民黄河，2006，28(12):75 －76.

［15］李风玲，文辉，陈雄.U形渠道水力计算的显式计算式［J］.水利水电科技进展，2010，30(1):65 －67.

［16］滕凯，邹伟，王洪波.圆底U形渠道均匀流水深计算方法的进一步简化［J］.灌溉排水，2001，20(1):74 －77.

［17］王正中，宋松柏，王世民.弧底梯形明渠正常水深的直接计算法［J］.长江科学院院报，1999，6(4):31 －34.

［18］王正中，申永康，彭元平，等.弧底梯形明渠临界水深的直接算法［J］.长江科学院院报，2005，22(3):6 －8.

［19］成都科学技术大学水力学教研室.水力学［M］.北京:人民教育出版社，1980.

［20］王慧文.偏最小二乘回归法及其应用［M］.北京:国防工业出版社，1999.

［21］阎凤文.测量数据处理方法［M］.北京:原子能出版社，1988.