基于特征结构分析法的静态电压稳定算法

钱俊良，李 鹏，陈巧玲，宋 喆

(华北水利水电学院，河南郑州450045)

电力系统电压稳定性从本质上讲属于非线性动力学系统的稳定问题，在数学上可以用一组非线性微分－代数方程组来描述［1］.静态电压稳定主要研究平衡点的稳定性问题，是目前电压稳定研究较多的方向之一［2］.其研究的主要内容包括:计算系统当前运行状态的电压稳定指标;确定系统的薄弱环节;寻找提高系统电压稳定的安全措施等.但是它要求系统受到扰动幅度足够小或者系统的变化过程足够慢以至于可以忽略系统模型的动态过程.

电压稳定静态分析法中最常用方法是特征结构分析法和快速解耦潮流法.这2种方法都直接或间接地利用了电力系统中存在的两大基本特征［3－4］:①当系统运行点接近静态稳定极限时，相对应的系统雅可比矩阵趋近奇异，此时与静态稳定极限状态相对应的雅可比矩阵的行列式值为零.②当系统运行点接近静态稳定边界时，相应的非线性代数方程即系统潮流方程存在且仅存在2个相邻的解;当运行点位于静态稳定边界时，则存在唯一解.笔者以特征结构分析法的2个基本特征为理论依据，准确地回答了电压不稳在何处发生，为什么会发生，哪些因素起关键作用等问题.

1 特征结构分析法的数学基础

在电力系统潮流计算中，假设系统有n个节点，其中第1至第m个节点为PQ节点，第n个节点为平衡节点，其余为PV节点.

极坐标系统下的潮流方程为

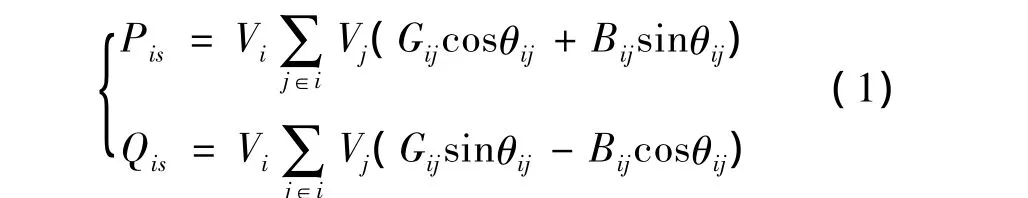
式中:Pis，Qis分别为给定节点有功和无功注入量;V，θ分别为给定节点电压向量和角度;Gij，Bij分别为导纳矩阵元素Yij的实部和虚部;j∈i表示∑号后节点j和i直接相连且包括j=i的情况.负荷采用ZIP模型，其电压静态特性为

将极坐标系统下的潮流方程进行摄动分析，得到线性关系式，

式中:

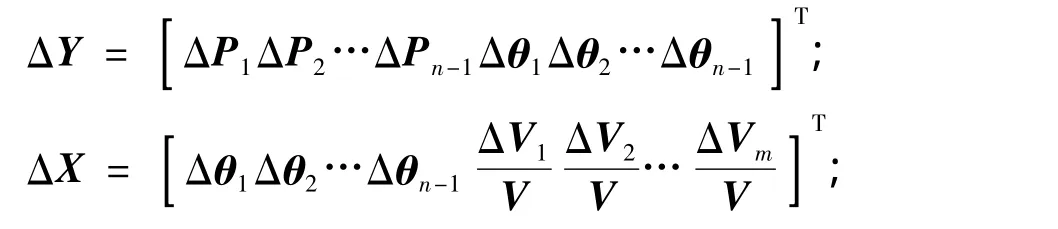
Jp为极坐标下的雅可比矩阵.ΔX，ΔY ∈ Rl×l，l=2n－m－1.

式(1)改写成矩阵形式

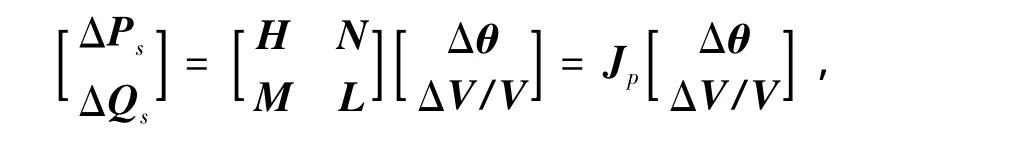
2 数学模型的建立

假设潮流方程中雅可比矩阵Jp具有非零相异特征根 λ1，λ2，…，λm，与之相对应的左、右特征向量分别为 V1，V2，…，Vm;U1，U2，…，Um.根据矩阵理论可知，矩阵行列式的值与特征根之间存在

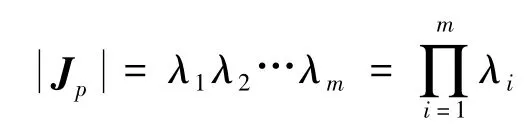
的关系.当系统达到静态稳定极限时，雅可比矩阵奇异.因此其存在一零特征根，当系统的运行状态由正常向极限过渡时，矩阵Jp有向奇异方向变化的趋势，与之相对应的最小模特征根首先单调趋近于零.因此可以作为系统静态稳定裕度判断的依据.

将式(2)中的ΔY，ΔX均用Jp的右特征向量基表示，即

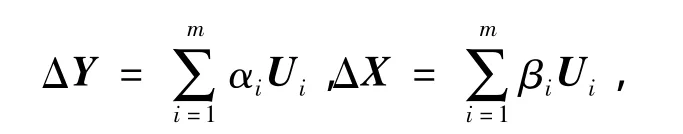
式中αi，βi分别为ΔY和ΔX与右特征向量Ui之间的耦合系数，并且满足 αi= βiλi，可求得

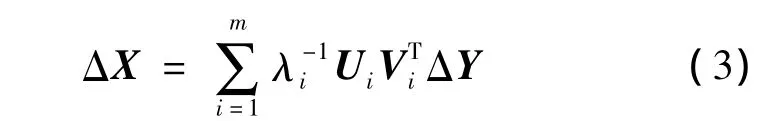
3 评价指标的建立

3.1 电压稳定裕度λmin的计算

由以上分析可知，系统稳定裕度的计算转化为雅可比矩阵最小模特征根的求取.就电力系统而言，无论是采用直角坐标系还是极坐标系，得到的雅可比矩阵都是非常稀疏的.因此可以先将雅可比矩阵通过初等相似变换为上赫申伯格矩阵，然后采用带原点位移的双重QR法求解全部特征根.这种方法具有强鲁棒性、收敛速度快等特点，是迄今为止最有效的特征根求解方法.

3.2 参与因子与节点电压灵敏度的计算

为了确定雅可比矩阵Jp与特征根之间的关系，把左特征向量和右特征向量结合起来形成如下所示的参与矩阵 P，用来衡量 Jp与特征根之间的关联度.

式中:Pki=ukivki为第k个状态变量对第i个特征根的参与因子;uki表示右特征向量ui的第k个元素;vki表示右特征向量vk的第k个元素.

用节点电压向量［Δθ ΔV］T代替 ΔX，用功率注入向量［ΔP ΔQ］T代替 ΔY，则式(3)转化为

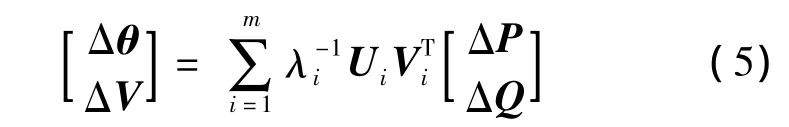
若取ΔP=0，ΔQ=ek，ek表示第k个元素为1，其余元素为0的单位列向量.假设系统有功注入量保持不变，仅在第k个节点上注入单位无功，则引起的系统状态变量变化为

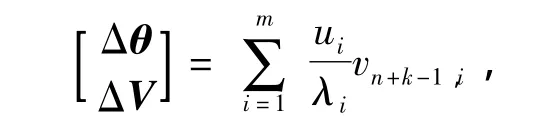
因此，第k个节点的电压灵敏度为

4 算例分析

以IEEE39节点系统为例在正常和极限两种运行状态下验证特征结构分析法的有效性.10台发电机分别置于30—39号节点，其中39号节点发电机为等值机.采用快速解耦潮流法求取其雅可比矩阵Jp，采用带原点位移的双重QR法求解全部特征根.

在参与因子与节点电压灵敏度的求取过程中，分别使IEEE39节点系统在正常和极限两种运行状态下求取部分负荷节点的功率，节点电压幅值，节点电压灵敏度dV/dQ及与最小模特征根λmin相对应的节点参与因子pki、计算结果见表1.表1中数据以正常运行时节点参与因子Pki从大到小顺序排列.

从表1可以得出正常运行时的总负荷为60.971+j14.089，λmin为 － 9.669;极限运行时的总负荷为71.942+j18.28，λmin为 0.正常运行状态所有特征根都具有负实部，表明系统运行稳定;极限运行状态下，出现了正实部和零特征根，表明系统电压已失去稳定性.

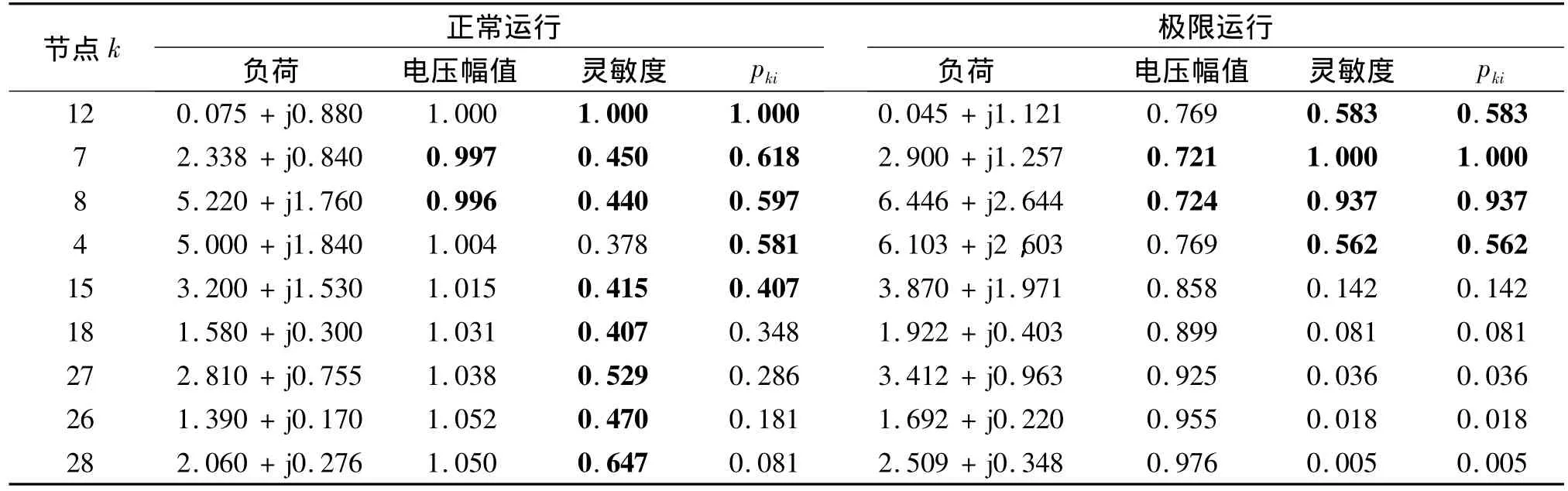
表1 IEEE39节点系统运行状态及其节点电压灵敏度

5 结 语

在系统正常运行状态下，即对应系统有较大电压静态稳定裕度时，节点参与因子pki与节点电压灵敏度dV/dQ在数值上有着较大差异.若将表中黑体数字所对应的节点构成此种运行方式下的电压薄弱区域，显然由dV/dQ灵敏度法确定的弱稳定区域是分散的，由节点参与因子pki值大小确定的弱稳定区域是集中的.

当系统处于极限运行状态时，对应的最小模特征根λmin=0，而且各个节点的相对电压灵敏度与该节点对应的相对参与因子数值完全相同，从而验证了电力系统总是以最小特征根所确定的模态(右特征向量)丧失电压稳定性，随着系统向着极限状态过渡，dV/dQ灵敏度趋向于 λmin对应的节点参数因子.

不同运行方式对应的节点参与因子及其电压薄弱区域一般来说都是不同的.由于本例中假设负荷均匀同比例增加，所以在正常和极限2种运行状态下所确定的电压薄弱区域基本相同，只是在极限运行状态下区域更小，更集中.从而也验证了电压失稳是从局部区域即节点7和节点8处首先开始发生.

［1］王锡凡，王万良，杜正春.现代电力系统分析［M］.北京:科学出版社，2003.

［2］吴际舜.电力系统静态安全分析［M］.上海:上海交通大学出版社，1985.

［3］周双喜，朱凌志，王小海，等.电力系统电压稳定性分析及其控制［M］.北京:中国电力出版社，2003.

［4］ Cutsem T V，Vournas C.电力系统电压稳定性［M］.王奔，译.北京:电子工业出版社，2008.