橡胶减振器数学建模
2013-08-28寇晓阳孟宪举
寇晓阳,孟宪举
(河北联合大学机械工程学院,河北唐山 063009)
0 引言
橡胶减振器作为一类重要的减振元件,已被广泛运用于各类机械、汽车、铁路机车、水上运输工具、飞机等领域。但橡胶在制作、加工、储存过程中,容易受到内外综合因素的影响而发生老化。温度太高,容易变黏;极易在矿物油中膨胀溶解;同时又不耐强酸。而且橡胶在受到很小的力时就会发生很大的形变,所以橡胶的弹性模量比较小,力学性能差,不适合单独作为减振材料。
本论文主要是对带有钢板叠层橡胶减振器进行研究,如图1所示,根据振动力学等相关理论对该系统建模,并通过实验验证数学模型的准确性。

图1 带有金属板的橡胶减振器
1 数学模型的建立
在一般环境下,橡胶能起到减振、缓冲的作用,但是在温度变化较大的环境下,橡胶的减振性能就变的相当不稳定,尤其是在高温条件下,由于橡胶的导热性能较差,致使橡胶变软,这时它的阻尼性能和力学性能都不稳定,承载力也会显著下降。所以在建模时我们首先假设橡胶的减振性能和承载力不随温度的变化而变化。
在力与位移的滞回曲线中,滞回曲线包围的面积就是在一个周期内粘性阻尼所消耗的能量。所以:ΔE=WC=ΠCB2ω 式中ΔE和WC就表示一个周期内阻尼力所消耗的能量,B表示振幅,C表示阻尼系数,表达式如下:C=
X是指整个系统的位移,X的表达式为:X(t)=Bsin(ωt)如果假设系统只受阻尼力,那么阻尼力Fd=,即:Fd==CBωcos(ωt);合并两式,可以得到如下表达式:
从表达式我们可以看出这个滞回曲线是一个标准的椭圆,如图2所示:
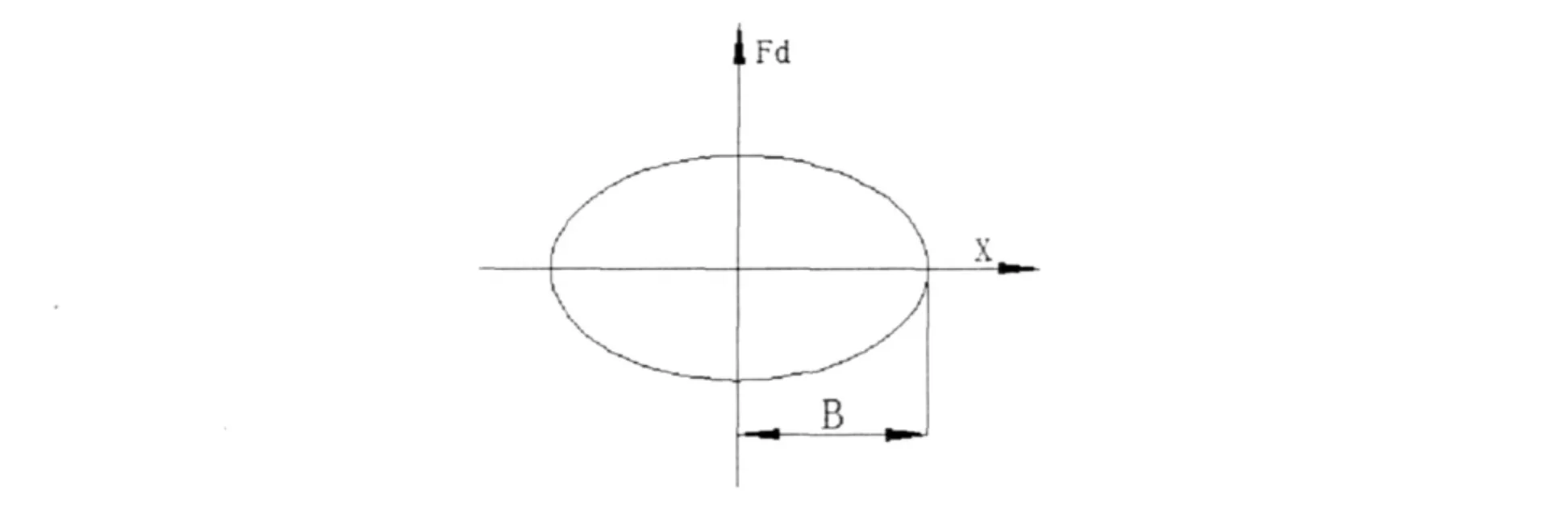
图2
但实际情况却不是这样的,我们通过实验得到的滞回曲线大致都如图3所示形状:

图3
这说明我们假设该系统只受黏性阻尼力是不正确的,还应该有弹性恢复力的作用,即KX,我们用FS来表示。
数学模型的建立主要依据Bingham模型来进行,但Bingham模型主要包括摩擦和粘滞单元;对于减振器来说,根据实验结果推断,我们还应加上弹簧单元。因而所建立的力学模型应该是Bingham模型与弹簧单元的组合。
把橡胶减振器作为抗冲击元件,其中起承载作用的主要是橡胶块,所以我们可以把橡胶块看成一个弹簧,它的刚度假设为k,减振器的阻尼系数设为C。
建立该单自由度系统的力学模型。如图4所示的力学模型,其中F为外界激励力,k、C分别是橡胶减振器的刚度和阻尼系数。

图4 力学模型
在加载过程中橡胶的变形大致可分为三个阶段,第一个阶段为屈服前阶段,也就是弹性阶段,当加载力使橡胶达到其变形极限时,此时是第二个阶段屈服阶段,最后一个是屈服后阶段。在实验过程中,减振器主要是在垂直方向运动,所以在建模的时候忽略了其他方向的振动,如果对该减振系统输入简谐振动,那么输出的响应和输入激励的频率应该相同,但由于阻尼的存在,输出的响应在振幅和相位上可能会发生改变。
假设输入减振系统的激励为:X(t)=Bsin(wt)
通过观察所建立的力学模型,可以得知橡胶阻尼器的回滞力F包括两部分,一是弹性力,二是粘性阻尼力,其数学表达式如下所示:
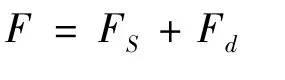
式中:FS为弹性力,其表达式为FS=KX;Fd为粘性阻尼力,表达式为Fd=。
所以F的表达式为:F=KBsin(ωt)+CBωcos(ωt)
2 减振器实验
2.1 实验综述
实验在HT-9711动态伺服试验台上进行。实验试件由4片橡胶板和4块金属板组成,如图1所示。安装在设备中的橡胶板试件会在设备的作用下发生剪切形变,实验设备自动将信号转变为剪切应力与应变、时间与位移图、位移与承载力的滞回曲线等三种曲线表现出来。通过多次实验选取形态最好的、最稳定的曲线进行分析。然后通过Matlab软件对曲线进行分析计算。
在测量试样截面尺寸并调整好仪器后,采用不同的加载频率和剪应变率对试件进行激励,取值如下表所示。

表1 加载频率

表2 剪应变
按照加载频率和幅值的组合,共进行21组试验,如1A、2A、3A、1B、2B、3B、……。
2.2 实验数据处理
在对实验数据进行处理时,得到如下三种曲线:
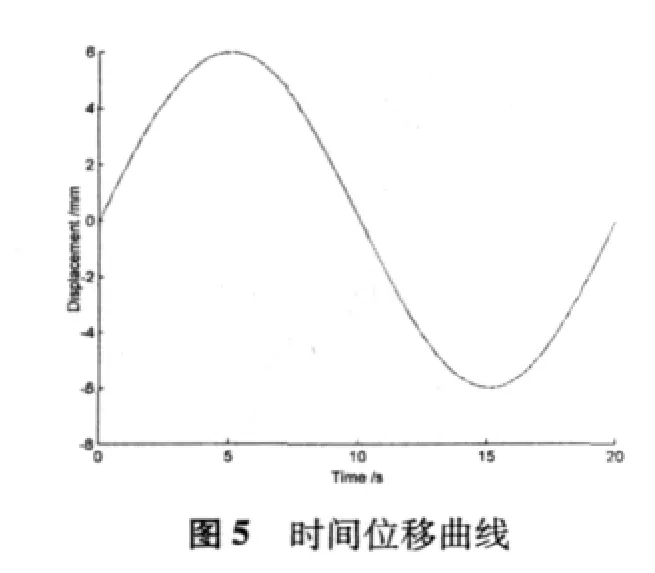
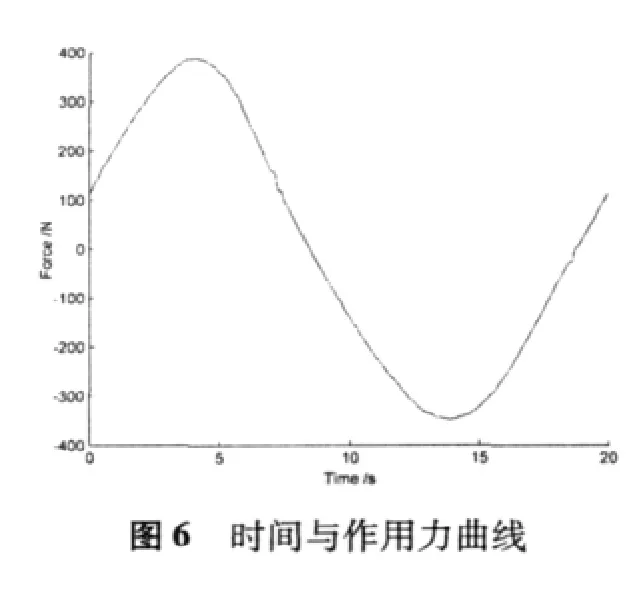

3 数学模型的验证
假设我们取B=0.3 mm,频率f=0.05 Hz,并用上述建立的力学模型来计算试件。用Matlab画出实验滞回曲线和理论滞回曲线。如图8所示:
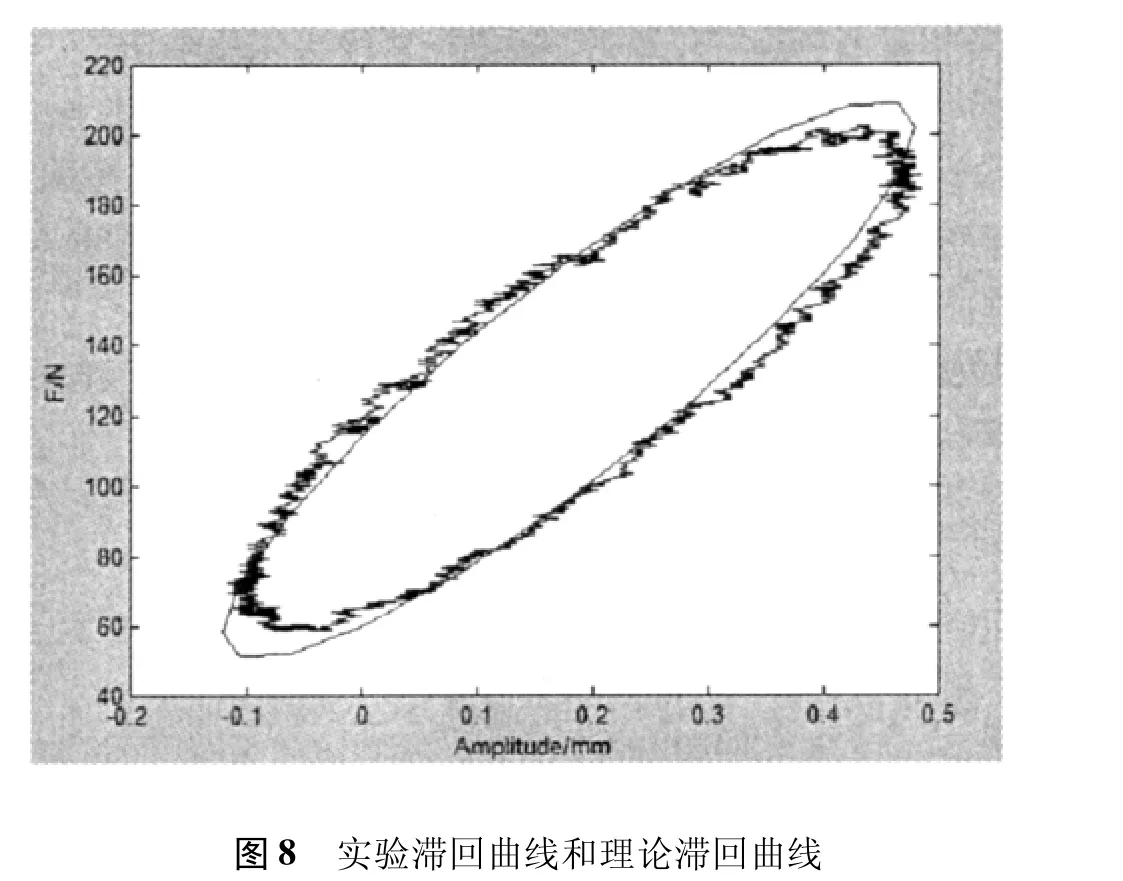
通过观察不难发现理论滞回曲线要比实验得到的曲线光滑,图形的形状基本吻合,但数值有些微小差别,这可能还包括一些其他力的作用,也可能是操作或者系统误差等原因造成的。
4 结论
(1)带有钢板叠层的橡胶减振器综合了摩擦阻尼器、粘滞阻尼器和弹簧阻尼器的性能,具有良好的使用效果。减振器的恢复力大体上可以分为两部分,粘性阻尼力和弹性力。
(2)通过对实验滞回曲线和理论滞回曲线进行对比,所建立的力学模型基本上可以描述橡胶减振器的基本特性。为工程实践提供了有力的理论依据。
[1]章绍辉.数学建模[M].北京:科学出版社,2010.
[2]陈泽,占海明.详解Matlab在科学计算中的应用[M].北京:电子工业出版社,2011.
[3]张义民.机械振动[M].北京:清华大学出版社,2007.
[4]胡振娴,顾亮.汽车减震器橡胶连接件动态特性实验研究[J].北京理工大学学报,2010(4):21.
