基于BP神经网络的CT图像重建方法研究

朱婷婷，李春芳

（中南民族大学 电子信息工程学院，湖北 武汉 430074）

1 引言

图像重建是光学CT技术的核心内容。在CT应用中，先是已知待测图像在几个方向上的投影，然后由这些投影数据重建出该图像。常用的算法主要有代数迭代法（ART）、滤波反投影（FBP）、最大熵法等。这些算法在投影数据比较多的情况下重建结果还比较理想，但在投影方向受限（如4～5个）的情况下，重建精度就很低[1，2]。

针对稀疏视角不完全投影图像重建的特点和难点，本文利用神经网络具有处理高维高度非线性和不确定问题的优势，提出了一种基于神经网络的图像重建方法。该方法充分利用神经网络具有强大的自适应学习和联想综合能力，故而可以实现所需的由已知投影值的视角区域到未知视角区域的弥补[3]，并且选用最简单的神经网络结构和有效的学习样本，从而在有限的条件下更有效地重建出高质量的图像。

2 基于BP神经网络的图像重建

2.1 BP网络模型及权值初始化

在各类神经网络中，BP神经网络是一种算法成熟且易于实现的网络类型。本文选用三层神经网络，即包含输入层、隐含层和输出层。

其中，输入层和输出层分别对应原始图像和重建图像的投影数据，神经元的个数为投影数据的个数。隐含层代表重建图像，神经元的个数为重建图像像素的个数[4]。在网络训练过程中，输入层至隐含层的权值W随误差的反向传播不断调整，隐含层至输出层的权值M在网络训练前事先初始化，并保持不变。根据CT图像重建理论，隐含层和输出层神经元之间的权值即为第i条投影射线穿过第j个像素的长度ri，j，故权值矩阵M即为投影系数矩阵R。笔者采用文献[5]新方法求取投影系数矩阵，从而确定权值矩阵M。

2.2 BP神经网络的改进

2.2.1 改进Sigmoid函数

在确定网络的训练数据和拓扑结构之后，总的误差函数E就由传递函数f给定，因此Sigmoid函数用于梯度学习，对于网络收敛具有十分重要的意义。实验表明：标准形式的Sigmoid函数不利于网络的收敛。为了解决这个问题，采用以下形式的Sigmoid函数[6]：

其中，β的作用是调节Sigmoid函数的形状。较大的β值使Sigmoid函数逼近线性阈值函数，而较小的β值将导致一个变化较为平坦的Sigmoid函数。在相同的初始条件下，通过调整β值，可寻求一个最佳形状的Sigmoid函数，使网络的学习次数达到最小。

经过多次选取不同的β值实验，发现当β取较大值（大于0.1）时，网络趋向于产生输出的分类，收敛效果很不好，重建图像误差很大；当β取较小值时，网络收敛效果较好，重建图像误差大大减小。通过对比选取不同β值的重建效果，本文最终选定β＝0.045。

2.2.2 在线调整学习速率

对于一个特定的问题，要选择适当的学习速率不是件容易的事情，通常是凭借经验或实验获取。况且，对训练初期效果好的学习速率，并不一定就对后来的训练合适，故最佳方法是能根据训练的需要自动调整学习速率的大小。即当误差降低时，可适当增大学习速率，加速网络收敛，如误差增大，说明产生了过调，就应当减小学习速率。下式给出了一种在线自适应调整学习速率的经验公式，其中，lr为学习速率，E为均方误差：

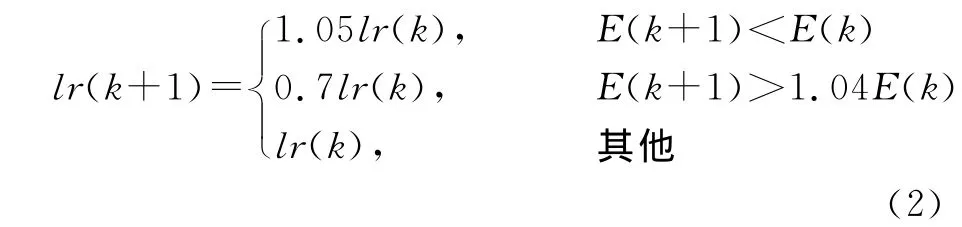
学习速率对收敛速度的影响很大，通过对它的在线调整，可以大大提高收敛速度。

2.3 网络学习过程

令ai为输入层第i个神经元的输出，Wji为神经元i与神经元j之间的连接权值，则隐含层神经元j的输出yj为：

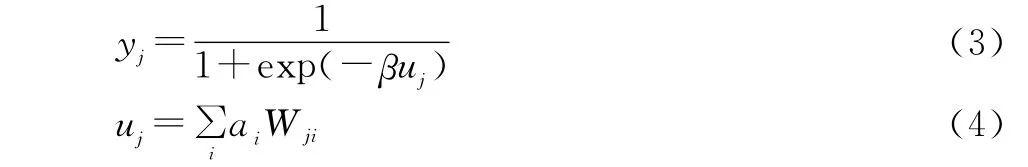
uj为隐含层第j个神经元的输入。则输出层第k个神经元的输出为：

BP算法的基本原理是采用梯度下降法使权值的改变总是朝着误差减小的方向，最终达到最小误差。则输入层与隐含层之间的权值修正公式为[7]：

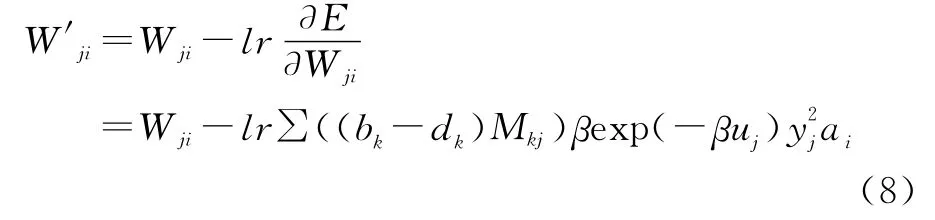
2.4 BP网络重建图像步骤

（1）初始化网络连接权值。计算投影系数矩阵R，确定隐含层和输出层之间的连接权值，并将输入层和隐含层之间的权值初始化为（0，1）之间的随机数。

（2）确定网络输入和输出。将原始图像在确定角度下的投影数据作为网络输入，网络输出数据和输入数据相同。

（3）计算隐含层输出。根据Sigmoid传递函数计算隐含层每个神经元的输出。

（4）计算输出层实际输出。根据已确定的权值计算输出层的实际输出。

（5）计算误差，调整权值。利用式（8）调整权值的大小。

（6）判断网络训练终止条件。当误差小于预设精度或学习次数达到设定的最大次数时，算法终止，否则返回第3步，进入下一轮学习。

3 实验结果及分析

本文选择Sheep－Logan模型并使用 Matlab7.8.0编程进行计算机模拟重建。待重建图像大小为20×20，采用5个角度方向上的投影（9°，45°，81°，117°，153°），分别利用改进前后的BP神经网络对模型进行重建，重建结果如图1所示。

通过仿真结果发现，传递函数对网络的收敛有很大的影响，通过在线调整学习速率虽然增加了网络的运算量，但仍能有效地加快网络收敛，提高收敛精度。如表1所示，其中，和eave和emax分别表示重建图像的平均误差和最大误差，t表示网络收敛时间。由图1可以看出，网络改进后，图像的重建精度有了很大提高。

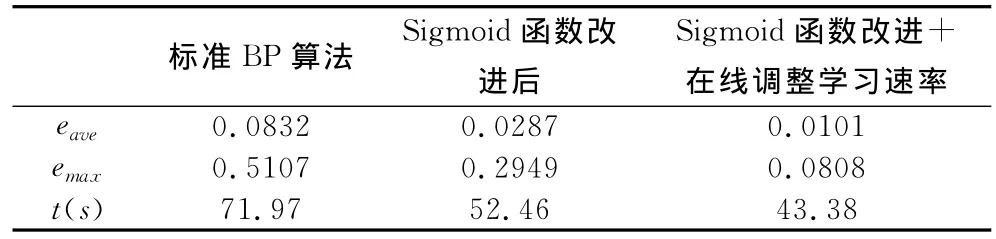
表1 不同情况下图像重建结果

图1 实验结果

4 结语

图像重建是光学CT技术的核心内容，重建图像质量和重建时间是图像重建的关键要素。本文利用BP神经网络实现了对不完全投影数据的图像重建，并通过对神经网络进行改进，显著缩短了重建时间，提高了重建精度。因此，本文提出的方法对于不完全投影数据重建提供了一个有效的解决方案。后续可以继续对重建图像做进一步处理，如进行分块重建、重建后加中值滤波等。另外，对BP神经网络的改进可以从不同的角度出发，本文只做了部分改进，今后的研究可以朝着进一步改进神经网络的方向进行。

[1]Nakao Z，Chen Yenwei，Kina Y.ART estimation of color images from projections[C].Joint Technical Conference on Circuits／Systems，Computers and Communications.Kumamoto，1995：217～220.

[2]孙毅刚，魏立新，张红颖.基于神经网络的CT图像重建方法研究[J].中国民航大学学报，2009，27（1）：1～3.

[3]Paschalis P，Giokaris N D，Karabarbounis A，et al.Tomographic image reconstruction using Artificial Neural Networks[J].Nuclear Instruments and Methods in Physics Research Section A，2004，527（1）：211～215.

[4]Ohkawa I，Nakao Z，Chen Yenwei，Tobaru S.Reconstruction of CT Images by the Back－Propagation Algorithm[C].Second International Conference on Knowledge－Based Intelligent Electronic Systems.Adelaide，Australia，1998：150～154.

[5]周 林，李春芳，陈方强.一种改进的光学CT扫描测量方法[J].计算机工程与应用，2008，44（28）：193～194.

[6]吴小培，费勤云.一种提高BP算法学习速度的有效途径[J].安徽大学学报：自然科学版，1998，22（3）：64～67.

[7]Nakao Z，Ali F E A F，Chen Yenwei.CT image reconstruction byback propagation[C].First International Conference on Knowledge－Based Intelligent Electronic Systems.Adelaide，Australia，1997.