采空区充填效果的随机规律研究

郭 力 何朋立

(洛阳理工学院土木工程系)

随着我国经济的迅速发展，对能源的需求不断增加，促使煤炭开采规模日益增大，易采资源日趋减少，对“三下一上”(建筑物下、铁路下、水体下和承压含水层上)压煤合理开采的意愿越来越强烈;同时，煤炭开采中还伴随着大量废弃物的排放以及塌陷区的出现，按传统的处理方式必然会对环境产生危害。而利用充填采煤技术，可较好地解决这两方面的问题。一方面因其对岩层扰动小，具有控制岩层移动与地表沉陷的作用，另一方面可以有效利用煤矿废弃物实施充填，减少废弃物的排放。因此，充填开采是煤矿绿色开采技术体系的主要内容之一，是解决煤矿开采环境问题和“三下一上”压煤开采问题的有效途径。

实际工程中，由于充填工艺、施工条件以及充填材料自身的特点等多个影响因素，不论何种充填方式，对采空区的充填都无法达到理想状态，其充填效果或程度不可能是绝对连续和均匀的。采空区充填效果的主要影响因素是充填材料和充填程度。此处充填程度是对充填方案中所要充填的采空区而言，也就是说，所要充填的采空区的理想或设计充填程度是100%，而实际操作中要达到这个程度几乎是不可能的。即使充填程度都是理想的100%，其充填材料也非完全连续和均匀的。显然，在实际中这是一个随机问题，其相关充填参数是随机变化的。由此，本研究借助随机有限元方法对此问题进行分析，以探究采空区充填效果随机变化情况下，围岩稳定性及地表沉降的统计规律。

1 计算模型

煤层埋深400 m，煤层厚度为3 m，不考虑煤层倾斜，即煤层水平分布。煤层直接顶为泥质粉砂岩，厚度为20 m。泥质粉砂岩之上至地面为表土层，表土层厚度为380 m。煤层直接底为中砂岩。计算时，模型上边界取至地面，模型下边界取煤层之下30 m，模型宽度取为600 m。则计算模型取矿区截面，总尺寸为(宽×高)600 m×433 m，采空区竖直尺寸为3 m，水平尺寸为600 m。采用平面应变模型，模型从上至下为表土层(厚380 m)、粉砂岩层(厚20 m)、煤层(厚3 m)、中砂岩层(厚30 m)。不考虑地表的附加荷载。

2 随机计算

2.1 方法选择

随机计算采用蒙特卡罗(Monte－Carlo)有限元法，该法通过在计算机上产生的样本函数来模拟系统的随机输入量的概率特征，并对于每个给定的样本点，对系统进行确定性的有限元分析，从而得到系统的随机响应的概率特征。蒙特卡罗有限元法是目前最常用的统计逼近法，可以获得输出随机变量与输入随机变量之间的关系。

2.2 随机输入变量

采空区充填效果的主要影响因素是充填材料和充填程度。不同的充填材料有着不同的力学特性，荷载作用下其表现有差异，因而对围岩稳定性及地表沉降有着不同的影响。充填程度直接影响到围岩和充填体的变形和受力。实际充填工程中，充填程度难以达到100%，但也不会存在太大的差距。因而当充填程度达不到100%时，采空区上部围岩存在一定的临空面。但这个临空面不会一直存在，随着变形的发展，上部围岩将会与充填体接触，充填体就会开始工作。

以上两个影响因素分别属于充填体的材料特性和几何尺寸，影响到充填体受载后的性能。由力学观点来看，二者均是改变了充填体刚度。本研究将充填体作为弹性体进行计算，由相关计算结果对比来看，影响弹性体刚度的主要是弹性模量。同时由于随机模拟计算需要大量的抽样，计算量比较大，而对弹性模量进行抽样计算不会对计算模型的几何建构产生影响，这在一定程度上降低了随机模拟计算的计算量，因而本研究将充填体的弹性模量作为随机输入变量。

对于随机输入变量，必须制定每个变量的分布函数类型。其中高斯分布是一个非常基本和常用的统计分布函数，一般用于描述许多物理现象的测量数据。而一般实际物理现象虽然服从高斯分布，但极限值是被限制的，或者要通过质量控制手段将样本所测数值规定在一个范围内。充填体的弹性模量也符合这一规律，选用截断高斯分布作为随机输入变量的分布函数。

由此，理想条件下充填体的弹性模量取为350 MPa，考虑到实际情况，将0.9×350=315 MPa作为随机输入变量的均值，变异系数取0.2(变异性中等)，则标准差为315×0.2=63 MPa，最小值为0.8×350=280 MPa，最大值350 MPa。

2.3 随机输出变量

对于采空区充填参数随机变化所带来的影响，从围岩稳定性及地表沉降两方面进行考量。当随机计算的循环次数达到一定数量，特征模型具有对称性。因此在计算模型中地表处取1点就可以代表地表沉降的变化规律。取模型中地表水平边界中点(对称轴处)的竖向位移作为一个随机输出变量，样本单位为cm，取名为UY。从采空区顶板和充填体两方面的受力情况来说明围岩稳定性，同理，本研究将模型宽度一半处(对称轴处)采空区顶板内1点的竖向位移、第一主应力以及等效应力

作为随机输出变量，样本单位分别为cm、MPa和MPa，分别取名为DB_UY、DB_S1和 DB_SEQV。同时，将模型宽度一半处充填体内1点的第一主应力和等效应力也作为随机输出变量，样本单位分别为MPa和MPa，分别取名为CTT_S1和CTT_SEQV。

由此，经过大量随机抽样计算后就可以得到以上这些随机输出变量的统计规律，从而可以分析采空区充填效果随机变化情况下，对围岩稳定性及地表沉降的影响规律。

3 采空区全充填

首先探讨煤层全开采、采空区进行全充填的情况。此时，若将充填体的弹性模量在整个模型宽度内保持一样的波动，这是不合理的。应将充填体划分为若干个区间，每个区间的充填效果是独立的，即将每个区间内的充填体弹性模量均作为随机输入变量，保持各自独立。若充填体划分的区间过多，随着随机输入变量抽样次数的增加，会使得整个模型的充填体弹性模量有均匀化的趋势，不存在明显的统计规律。因此，此处将充填体划分为10个区间，每个区间宽度是60 m。

计算进行500次循环。随着抽样次数的增加，均值和标准差是逐渐收敛的，且曲线趋向水平，说明循环次数和精度是足够的，样本数据是稳定的。直方图显示，样本数据接近概率函数分布，较为光滑，没有较大的间隙。图1给出了输出变量UY的均值和标准差的样本历史以及样本直方图，其余5个输出变量的均值和标准差的样本历史以及样本直方图在形态上与输出变量UY的较为接近，此处不再一一列出。

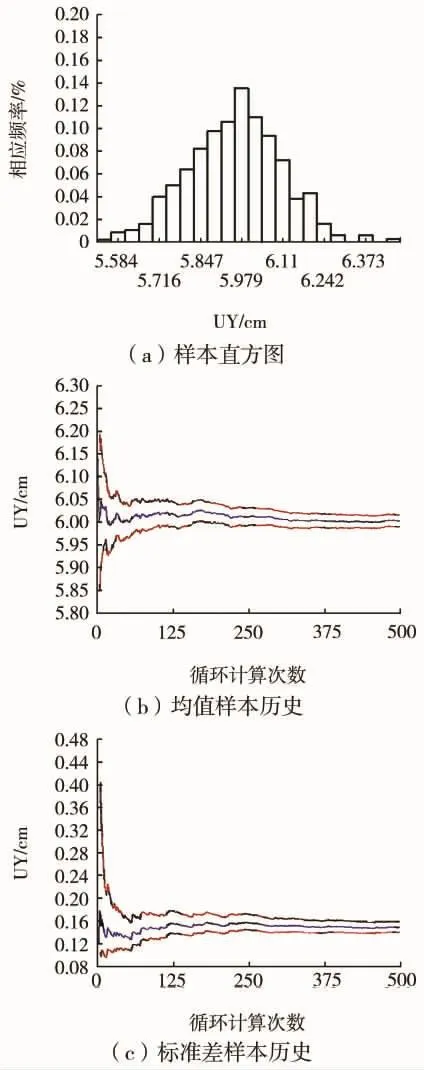
图1 输出变量样本直方图、均值和标准差样本历史

表1给出输出变量的样本均值、样本标准差、变异系数、最大值、最小值以及样本最大值与均值的比值。整体来讲，6个输出变量的变异系数都很小。相比较而言，地表沉降与采空区顶板沉降这2个竖向位移输出变量的变异系数比较大，其中采空区顶板沉降变异系数的数值最大。而其余与应力有关的输出变量的变异系数都比较小。这说明，在全充填的条件下，地表沉降与采空区顶板沉降对充填效果的变化比较敏感，其中与采空区相接的顶板最敏感。而充填效果的波动对应力有关的参数影响并不明显。这一点从样本最大值与均值的比值也可以看出。

表1 全充填时输出变量样本的相关参数

4 采空区部分充填

部分充填也是煤层全开采采空区常采用的充填方式。此时，同样将采空区划分为10个区间，每个区间宽度是60 m，其中40 m进行充填，20 m不充填。也就是每充填40 m范围的采空区，留出20 m范围不充填，之后继续进行充填。同样，每个区间内充填部分的充填效果视为独立的。

计算进行500次循环，样本的均值和标准差是逐渐收敛的，且曲线趋向水平，说明循环次数和精度是足够的，样本数据是稳定的。直方图显示，样本数据接近概率函数分布，较为光滑，没有较大的间隙，此处不再一一列出。

部分充填情况下的采空区中一定比例的范围是不充填的，对于随机问题来说，就是这部分采空区参数是固定的，不参与随机计算。与全部充填相比，部分充填的计算模型中随机变量所包含的范围和参与波动的范围减小了。

从表2给出的数据来看，整体上部分充填情况的各输出变量的变异系数均有较大的变化。同样，地表沉降与采空区顶板沉降这2个输出变量的变异系数比较大，其中采空区顶板沉降变异系数的数值最大。与之前全部充填的情况相比，此处地表沉降与采空区顶板沉降的样本均值都有较明显的增大，而二者的变异系数是减小的，但采空区顶板沉降的变异系数变化不大。由于存在一定厚度的表土层，采空区充填方式的改变，其充填效果的随机性对地表沉降的影响比较明显。

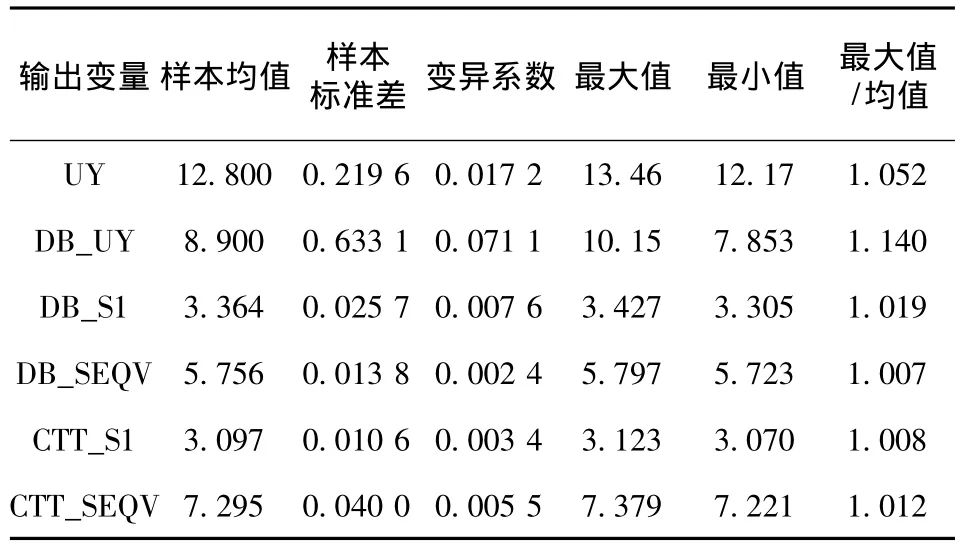
表2 部分充填时输出变量样本的相关参数

5 条带式开采

此处对煤层条带式开采出现的采空区进行全充填。采出条带宽度为40 m，保留条带宽度为20 m。如此，就相当于同样将采空区划分为10个区间，每个区间宽度是60 m，其中40 m进行充填，20 m保留为煤层。也就是采空区充填后，每40 m的充填体之间保留20 m为煤层。同样，每个区间内充填部分的充填效果视为独立的。

计算进行500次循环，样本的均值和标准差是逐渐收敛的，且曲线趋向水平，说明循环次数和精度是足够的，样本数据是稳定的。直方图显示，样本数据接近概率函数分布，较为光滑，没有较大的间隙，此处不再一一列出。

将此情况的计算模型中每个区间内保留的20 m宽度的煤层换为充填体材料，就与全充填情况的计算模型是一样的;将保留的煤层删除，就与部分充填情况的计算模型是一样的。从表3给出的数据来看，与之前的全充填与部分充填情况相比，由于保留了一定比例的煤层不开采，6个输出变量的样本均值均减小了，有利于围岩稳定性及地表沉降的控制。

表3 条带式开采时输出变量样本的相关参数

从地表沉降与采空区顶板沉降这2个输出变量的变异系数来看，条带式开采这种情况下的数值更接近于全开采部分充填的情况，这是由于相对于全充填情况，二者均存在部分采空区是固定的，不参与随机计算。

6 结语

(1)对比3种情况计算得到的样本均值，条带式开采由于保留了一定比例的煤层不开采，对于地表沉降的控制和围岩稳定性都是有利的。而对于煤层全开采，采空区全充填无疑是更理想的。

(2)根据本研究的计算模型与思路，且经过次数比较多的随机抽样计算，由输出变量的变异系数来看，6个输出变量对于采空区充填效果的波动并不敏感。相比较而言，地表沉降与采空区顶板变形对于充填效果的波动要更敏感一些。采空区的充填效果主要影响围岩的变形，进而影响地表的沉降，而对于围岩以及充填体自身受力的影响并不明显。

(3)多次抽样计算中各输出变量存在最大值与最小值，说明多个输入变量存在最不利组合与最有利组合。其中有的输出变量的最大值与均值的比值超过了1.1，应警惕最大值的出现。更科学的方法是采用一定置信度的置信区间来进行分析或设计。

(4)此外，同样的计算模型，减少抽样次数后输出变量的变异系数出现一定程度的增大。在相同的抽样次数下，将输入变量的抽样范围扩大后输出变量的变异系数出现较明显的增大，且二者并非线性关系。因此，应尽可能地保证采空区充填效果达到或满足设计要求，严格控制充填效果的变异程度以及变异范围，从而使充填方案要达到的目标具有良好的可控性或稳定性。

［1］ 许家林，轩大洋，朱卫兵.充填采煤技术现状与展望［J］.采矿技术，2011，11(3):24-30.

［2］ 邓 建，边 利，彭怀生.一种新的蒙特卡罗随机有限元方法［J］. 中南大学学报:自然科学版，2006，37(5):997-1001.

［3］ 陈 虬，刘先斌.随机有限元法及其工程应用［M］.成都:西南交通大学出版社，1993.

［4］ 李青锋，王 戈，朱川曲.长壁工作面充填开采的充填比与充填效益分析［J］. 矿业工程研究，2009，24(2):21-24.

［5］ 樊志强，赵玉成，王继燕.采空区充填前后岩层变形规律研究［J］. 煤炭工程，2011，(1):66-68.

［6］ 黄万朋，马树坤，朱全美，陈明程.井下采空区部分充填参数的确定［J］. 煤矿安全，2011，42(7):150-152.

［7］ 李海清，向 龙，陈寿根.房柱式采空区受力分析及稳定性评价体系的建立［J］. 煤矿安全，2011，42(3):138-142.