基于BP 神经网络的水泥混凝土施工质量控制

乔 亮 王承伟

(1.广州民航职业技术学院航空港管理学院，广东广州 510403;2.中国建筑业协会，北京 100081)

0 引言

随着机场设施建设规模的不断增大，机场建设中的工程质量问题变得越来越突出。为了保证工程质量，人们十分重视对工程质量的控制措施，且在不断探索改进工程质量管理的有效方法［1］，从而使机场工程的质量水平不断提高。

现有的质量预控方法较多，常见的有:统计学方法、模糊数学法等，虽然也能解决一些实际问题，但由于自身的缺陷，解决的问题难免有所局限［2］。在这种情况下，神经网络技术由于其独特的优点逐渐被人们应用到工程施工质量控制中。

1 BP神经网络理论

1.1 经典BP神经网络算法

误差反向前馈网络(Back-Propagation)是典型的前馈网络［3］，其算法的基本思想是:误差逆传播神经网络是一种具有三层或三层以上的阶层神经网络。典型的BP网络是三层，即:输入层、隐含层和输出层，各层之间实行全连接［4］。

1.2 经典BP算法缺陷

经典BP算法虽然具有广泛的实用性，但其由于自身缺陷存在以下几个问题:

1)容易陷入局部极小点，使算法不能收敛;

2)因反传修改权重使收敛速度异常缓慢;

3)隐层数和隐层节点数由于无成熟理论指导而难以确定;

4)学习、记忆性较差，添加新记忆模式时要重新训练。

1.3 本文算法的改进

针对于BP算法收敛速度慢的缺陷，本文采用对学习步长加入动量项的措施加以解决，动量项在每个权重的调节上加上一项正比于前一次权重的调节量的值为:

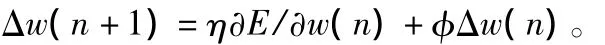
加入动量项后，使得权重的调节向着底部平均方向变化，即动量项起到缓冲与平缓的作用，这样就起到了调节网络的收敛速度。

隐节点数的多少对网络性能的影响较大，当隐节点数太多时，会导致网络学习时间过长，甚至不能收敛;而当隐节点数过小时，网络的容错能力差。利用逐步回归分析法，并进行参数的显著性检验来动态删除一些线性相关的隐节点。节点删除标准:当由该节点出发指向下一层节点的所有权值和阀值均落于死区(通常取±0.1，±0.05等区间)之中，则该节点可删除。最佳隐节点数P一般取:

其中，n为输入节点数;m为输出节点数;c为介于1～10的常数。

2 水泥混凝土质量预测模型的建立

2.1 水泥混凝土面层强度指标分析

影响混凝土强度的因素包括水泥的强度等级，水灰比，水的用量，水泥用量，粗集料的最大尺寸，骨料体积率，粗集料压碎值，粗集料中针片状颗粒含量，砂的细度模数，砂率，集灰比(集料与水泥的重量之比)，坍落度，外加剂的用量，外加剂的作用效果，成型条件，养护条件和测试条件等。其中的成型、养护和测试条件等3个因素在标准养护下，须符合规范要求，可视为不变的量。于是其余的14个因素在混凝土强度的形成中起决定性作用。这些因素和混凝土强度之间存在着复杂的非线性关系，利用BP网络构建预测模型，就是以14个影响因素分别对应BP网络输入层的14个节点，网络的输出层则有2个节点，即混凝土28 d的抗折强度和抗压标准值。

2.2 指标体系的优化

对于一个质量预控体系来说，初选指标的优化是一个重要的步骤。选择一个合理的优化方法，能有效解决训练速度过慢及训练过饱和等问题。

本文采用主成分分析法，将样本输入数据进行主成分变换，并通过主成分累计贡献率预设的临界值，确定前k个主成分，达到优化目的，可以作为下一步神经网络模型的训练样本。

2.3 输入数据预处理

由于在网络训练和仿真中使用的传递函数Sigmoid函数，它对输入、输出数据的范围有一定的限制:要求输入到神经网络的数据不能过大或过小，要求输出数据以［0，1］之间的数据形式表示，所以要对数据进行标准化或归一化处理。

本文将采用除以10的整数倍归一化方法，由于每个指标有不同的量级，用10的整数倍除以各指标数据，使其范围在0～1之间，达到标准化的目的并避免了约数的产生:

2.4 网络参数的选取

本文隐含层选取的激活功能函数为Log-Sigmoid函数，输出层功能函数为Liner函数;算法选用Resilient Backpropagation算法;性能调节函数选取msereg函数;学习函数选取Learngdm函数。n

2.5 网络的训练

已建立的神经网络模型必须经过训练才能应用于道面混凝土强度的预测中，训练的目的就是通过已有的工程施工数据输入神经网络反复迭代，让神经网络自己学习输入和输出的学习规则，最终建立所需的映射关系。

在此，人工神经网络的学习采用改进的BP算法，通过改进的BP算法对人工神经网络权值的优化来训练网络。

当达到预先设定的误差或训练次数时，训练会自动停止，赋予各指标权重合适的权值。

2.6 强度预测

训练好模型以后，将新的混凝土强度的特征信息经预处理以后输入到网络，得到的结果即是预测强度。

3 应用实例分析

3.1 选择应用数据

选择某高等级公路16个有关指标的33组数据(略)作为用于网络的训练，与此同时，使用天津机场扩建工程第二跑道道面施工中所做配合比试验中的数据，用来对训练好的网络模型作验证(略)。

3.2 输入数据优化分析

将上述所有数据合并，在MATLAB上将上述数据存入一个38-by-14阶的矩阵cement。执行命令:

计算结果发现，第14个指标标准差为0，对混凝土强度没有任何影响，故删除之。余下的13个指标存入矩阵cement1。

将矩阵cement1中对应的每列向量(对应每个指标的输入数据)，除以相应的标准差。这主要避免由于量纲的不同，造成的分析差异。可通过执行命令:

对变换后的数据矩阵sr进行主成分分析。可在MATLAB上执行如下命令:

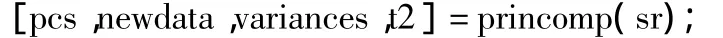
在这里，方差贡献率的大小表示相对应的主成分对混凝土强度的反映能力。由优化后的结果可知，后面一些主成分对混凝土强度的反映程度较小，我们选择累计方差贡献率达到95%为临界点，则选取前7个主成分为BP网络的输入，即可基本刻画相应的输出结果。

3.3 输出数据标准化

由选取的数据可知，混凝土抗压强度数值范围为10～50之间，抗折强度为3～6之间，计抗压强度为，抗折强度为33)，对输出数据进行“压缩”和作为网络训练和学习的样本。

3.4 模型训练

经上述分析可知，确定模型最终输入节点为7，输出节点为2，隐含层节点由公式(1)计算为12。

在MATLAB工具箱中输入训练数据，并且输入参数对网络进行训练，经过3 000次的训练以后，误差曲线已经平稳，说明网络模型全局误差已经收敛，网络训练结束后，可以进行下一步的预测。

3.5 模型验证

将表1中的数据输入到训练好了的网络中，就可得到预测混凝土强度值，预测值与实测值对照见表1。

表1 实测和预测强度对照表 MPa

由表1可以看出，预测结果能较好的反映出混凝土28 d的强度，抗折强度的增长与抗压强度的增长正比关系不明确，说明影响二者强度的主要因素不完全相同。所以在实际施工中，我们不能仅通过一种强度的明显提高，来实现另一种强度的显著提高。只有通过合理的材料配合，才能使两者同时达到令人满意的结果。

4 结语

混凝土道面作为飞行区最为重要的设施之一，其工程质量影响着飞机起降和滑行安全，通过应用改进的BP神经网络模型，可以对施工工序和施工方案进行预先评价和检验，在施工前就能消除各种不利因素，指导技术和施工人员按照合理的施工工序和施工方案进行施工［5］，以提高效率。在今后实践中，可不断的调整、完善模型，使预测结果更加符合实际情况。

［1］戚振强.建设工程项目质量管理［M］.北京:机械工业出版社，2004.

［2］George J，Ritz.Total Construction Project Management［J］.Mc Graw-Hill，Inc，1994(5):15-17.

［3］焦李成.神经网络系统理论［M］.西安:西安电子科技大学出版社，1990.

［4］王要武.人工神经网络在建筑管理中的应用［J］.哈尔滨建筑大学学报，2001，34(5):103-107.

［5］LarS，Serra M.Concrete Strength Prediction by Means of Neural Network［J］.Construction and Building Materials，1997(11):98.