下承式钢管混凝土拱桥抗震性能振动台试验分析

2013-08-23郭月哲

山西建筑 2013年14期

郭月哲

(山西省交通科学研究院，山西太原 030006)

0 引言

钢管混凝土拱桥自20世纪90年代引入我国。其以结构受力合理、跨越能力强、外型轻盈等特点正逐渐成为大中跨桥梁设计中有竞争力的桥型。钢管混凝土拱桥结构形式多样、拱肋样式富于变化，因此其动力特性具有自身特点;目前对钢管混凝土拱桥还没有建立起有针对性的抗震设计规范，且该桥型尚未经历大震的考验，对其抗震性能的掌握大多通过数值模拟分析。振动台试验是了解结构抗震性能的有效手段，介于以上可见有必要通过试验研究掌握钢管混凝土拱桥的动力特性及抗震性能。

本文以某下承式钢管混凝土拱桥为原型，通过刚度转换制作了单一材料的试验模型，实施了以研究其抗震性能的振动台试验［1］。通过整理分析，掌握了该桥型受不同地震波、在不同烈度等级作用下地震响应的特点及规律，得出了一些有益的结论。

1 模型振动台试验

1.1 试验原型及振动台简介

本次试验原型为某下承式钢管混凝土系杆拱桥。该桥主跨跨径99 m，矢跨比1/5，拱肋线形为二次抛物线。拱肋为哑铃形截面，采用双肢φ800 mm钢管加中部间距500 mm的钢板一对构成，管壁钢板12 mm厚，内填C40混凝土。拱脚处拱肋下部加劲为矩形断面。肋间设一字撑四道，截面为φ600 mm空心钢管。拱脚间用钢绞线作为预应力系杆，以承担恒载作用下的拱脚水平推力。每肋下的系杆为12根，每根为9束φ15.2 mm(7φj5)的钢绞线。吊杆为110φ5高强低松弛钢丝。吊杆横梁为钢筋混凝土工字梁。吊杆间距6 m。为加强桥面系的整体性，在系杆处设加劲纵梁。桥面板为预制钢筋混凝土板，湿接缝联结。桥面铺装为10 cm厚的C30防水钢筋混凝土。振动台试验在单向电液伺服振动台上完成。该振动台台面尺寸为2 m×2.2 m，最大载荷4.5 t，最大加速度1.0g，最大速度100 cm/s，可输入规则波和不规则波，有效频率范围为 0.5 Hz～20 Hz。

1.2 模型设计

为了更详实反映结构的动力特性及地震响应特点，试验模型几何相似比例取1/30。考虑到在试验室该相似比例下试验模型加工的难易程度及研究掌握结构整体抗震性能的试验目的等原因，本试验按照截面换算法，通过刚度相似关系，将原型拱肋钢管混凝土截面转化为纯钢截面再予以缩尺。截面刚度转换公式为:

其中，Ea，Eg，E分别为钢管混凝土中混凝土、钢管的弹性模量与换算截面的材料弹性模量;Aa，Ag，A分别为钢管混凝土中混凝土、钢管的截面面积与换算截面的截面面积;Ia，Ig，I分别为钢管混凝土中混凝土截面、钢管截面在组合截面中的截面惯性矩与换算截面的组合截面惯性矩;γa，γg，γ分别为钢管混凝土中混凝土、钢管的剪切模量与换算截面的材料剪切模量。

以式(1)，式(2)为主要计算依据;式(3)为参考。

缩尺后纯钢试验模型跨径3.3m，矢高0.66m，拱肋仍保持二次抛物线线形。其中构件截面具体尺寸如图1所示。试验模型在机械构件加工厂完成，细部尺寸误差控制在5 mm以内。

图1 模型各细部截面尺寸

由于振动台最大荷载限制，试验模型实际配重4 t，处于配重不足状态。根据相似理论及桥梁动力试验相关理论，欠配重模型试验各相似关系见表1。

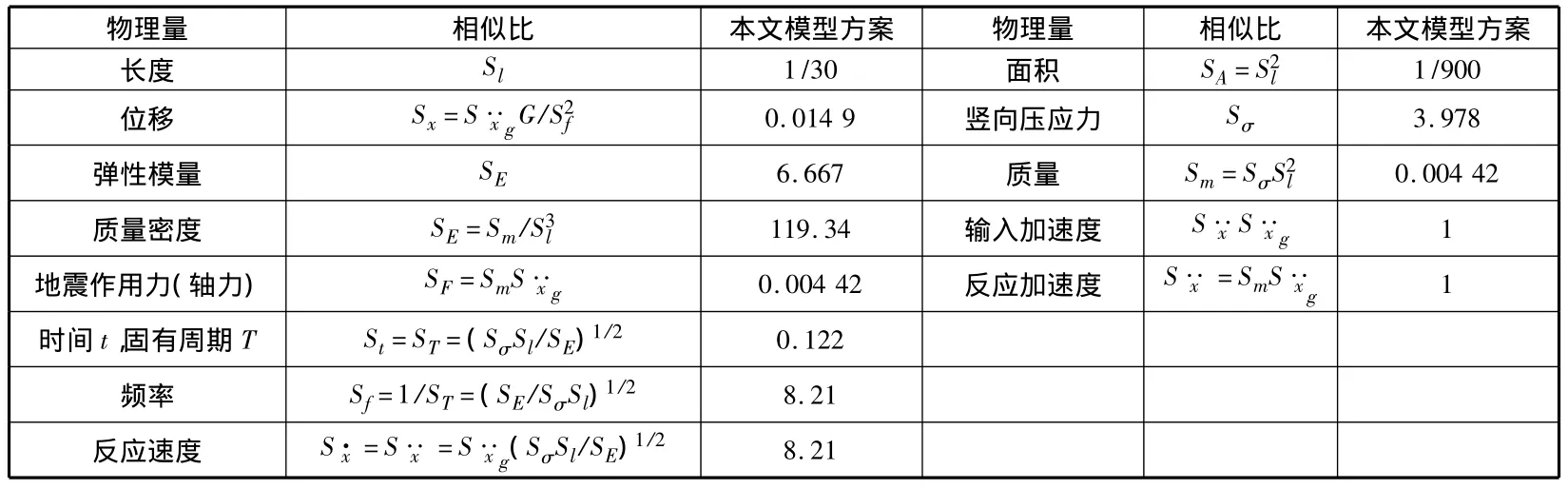
表1 模型相似关系

1.3 模型的安装

拱桥模型安装示意图见图2a)。试验制作辅助支座一对，模型一端通过固定支座与振动台台面螺栓刚性连接;另一端架设于滑动支座上，放于台面外。试验用滑动支座见图2b)。

图2 模型安装

1.4 加载方案与测点布置

1)模型加载。试验模型配重总计4 t，为了贴近原型实际工况，按照原型上部构件(拱肋和横撑)质量与下部构件(横梁、纵梁等)质量的比值进行分配。其中试验模型上部配重2.5 t，下部配重1.5 t。分部位配重情况见图3。

图3 模型加载步骤

2)输入地震波选取。试验中为了掌握释放能量方式不同的地震波作用下可能的结构响应的区别，输入地震波选取了释放能量集中的EICentro波或较均匀的Taft波作为输入波形。经过相似关系处理后，试验加速度控制在6度基本60 gal，7度基本120 gal，8度基本240 gal。其中EICentro波持时5 s;Taft波持时9 s。围绕基本烈度，同时试验加载工况中在区分烈度等级上还做了多遇、基本、罕遇、重要结构罕遇等工况。

3)传感器测点布置。本次拱桥模型振动台试验量测内容包括:加速度监测、位移量测和应变量测。其中加速度监测通过在振动台台面及滑动支座端设置加速度计，监测输入地震波波形及峰值大小，图4为试验监测的8度基本工况下的EICentro波和Taft波，波形完整。

图4 试验输入波形

位移量测是通过在试验模型各显著截面布设纵向和属相位移计，量测台面和拱肋各显著截面的位移变形时程，见图5。

为了掌握模拟地震波输入过程中拱肋内力的变化规律，分别在拱脚、拱肋1/4跨和拱顶等拱肋截面侧面沿轴向粘贴应变片，量测拱肋轴向应变。

2 试验结果分析

2.1 结构振动特性分析

振动台试验开始前对结构进行了锤击试验，测定模型拱肋面外及纵桥向自振频率，见表2。表2中附加了有限元计算结构前两阶振型:拱肋面外侧弯及拱肋和桥面板对称竖弯对应的振动频率。试验数据显示结构侧向自振频率明显小于纵向振动频率，符合通常对下承式钢管混凝土拱桥结构轻盈，侧向刚度小的直观判断。

表2 结构振动频率对比 Hz

2.2 拱肋应变响应分析

构件表面准确应变的变化能够很好描述其表面应力的变化趋势。试验中试通过量测拱肋表面轴向应变来掌握和分析拱肋应力的变化规律。如表3所示EI波和Taft波作用下，6度，7度，8度基本烈度工况下拱肋各显著截面的应变最值。同一地震烈度下，拱脚到拱顶的应变最值呈递减关系，约为拱顶应变的6倍～8倍。反映出拱顶应力较小，拱脚轴向应力起设计控制作用。

如图6所示EI波8度烈度下拱肋拱脚、1/4跨、拱顶应变时程曲线。拱肋内力显著截面的应变时程曲线波形接近地震波输入波形。