短期负荷综合预测模型新算法
2013-08-23朱玉华张坚锋
朱玉华,杨 扬,张坚锋
(1.中国石油大学胜利学院山东东营 257097;
2.中国石化集团胜利石油管理局测井公司,山东东营 257096)
0 引言
短期负荷预测是电力系统运行调度中一项非常重要的内容,其预测的准确度会对发供电企业的经济效益产生影响。一方面,由于预测负荷不足而导致的用电紧张和系统运行安全性下降将使机组承担更多负荷从而增加发电成本;另一方面,预测值过大,可能增加旋转备用的负担,造成运行费用的浪费[1-2]。因此,短期负荷预测是保证电网安全、经济和可靠运行的基础,是实现电力系统现代化管理的重要内容之一。
目前,负荷预测技术在处理数据、样本训练和回归分析的过程中,已经无法满足如今电力系统的飞速发展对负荷预测速度及精度的要求,因此,研究快速高效的负荷预测新技术很有必要[3]。
文献[4]提出了一种采用联合灰色模型 GM(grey model)和最小二乘支持向量 LS2VR(least square support vector regression)算法的电力短期负荷组合预测方法。该方法通过对历史负荷数据的不同取舍,构建不同的历史负荷数据系列,对每个历史序列分别建立GM(1,1)灰色模型进行预测,再通过最小二乘支持向量回归算法对不同灰色模型的预测结果进行非线性组合,从而获得最终预测值。
伴随着电力改革,越来愈多影响负荷发展的不确定因素导致负荷预测精度降低,使用单一预测方法已经不能满足电力负荷预测的需要,随之产生更为新型的预测方法—综合预测。它的主要原理是将不同的单一预测方法进行组合,或者将预测结果以不同权重加以组合。综合预测的精度一方面依赖于综合预测模型,另一方面还对单个预测模型要求较高,因此提高单项模型的预测精度是提高综合预测模型精度的前提。
1 负荷数据分析及预处理
1.1 理论预测原理及模型的改进
由于历史数据在采集过程中受到数据传输或者测量设备的影响,将无法避免许多不良数据或坏数据的存在。如果在负荷预测建模过程中使用这些数据,必然会在预测过程中带来误差,导致预测精度下降,所以在利用这些数据前需要对数据进行预处理,将不良数据剔除以确保综合预测的精度。
1.2 改进灰色预测模型
灰色建模是对历史数据进行累加生成后建立微分方程模型,由离散的灰色数列建立的模型即为灰色模型GM[4],它具有要求负荷数据少、不考虑分布规律和建模简单等优点。但GM存在数据离散程度较大时,预测精度相应变差的缺点。基于这种思想,出现了一种基于灰色系统模型GM(1,1)的 参数修正的预测方法[5],它相比传统灰色模型有更好的预测效果。
1.3 改进灰色—马尔科夫预测模型
灰色系统模型GM(1,1)其预测解为指数曲线,预测值的几何图形是要么单调递减,要么单调递增的平滑曲线,数据拟合效果可能对随机波动性大的数列达不到预期效果。而马尔科夫法的状态转移概率能够反映各随机因素的影响程度以及各状态间转移的内在规律。所以灰色预测和马尔科夫预测可以相互弥补不足,形成灰色—马尔科夫预测法[6]。
本文将马尔科夫理论结合灰色理论应用到短期负荷预测中,采用如下建模步骤。
(1)首先根据已知的一个月30天负荷数据建立改进灰色预测模型,对该月每天每时刻的负荷值进行预测,得到该月30天每个时刻的预测负荷值,并计算出该月各时刻预测值的相对误差eit,用于对预测日进行马尔科夫预测;
(2)选取这30天其中一个时刻的全部预测值,根据预测出的相对误差值划分变动区间[θ1,θ2],并根据变动区间划分若干状态空间Ei(i=1,2…n),其中状态空间表示为 Ei∈[θ11,θ21],…Ei∈[θ1i,θ2i],…,Em∈[θ1m,θ2m]。
选择合适的步长后,就可以得到该时刻以改进灰色理论预测模型得到的各时刻预测精度的状态。同理,得到预测日全天各时刻预测精度的状态。
(3)构造状态转移概率矩阵P(k)。

状态转移概率矩阵P(k)反映了系统各状态之间的转移概率。于是,马尔科夫链就可以确定了。
(4)确定了系统未来状态转移后,就确定了预测值的相对变动区间[θ1i,θ2i]。选择判断预测误差较大预测值,根据初始状态Ei和状态转移概率矩阵P(k)确定该时刻的预测状态,并进行预测校正:
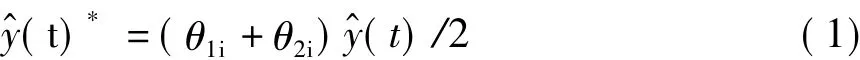
1.4 改进灰色—马尔科夫预测模型算例分析
本文首先选取2009年9月1日~10月1日东营市电网各时刻的历史负荷及其预测负荷作为训练样本集,得到9月1日~10月1日各时刻预测误差值;然后选取9月1日~29日的预测负荷值作为改进灰色-马尔科夫模型的样本值,并划分状态空间;最后对9月30日及10月1日时刻数据进行马尔科夫校验,并对模型的精度进行评价。
我们现以选取9月1日~29日每天的11:15时刻负荷数据为例,首先使用该时刻29天的改进灰色预测负荷值;然后根据所求相对误差划分4个状态区间为:E1∈(0,2],E2∈( - 2,0],E3∈(2,∞ ],E4∈其他;最后对9月30日及10月1日运用马尔科夫法进行预测校正。
2009年9月1日~29日改进灰色理论法预测值与真实值比较可以确定状态转移矩阵:

由于29日11∶15点负荷处于E2状态,我们可令其初始向量为 V0=[0 1 0 0],则 V1=V0,P(k)=[0.1667 0.5 0.1667 0.1667],故预测得30 日11∶15点负荷处于E2状态;
同理,10 月 1 日状态 V2=V0,P(k)2=[2.2381 0.3125 0.2203 0.2292],故预测1 日负荷处于 E1状态;此时,对原预测结果按公式(1)进行修正。
这两日的马尔科夫法预测校正数据示于表1。

表1 马尔科夫法校正前后预测负荷比对表
由上表可以看出,9月30日11∶15时刻预测相对误差由-0.0005改进后增加为-0.0025,10月1日预测误差由0.0031改进后下降为0.0011。因为马尔科夫校正法存在一定的随机性,所以不能保证经过马尔科夫校正后预测值误差均小于 的预测值皆通过马尔科夫法校正,所有时刻皆采用马尔科夫校正算法校正误差较大的时刻。
图1为2009年10月1日改进灰色-马尔科夫理论法预测值与灰色预测值比较曲线。
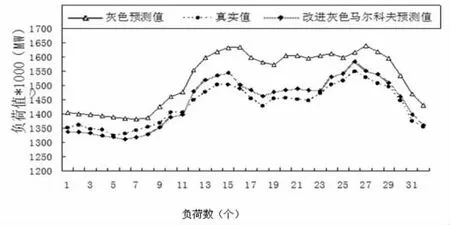
图1 2009年10月1日预测值的比较曲线
从上图的对比中可以看出,经过马尔科夫校正后的预测曲线明显比灰色预测曲线接近真实值。从图中看出改进灰色马尔科夫预测误差值在±2.5%以内,相比灰色预测误差明显减少,表明经过马尔科夫校正后预测精度明显提高,该方法可行。
2 短期负荷预测综合预测模型
2.1 综合预测原理及模型
综合预测是在几种不同预测方法的基础上,选择适当权重,对预测结果进行加权平均。因此确定综合预测中各个预测方法的权重系数成为综合预测方法的关键。综合预测模型的准确度也由不同的单一预测模型的权重系数决定。目前,采用移动样本的适应性的实时算法成为解决变权值问题的主要方法[7-8],其权重系数是由最近的 s个样本历史值来计算得到。常用的算法是

式中,eit为各种预测方法在不同时刻的相对误差,k是单一预测模型的个数。
这一算法的移动样本为据预测日最近的s个样本的历史值,并且由此求得权系(i=1,2,…,k)。
2.2 综合预测算例分析
根据东营市全网2009年9月1~30日负荷情况,我们首先通过9月1日~30日负荷值建立指数平滑、改进灰色—马尔科夫以及神经网络预测模型,对10月1日负荷值进行预测。预测值与10月1日实际值比较计算得相对误差,并根据时变权系数法确立各个预测模型的权值;然后利用9月2日~10月1日负荷值建立10月2日的各个时刻单一预测模型;最后根据已确定的权重系数与各个单一预测模型建立综合预测模型,对2009年10月2日负荷情况进行综合预测。其预测样本为2009年9月2日~10月1日历史负荷值。图2为2009年10月2日四种预测曲线的对照。
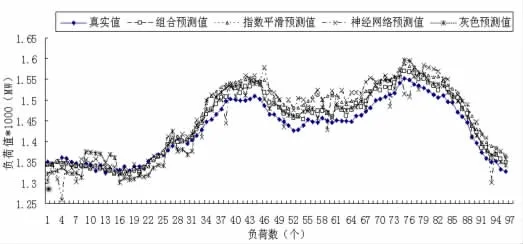
图2 2009年10月2日四种预测曲线的对照
图3为10月2日四种预测模型相对误差对比结果。
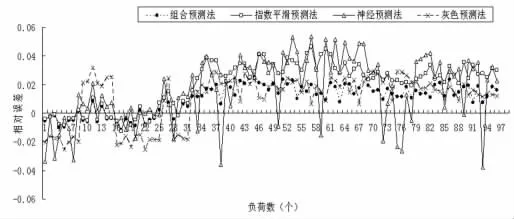
图3 2009年10月2日四种预测误差曲线的对照
从上述预测结果可以看出,综合预测模型的预测曲线更接近于实际的负荷曲线,而单一方法的预测结果则有可能出现较大偏差。从表2可以看出,综合预测法最大相对误差为2.72%,最小相对误差为0.04%,平均相对误差1.1%,均小于其它单一预测方法。所以综合预测模型的预测结果是令人满意的,可以得到更好的预测结果。
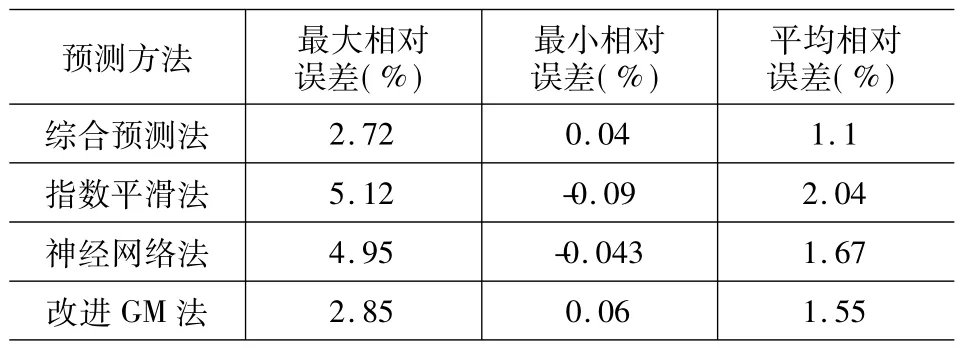
表2 各种预测方法误差值比较
3 结语
本文提出了一种改进灰色-马尔科夫预测校正模型,提高了负荷预测精度,并且建立基于指数平滑、人工神经网络和改进灰色-马尔科夫预测校正模型的综合预测模型,以满足复杂电力负荷系统短期负荷预测的要求。
[1] 史文江,黄伟,魏志连等.基于短期负荷预测的无功/电压控制策略研究[J].保定:现代电力2008,25(4):11-14
[2] 李艳芳.电力负荷预测技术的研究与应用[D].杭州:浙江大学.2005
[3] 陈国栋.电网规划中负荷预测的分析与研究[D].长沙:湖南大学.2008
[4] 唐杰明,刘俊勇,杨可等.基于灰色模型和最小乘支持向量机的电力短期负荷组合预测[J].北京:电网技术,2009,3(22):63-65
[5] 陈灿,刘新东.一种新的电力系统短期负荷预测方法[J].武汉:软件导刊,2010,7(9),8:10
[6] 刘克文.电力系统短期负荷预测方法研究及实现[D].保定:华北电力大学.2010
[7] 谢开贵,李春燕,周家启.基于神经网络的负荷组合预测模型研究[J].北京:中国电机工程学报,2002,22(7):85-89
[8] Sun D I,Ashley B,et al Optimal Power Flow by Newton Approach.IEEE Trans on PAS,1984,103(10):2864-2880
