从头计算研究BCl+基态和激发态的势能曲线和光谱性质*
2013-08-22于坤1张晓美2刘玉芳2
于坤1)2) 张晓美2) 刘玉芳2)†
1)(兴义民族师范学院物理系,兴义 562400)
2)(河南师范大学物理与电子工程学院,新乡 453007)
(2012年10月29日收到;2012年11月19日收到修改稿)
1 引言
卤代硼化物在半导体材料、金属蚀刻和微电子器件制造等过程中起着非常重要的作用[1,2].由于卤代硼化物与金属表面相互作用的过程中会产生大量的中性BCl自由基以及它的阳离子BCl+,所以通过研究BCl和BCl+的物理化学性质有助于人们理解卤代硼化物在工业过程中的反应机理.
BCl和BCl+在分子反应中的物理化学性质已经引起了研究者的广泛关注,许多研究者试图通过研究它们的光谱特性和电子结构来探究其在反应过程中的重要作用[3-11].Hildenbrand[9]通过实验确定了BCl+基态离解能为3.53 eV±0.11 eV.Bauschlicher和Ricca[10]进行了理论B3LYP/6-311+G(2df)级别的从头计算确定了BFn,BF+n,BCln和BCl+n(n=1—3)的几何结构和振动频率.Irikura等[11]通过从头计算EE-EOM-CCSD方法结合相关一致aug-cc-pVTZ基组确定了BCl+基态的光谱参数 Re,ωe,ωeχe.然而,对于 BCl+分子的电子结构和光谱性质,前人的工作仅仅局限于对BCl+基态的研究[9-11],关于激发态的研究还未见报道.最近,虽然我们对BCl自由基的电子结构进行了深入的研究[8],但是对于BCl+激发态的势能曲线和光谱性质还未进行过研究.
本文利用了能够充分考虑动力学相关的内收缩多参考组态相互作用方法计算了BCl+自由基的基态和13个激发态的势能曲线,为了得到更加准确的势能曲线,计算中考虑了Davidson矫正和标量相对论修正以及BCl+自由基的4个Λ-S自旋轨道耦合效应.利用LEVEL8.0程序拟合了束缚Λ-S态和Ω态的光谱参数,并与已有的Λ-S态X2Σ+的实验结果进行了对比,从而验证了本文计算结果的可靠性.文中首次计算得到的数据不仅为实验上研究BCl+复杂的光谱性质提供了相关的电子结构信息,而且也为相关体系的分子反应动力学[12,13]研究提供了可靠的理论依据.
2 计算方法
本文所有涉及BCl+自由基电子结构的计算均使用了专业的量子化学Molpro程序2010.1版本[14].基于该程序计算得到的势能曲线,使用LEVEL8.0程序[15]通过求解径向的Schr¨odinger方程得到了束缚态的光谱参数.
对于BCl+自由基,选取非收缩的高斯型全电子加弥散相关一致4zeta价基[aug-cc-pVQZ]作为B:13s7p4d3f2g和 Cl:17s12p4d3f2g的计算所用基组;选取步长为0.05˚A,核间距0.8˚A到6.0˚A的105个点进行能量扫描.每个单点能的计算依次使用如下三步计算方法:首先,利用单组态的Hartree-Fock(RHF)方法计算了BCl+的基态X2Σ+,生成基态的波函数;然后利用全活性空间自洽场方法(CASSCF)[16,17]对生成的基态波函数进行优化;最后利用内收缩多参考态相互作用方法(MRCI)[18,19]进行动力学相关能的计算进而得到相应的势能曲线,进一步提高势能曲线的质量.计算过程中还考虑了Davidson矫正(+Q)和标量相对论效应.
由于MOLPRO程序自身的限制,计算中使用了C∞ν群的子群C2ν群.C2ν群拥有4个不可约表示,分别是 A1,B1,B2,A2.在计算过程中 BCl+自由基的9个轨道被选为活性空间,包括5个a1,2个b1和2个b2对称性的分子轨道,它们对应B原子的原子轨道2s2p和Cl原子的轨道3s3p.B+的外层电子2s2和Cl的外层电子3s23p5被放置在活性空间内,剩下的12个电子被冻结而不进行相关能的计算.也就是说,在计算过程中,BCl+的9个电子参与了相关能的计算.
自旋轨道相互作用的研究[20,21]借助于MRCI+Q计算之后的全电子的Breit-Pauli哈密顿计算,计算中利用的是态相互作用,即通过在电子哈密顿本征函数基中对角化电子哈密顿本征函数和自旋轨道哈密顿本征函数之和获得自旋轨道本征态.其中哈密顿矩阵元Hel和HSO分别来自于MRCI+Q和CASSCF计算.自旋轨道相互作用使得BCl+自由基能量较低较为稳定的4个Λ-S态分裂成为7个Ω态,随后给出了相应的Ω态的势能曲线.
在计算得到Λ-S和Ω态的势能曲线以后,通过求解径向的核的Schr¨odinger方程得到了束缚态的光谱常数,包括离解能De,平衡核间距Re,激发能Te,振动常数ωe和ωeχe,平衡转动常数Be.同时为了说明Λ-S电子态的多组态性质,还给出了Re处主要的电子组态以及相应的权重.通过分析这些电子组态还可以得到形成Λ-S态所满足的跃迁规则.
3 结果与讨论
3.1 Λ-S态的势能曲线和光谱参数
利用多参考组态相互作用方法结合相关一致aug-cc-pVQZ基组计算得到了14个Λ-S态的势能曲线,包括8个双重态和6个四重态,这些态均为束缚态.它们分别对应两个离解极限B+(1Sg)+Cl(2Pu)和B(2Pu)+Cl+(3Pg),离解极限见表1,计算的MRCI+Q绝热势能曲线见图1.利用LEVEL8.0程序对束缚Λ-S态进行拟合得到的光谱参数列于表2,表2同时还给出了每个束缚态在平衡位置处主要的电子组态及相应权重.

表1 BCl+自由基Λ-S态的离解极限

图1 BCl+自由基的Λ-S态的势能曲线 (a)二重态;(b)四重态

表2 BCl+自由基的Λ-S态的光谱参数
自由基BCl+的基态X2Σ+的主要组态是1σ22σ21π43σα2π04σ05σ0,是一个深势阱的束缚态,其势阱深度为3.54 eV,与Hildenbrand[9]实验测到的BCl+的离解能值3.53 eV±0.11 eV非常符合.与文献比较发现,我们计算的光谱参数与Bauschlicher和Ricca[10]的结果非常接近.平衡核间距的差别仅仅是0.002˚A,振动常数ωe的差别也非常小,只有5.49 cm-1.在Irikura等[11]的理论计算结果中,Re值与我们的结果也很相符,但是ωe的值差别较大,非谐性常数ωeχe差别也较大.这可能是因为使用了cc-pVTZ基组考虑的相关能不足导致的. 和基态持有相同的离解极限B+(1Sg)+Cl(2Pu)的电子态还有第一激发态2Π(I).与基态相比2Π(I)是一个浅势井的束缚态,深度仅仅有0.8 eV,平衡位置的电子结构为1σ22σ21π2α3σ22π04σ05σ0,分析组态可以确定该态是基于基态的1π→3σ单电子激发形成的.文中2Π(I)态的光谱参数为首次报道,预测得到的电子态2Π(I)的能量最小值Te为22286.99 cm-1处于较大的核间距2.275˚A的位置.计算的振动常数ωe和ωeχe分别为311.30和3.09 cm-1.
B原子基态2Pu和Cl+离子的基态3Pg通过相互作用可以形成6个双重态和6个四重态,通过计算确定了它们之中能量最低的电子态为2Π(II),激发能Te=40543.54 cm-1,在平衡位置处的电子结构主要是 1σ22σ21π43σ02πα4σ05σ0.预测该态的离解能为3.1737 eV,表明该态的势阱较深,说明BCl+自由基在参与化学反应中处于该态的可能性较大.基态1π→2π的单电子激发可形成2Σ-(I),2Σ-(II)和2Δ,其中2Σ-(I)和2Δ的势能曲线几乎完全重合.它们的平衡核间距Re相同,绝热激发能Te也非常接近,分别为46812.18和46411.20 cm-1,振动常数ωe的差别也仅为2.67 cm-1.此外,从表1可以看出2Δ态的平衡位置处具有多个权重较大的电子组态,从而表明了采用多参考组态方法的必要性.2Π对称性的第三个根2Π(III)是基于基态的1π→4σ电子激发形成的,具有较高的能量和较浅的势阱,它的激发能Te=61819.86 cm-1,离解能De为0.53 eV.
与6个二重的Λ-S态对应的是6个四重Λ-S态,它们之间的区别在于电子组态中电子的自旋排列方式不同,所以这些态形成的激发方式与二重态一致.在四重态中,能量最低的电子态为4Σ+,激发能为42100.94 cm-1,略高于2Π(II)的激发能40543.54 cm-1.值得注意的是它的势能曲线与4Σ-(I)和4Δ的势能曲线也非常靠近,所以它们的光谱参数比较接近.4Δ和4Σ-(I)的激发能为44232.92和45750.14 cm-1,三者的势阱深度也相当,分别是 2.97,2.70和 2.47 eV.其余三个 Λ-S 态4Σ-(II),4Π(I)和4Π(II)的能量都比较高,激发能都集中在60000 cm-1附近,其中4Π(II)的能量最高,Te为64905.23 cm-1.而且4Π(II)存在一个不明显的势垒,位于键长3.14˚A处,这个势垒是由于4Π(II)与比它能量更高4Π对称性的电子态之间的避免交叉而形成的,并且这个势垒还导致了4Π(II)具有两个势阱,但由于这两个势阱都特别浅,很难在图1中观测到.表2中的光谱数据是通过拟合Re较小的那个势阱得到的.
3.2 Ω态的势能曲线和光谱参数
在考虑旋轨耦合效应的情况下,计算得到了7个Ω态的势能曲线,包括4个1/2态和3个3/2态.这7个Ω态对应的原子基态的离解极限能量从低到高依次为:B+(1S0)+Cl(2P3/2),B+(1S0)+Cl(2P1/2)和B(2P1/2)+Cl+(3P2).我们计算的Cl基态Cl(2P3/2)和第一激发态Cl(2P1/2)的能量差为910.57 cm-1,与相应的实验值882.35 cm-1比较接近.计算的Ω态的离解极限都列在了表3中,计算得到的Ω态势能曲线见图2,拟合的光谱参数以及Λ-S态组成成分列于表4.

图2 BCl+自由基的Ω态的势能曲线 (a)Ω=1/2电子态;(b)Ω=3/2电子态
基态Ω态为1/2态,在平衡位置处几乎完全来自于X2Σ+态,考虑旋轨耦合效应以后,基态的势阱深度由原来的3.54 eV变为3.50 eV,其他的光谱参数几乎没有发生变化.对于第一激发态Ω=3/2(I)来说,在平衡位置几乎完全来自2Π(I)态,其激发能Te为22014.40 cm-1位于键长2.241˚A处,和2Π(I)的光谱参数都非常接近,势阱深度与2Π(I)也几乎相同.1/2对称性的第二个根也为束缚态,其势阱较浅,离解能De=0.79 eV,光谱参数同Ω=3/2态几乎相同,在平衡位置处的Λ-S态成分以及权重分别为2Π(I)(92.6%)和X2Σ+(5.1%).在键长2.299˚A处,其势能曲线与基态的1/2态的势能曲线存在非常明显的避免交叉,这是由于考虑了旋轨耦合效应引起的.

表3 BCl+自由基Ω态的离解极限
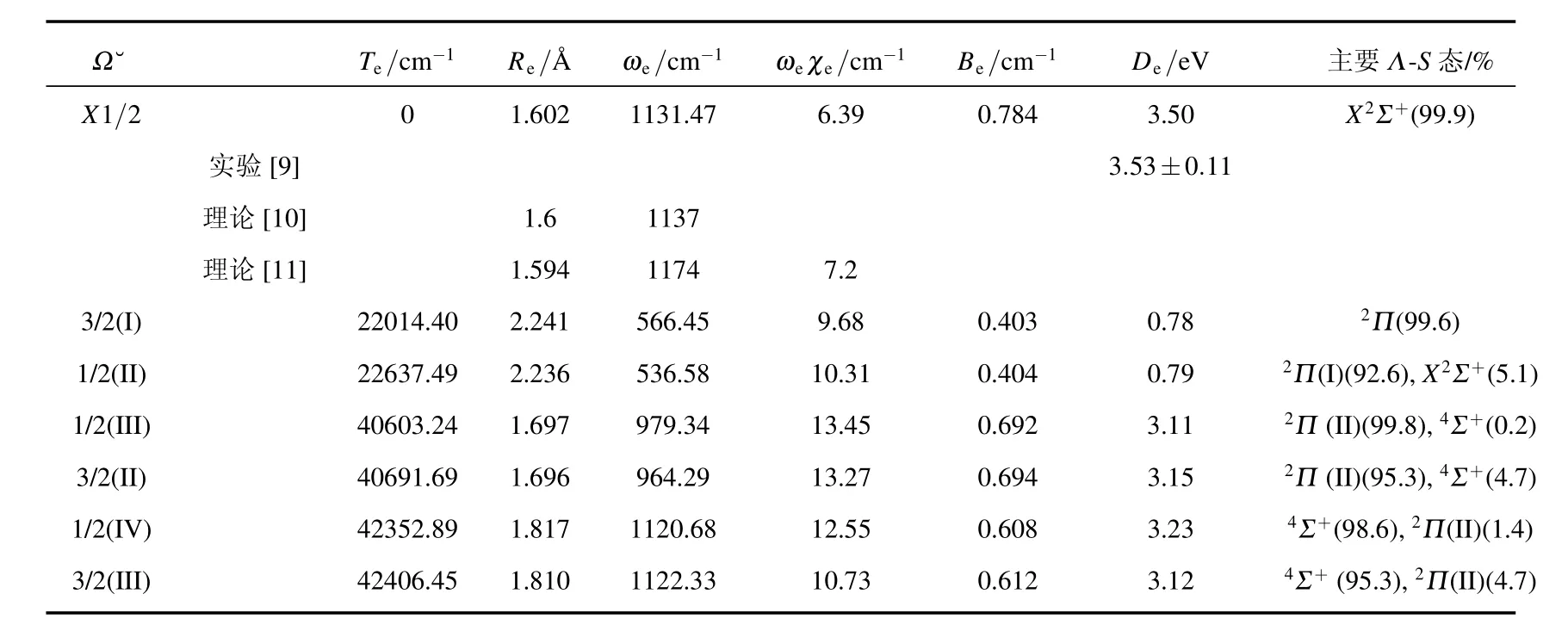
表4 BCl+自由基的Ω态的光谱参数
另外四个Ω态包括2个3/2态和2个1/2态,它们对应相同的离解极限B(2P1/2)+Cl+(3P2),势阱都较浅.Ω态1/2(III)和3/2(II)主要是通过2Π(II)分裂形成的,由于自旋轨道相互作用较弱,在计算中被视为微扰,故这两个Ω态的激发能差别很小,计算得到的激发能Te差别只有88.45 cm-1,其余的光谱参数也很接近.4Σ+分裂形成了两个Ω态 1/2(IV)和 3/2(III),它们的情况与 1/2(III)和3/2(II)类似,这里不再赘述.值得指出的是1/2(III)和1/2(IV),3/2(II)和3/2(III)的势能曲线分别出现了明显的避免交叉(见图2),这同样是由于考虑了自旋轨道相互作用引起的.
4 总结
本文利用了考虑标量相对论效应的多参考组态相互作用方法(MRCI+Q)和相关一致极化价基aug-cc-pVQZ计算了0.8—6.0˚A核间距范围的14个Λ-S态的势能曲线,获得的14个Λ-S态分别对应两个离解极限B+(1Sg)+Cl(2Pu)和B(2Pu)+Cl+(3Pg).旋轨耦合效应使得能量最低的4个ΛS态分裂成了7个Ω态,并导致Ω态的势能曲线产生了非常明显的避免交叉.通过求解径向的Schr¨odinger方程得到了Λ-S态和Ω态的光谱参数.计算得到Λ-S态的基态结果与实验符合得非常好.值得注意的是,除基态外,其余13个Λ-S态和Ω态的光谱常数均为首次报道.此外,本文还给出了每个Λ-S态的电子结构性质,通过分析它们的电子结构特性,我们得到了各态的电子跃迁特性.同时,所给出的束缚态主要组态和权重也体现出了这些电子态的多组态性质,表明了使用多参考态方法的必要性.本文的计算结果为实验上研究BCl+复杂的光谱性质提供了一定的理论依据和参考.
[1]Flamm D L 1993Solid State Technol.36 49
[2]Patron S J,Hobson W S,Abernathy C R,Ren F,Fullowan T R,Katz A,Perle A P 1993Plasma Chem.Plasma Proc.13 311
[3]Huber K P,Herzberg G 1979Molecular Spectra and Molecular Structure IV:Constants of Diatomic Molecules(New York:VanNostrand Reinhold)
[4]Maki A G,Lovas F J,Suenram R D 1982 J.Mol.Spectrosc.91 424
[5]Bredohl H,Dubois I,Houbrechts Y,Nzohabonayo P 1984 J.Phys.B:At.Mol.Phys.17 209
[6]Bredohl H,Dubois I,M´elen F 1987 J.Mol.Spectrosc.121 135
[7]Verma R D 1995 J.Mol.Spectrosc.169 295
[8]Liu Y F,Zhang X M,Yu K 2012 Computat.Theor.Chem.991 82
[9]Hildenbrand D L 1996 J.Chem.Phys.105 10507
[10]Bauschlicher C W,Ricca A 1999 J.Phys.Chem.A 103 4313
[11]Irikura K K,Johnson R D,Hudgens J W 2000 J.Phys.Chem.A 104 3800
[12]Wang X Y,Ding S L 2004 Acta Phys.Sin.53 423(in Chinese)[王晓艳,丁世良2004物理学报53 423]
[13]Han H X,Peng Q,Wen Z Y,Wang Y B 2005 Acta Phys.Sin.54 78(in Chinese)[韩慧仙,彭谦,文振翼,王育彬2005物理学报54 78]
[14]Werner H J,Knowles P J,Lindh R.Manby F R,Sch¨utz M,Celani P,Korona T,Rauhut G,Amos R D,Bernhardsson A http://www.molpro.net.[2012-10-29]
[15]Le Roy R J 2007 LEVEL 8.0:A Computer Program for Solving the Radial Schr¨odinger Equation for Bound and Quasibound Levels.University of Waterloo Chemical Physics Research Report CP-663
[16]Werner H J,Knowles P J 1985 J.Chem.Phys.82 5053
[17]Knowles P J,Werner H J 1985 Chem.Phys.Lett.115 259
[18]Werner H J,Knowles P J 1988 J.Chem.Phys.89 5803
[19]Knowles P J,Werner H J 1988 Chem.Phys.Lett.145 514
[20]Yan B,Pan S F,Wang Z G,Yu J H 2005 Acta Phys.Sin.54 5618(in Chinese)[闫冰,潘守甫,王志刚,于俊华2005物理学报54 5618]
[21]Li R,Lian K Y,Li Q N,Miao F J,Yan Bing,Jin M X 2012 Chin.Phys.B 21 123102
[22]Moore C E 1971 Atomic Energy Levels(Washington,DC:National Bureau of Standards)
