基于动平衡机有限元模型的无试重动平衡方法

周 瑾，王玉龙，郭勤涛

(南京航空航天大学机电学院，江苏 南京 210016)

目前广泛运用的转子动平衡设备大多是基于影响系数法双面动平衡原理，需要对转子进行试加重，测得加重对转子不平衡响应的影响，计算出应加的平衡配重.随着工业技术的发展，人们对动平衡的效率提出了更高的要求，运用传递矩阵法或有限元建模仿真技术实现无试重动平衡，只需开机一次，就能完成动平衡过程［1－6］.传递矩阵法必须对设备的各个部件进行大量的简化，才能建立数学模型，离散化不够细致，即使获得较准确的材料参数和结构参数，将这些参数代入经过大量简化的数学模型，也无法获得与实际设备较为吻合的不平衡响应特性，从而影响了动平衡的准确性.随着数学、力学等基础科学的不断发展，特别是计算机技术的发展，为有限元法提供了发展的基础，有限元法已经成为结构分析最为简便、最为准确的数值分析方法之一［6－9］.

文中拟以软支承动平衡机为研究对象，建立动平衡机有限元模型，并从软支承动平衡机基础上测得初始不平衡响应信号;在其有限元模型中进行配重，并求解出动平衡机上的不平衡转子应加的平衡配重;实现基于有限元模型的无试重动平衡方法，减少动平衡过程的开机次数，提高动平衡效率.

1 基于有限元模型无试重动平衡方法

进行无试重动平衡的具体步骤如下:

1)建立动平衡机有限元模型.

2)启动动平衡机，对其进行不平衡响应测试，获得转子两端的初始不平衡响应信号.对获得的信号进行带通滤波处理，读取信号峰值和相位，得到不平衡响应信号向量大小U0，V0.

3)在动平衡机有限元模型的两个平衡面Ⅰ，Ⅱ上分别试加虚拟配重P1，P2，测得两次试加虚拟配重后的不平衡响应信号.对获得的信号进行带通滤波处理，获得不平衡响应特征信号，读取信号峰值和相位，得到不平衡响应信号向量大小 A01，B01，A02，B02.

5)设平面Ⅰ和Ⅱ相应等效不平衡质量分别为Q1'和 Q2'，令平衡方程为

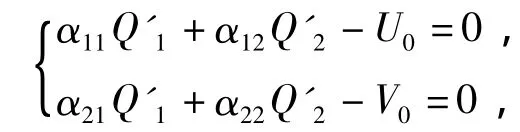
代入原始振动幅值、相位和影响系数，求解此方程组可解得 Q1'，Q2'.则 Q1'，Q2'可与待平衡转子中未知不平衡质量使转子产生相同的不平衡响应.在平衡面上取 Q1'，Q2'的对称质量 Q1，Q2，加入有限元模型中，可使有限元模型转子质量对称，减小乃至消除不平衡响应，Q1，Q2即为待平衡转子的平衡配重.

2 动平衡机的有限元模型

软支承动平衡机是最常见的用于转子动平衡的设备，其结构示意图见图1.转子有两个平衡盘，转子两端架于动平衡机两端摆架顶部的轴承上，摆架两侧用两根弹簧钢薄板悬挂于外部基座上，以电动机驱动转子.

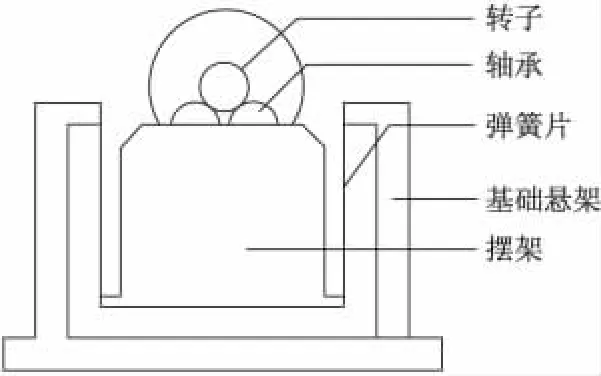
图1 软支承动平衡机结构

以梁单元建立的转子模型如图2所示，该转子自由状态下的一阶固有频率为623.9 Hz，相对于16.51 Hz(动平衡机的平衡转速)的转速较高，此转子可做为刚性转子考虑.Nastran中提供了建立转子单元的功能模块Rotor Dynamics，做转子的不平衡响应分析.选择梁单元建立转子模型，并在转子的任意位置增加适当大小的不平衡质量模仿转子中的未知不平衡质量.

图2 转子有限元模型

动平衡机两端的摆架(见图1)刚度较大，固有频率较高，动平衡机转速为16.51 Hz，系统的不平衡响应频率较低，因此，可将摆架作刚体考虑.两侧悬挂的弹簧片为薄片型钢板，以面单元仿真动平衡机的摆架和两侧弹簧钢片.用RBE2刚性连接单元约束转子与摆架之间的相对平动，保留相对转动的自由度，表示摆架上轴承与转子间的联接.动平衡机基座刚度较大，可将弹簧片与基座连接处的工况简化为固支状态.弹簧片与摆架连接处用RBE2刚性连接单元约束节点之间的平动与转动自由度，表示动平衡机上的螺栓连接.建立的软支承动平衡机有限元模型如图3所示.

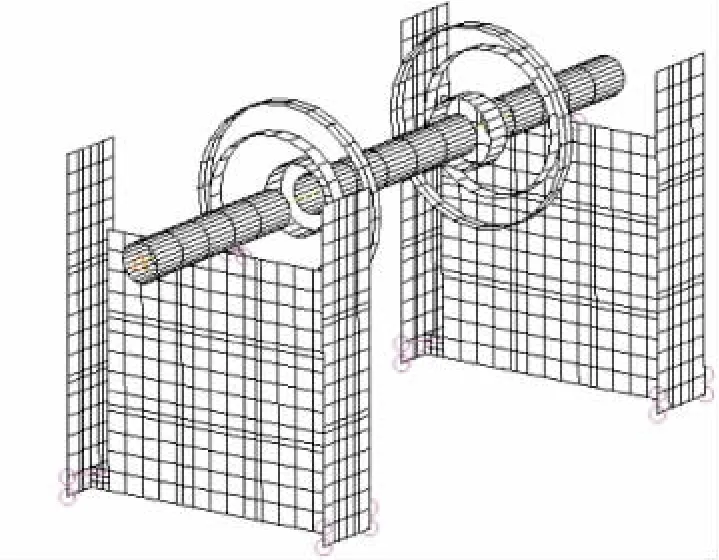
图3 软支承动平衡机有限元模型

3 无试重动平衡试验

图4为动平衡试验系统示意图.

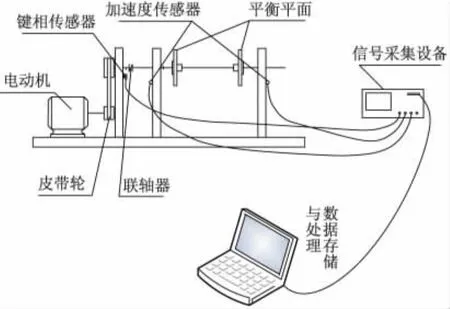
图4 动平衡试验系统

由图4可见，系统主要由软支承动平衡机、信号采集设备、计算机3部分组成.双盘转子两端架于动平衡机两端摆架的轴承上，两端摆架分别由两根弹簧片悬挂于基础悬架上，基础悬架为刚度较大的钢架.电动机通过皮带轮传动和联轴器传动带动转子转动.当转子上存在不平衡质量时，转子受不平衡质量产生的离心力作用产生振动，带动摆架和联轴器水平摆动.不平衡响应信号主要包含两个特征:幅值和相位.靠近联轴器处，安装有相位传感器，转子每旋转一周，产生一个脉冲信号.在两端摆架上各安装一个加速度传感器，测量摆架的振动.将3个传感器测得的模拟电信号即转子两端的不平衡响应的时域信号和定位零相位的基准信号，传输至信号采集设备HP35670频谱分析仪中，进行数字离散化处理并储存.然后将储存的数据导入微机中进行处理，利用Matlab程序进行带通滤波，保留与转速同频率的不平衡响应特征信号，并读取滤波后信号的峰值和相位.

启动动平衡机，对其进行不平衡响应测试，获得转子两端的初始不平衡响应信号U0=0.2069 m·s－2∠268.53°，V0=0.7921 m·s－2∠332.75°.在转子有限元模型的A，B端平衡面上分别增加虚拟配重P1=P2=5 g∠0°，对其做不平衡响应分析，导出两测点处的不平衡响应加速度时域信号，并做带通滤波处理，获得信号如图5所示.

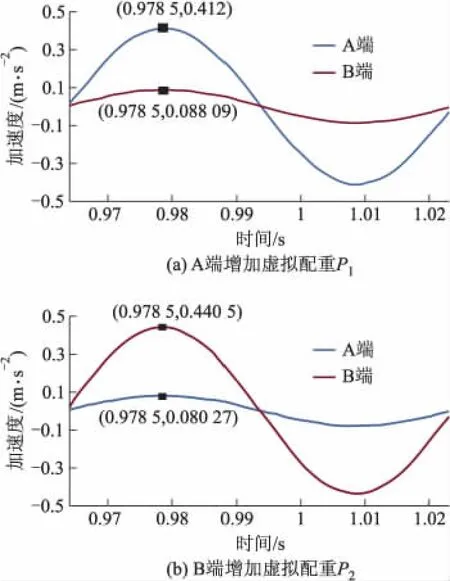
图5 有限元模型中增加虚拟配重后的两端振动加速度信号

A端增加P1后，A，B端振动向量信号为0.412 m·s－2∠268.53°和 0.08809 m·s－2∠268.53°;B端增加 P2后，A，B端振动向量信号为0.08027 m·s－2∠268.53°和 0.4405 m·s－2∠268.53°。

利用(1)－(3)式，求解出一组位于初始有限元模型转子平衡面上的与软支承动平衡机转子中的不平衡质量等效的不平衡质量Q1'=2.45 g∠317.95°，Q2'=9.141 g∠67.16°，取这组不平衡质量的对称质量:Q1=2.45 g∠137.95°，Q2=9.141 g∠247.16°，加入试验设备的两个平衡面内进行平衡，转子A，B端平衡前后振动加速度频谱如图6，7所示.

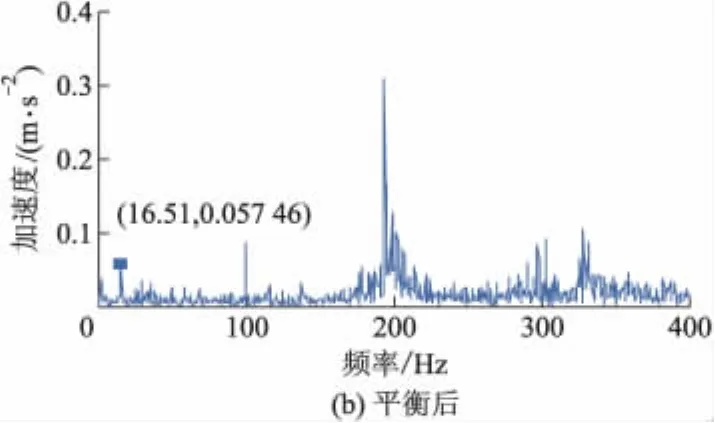
图6 转子A端振动加速度频谱

图7 转子B端振动加速度频谱

由图6，7可见，采用基于有限元模型的无试重动平衡后，转子A端不平衡响应特征信号的幅值降为 0.05746 m·s－2，为平衡前振幅 0.2215 m·s－2的25.9%，B 端振幅降为0.1319 m·s－2，为平衡前振幅0.7992 m·s－2的16.5%.同时，相应倍频处的幅值也大大减小.

4 结论

1)介绍了一种基于有限元模型的无试重动平衡方法.

2)以某一软支承动平衡机为例，通过模型简化，建立了该动平衡机的有限元模型.

3)在建立的动平衡机有限元模型基础上，根据刚性转子影响系数法双面动平衡原理，采集不平衡响应信号，实现无试重动平衡.试验表明，该方法实现了一次开机即可完成动平衡，提高了动平衡的工作效率.

References)

［1］Delgado E P，Bannister R H.Balancing of an experimental rotor without trial runs［J］.International Journal of Rotating Machinery，2002，8(2):99 －108.

［2］EI-Shafei A，EI-Kabbany A S，Younan A A.Rotor balancing without trial weights［J］.Journal of Engineering for Gas Turbines and Power，2004，126(3):604 －609.

［3］Rodrigues D J，Champneys A R，Friswell M I，et al.Automatic two-plane balancing for rigid rotors［J］.International Journal of Non-Linear Mechanics，2008，43(6):527－541.

［4］Niebsch J，Ramlau R，Nguyen T T.Mass and aerodynamic imbalance estimates of wind turbines［J］.Energies，2010，3(4):696 －710.

［5］邓旺群，唐 广，高德平.转子动力特性及动平衡研究综述［J］.燃气涡轮试验与研究，2008，21(2):57－62.Deng Wangqun，Tang Guang，Gao Deping.Research summary of rotor dynamic characteristics and dynamic balance ［J］.Gas Turbine Experiment and Research，2008，21(2):57－62.(in Chinese)

［6］王维民，高金吉，江志农，等.旋转机械无试重现场动平衡原理与应用［J］.振动与冲击，2010，29(2):212－215.Wang Weimin，Gao Jinji，Jiang Zhinong，et al.Principle and application of field balancing without trial weight for rotating machinery ［J］.Journal of Vibration and Shock，2010，29(2):212－215.(in Chinese)

［7］Saldarriaga M V，Jr V S，Hagopian J D，et al.On the balancing of flexible rotating machines by using an inverse problem approach［J］.Journal of Vibration and Control，2011，17(7):1021 －1033.

［8］王玉龙，周 瑾，郭勤涛.基于基础加速度响应的刚性转子在线双面动平衡有限元仿真研究［J］.机械与电子，2011(3):3 －6.Wang Yulong，Zhou Jin，Guo Qintao.FEM simulation of online two-plane balancing of rigid rotor based on accelerating unbalancing response on the basis［J］.Machinery and Electronics，2011(3):3－6.(in Chinese)

［9］章 云，梅雪松，邹冬林，等.应用动力学模型的高速主轴无试重动平衡方法［J］.西安交通大学学报，2011，45(7):34 －37.Zhang Yun，Mei Xuesong，Zou Donglin，et al.Modelbased balancing method for high-speed machine tool spindle without trial weights［J］.Journal of Xi’an Jiaotong University，2011，45(7):34－37.(in Chinese)