基于灰关联分析和证据理论的多传感器目标识别方法

潘智宗

（中国人民武装警察部队工程大学 信息工程系，陕西 西安 710086）

0 引言

在振动传感器对桥梁、仓库等进行监视和战场探测等应用中，目标识别是重要的环节之一。由于信号到达传感器阵列的时间和幅值不同，即使是同一种目标运动引起的振动信号在同样的检测范围内得到的信号都会有较大的差别。因此，各传感器提供的信息往往包含着大量的不确定性，给快速识别目标类型带来了很大困难。信息融合技术可以综合多个传感器的数据来确定目标的特征参数，但单一的数据融合方法具有局限性，不能很好地解决干扰存在下的目标分类识别问题。为了提高目标识别的正确率，本文提出了一种基于改进的灰关联分析和证据理论的振动目标识别方法。先由改进后的灰色联分析法得出各传感器的基本概率赋值，再利用基于基本概率赋值的决策准则来识别振动源的类型。

1 改进的灰关联算法

灰关联分析是按发展趋势进行分析，对样本量大小没有太高的要求，分析时也不需要典型的分布规律，且分析结果一般与定性分析相吻合。因而采用灰关联分析方法对现有少量侦查数据进行综合分析，可为实时、准确地进行辐射源识别提供理论基础和数学依据。

但传统的灰色关联算法也有其自身的局限性。例如，特征指标权重的选取是人为给定的，主观因素较大，过于经验化和绝对化；灰关联分析是针对数据精确数的情形，不能体现出传感器获得的信息是模糊、不确定的特点。为此，本文以区间数来表征目标类型的特征指标值和传感器测量值，利用区间灰关联度和熵权提出了一种不确定融合算法。

1.1 区间灰关联

针对传感器目标识别问题，设其目标类型集为：s=｛s1，s2，……，sm｝，每个目标类型包含的特征指标集为：p=｛p1，p2，……，pm｝。针对目标类型 si按属性 pj进行测量，得到 si关于 pj的属性值为区间数从而构成特征指标矩阵：

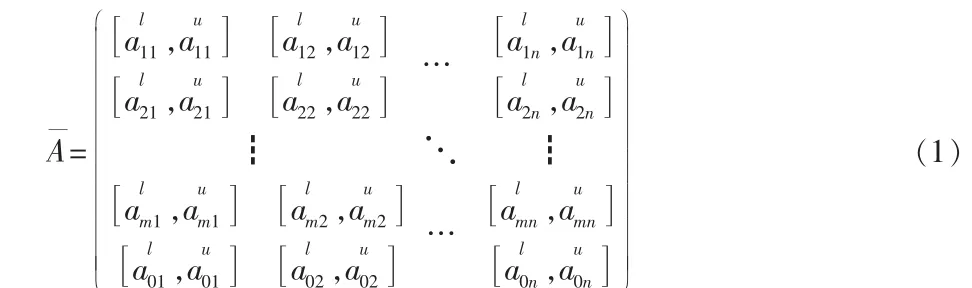
由此可得识别目标类型与待识别目标距离矩阵为D＝（dij）m×n，其中

则根据灰色关联理论，区间灰关联系数可定义为：

由（4）式可得，各目标类型与未知目标X的区间灰关联系数矩阵为 ξ=（ξij）m×n

若特征属性权重向量 W=｛w1，w2，…，wn｝已知，则目标类型 si与 X的区间灰关联度为：

γi反映了X与si的相似程度，γi越大，表明X与si越相似，即未知目标X属于目标类型si的可能性越大。本文中权重的确定采取文献[4]的熵权法获取。

2 证据理论的基本知识

2.1 证据组合规则

假设辐射源识别框架为 U=｛R1，R2，…，Rn｝，其中 Ri代表不同类型的辐射源。D-S证据理论用识别框架 U表示所感兴趣的命题集，它定义识别框架 U上的基本概率赋值函数m：2U→［0，1］，满足：

式中，命题 A是 U的非空子集，称为焦元，m（A）反映了对命题 A信任的程度。

如果m1，m2，…，mn是在同一识别框架 U上根据n个独立振动传感器的证据所获得的基本概率赋值函数，则可以利用式（8）的Dempster组合规则计算出这n个证据共同作用下的基本值函数：

2.2 基于基本概率赋值的判决准则

用证据理论组合证据后如何进行决策，是与具体应用密切相关的问题。常用的决策方法有基于信任函数的决策、基于基本小风险的决策。本文在融合不同振动传感器的证据后，采用基于基本概率赋值的决策，来识别不同类型的辐射源。假设U是识别框架，m是利用Dempster组合规则将n个不同电子侦察传感器的证据融合后的基本概率赋值。

假设存在∀A1，A2⊂U，满足：

若有

则A1为最终的辐射源识别结果，其中ε1、ε2为预先设定的门限，m（U）表示不确定结果的基本概率赋值。

3 目标识别算法的步骤

综合上述分析，下面给出基于多传感器多特征的目标识别算法，其具体步骤如下：

3.1 由（1）式得到各传感器对应的增广特征指标矩阵

3.2 由（3）式得到距离矩阵

3.3 由（4）式得到区间灰关联系数矩阵

3.4 利用（6）和（7）式得到属性权重向量

3.5 由（5）式得到各目标类型与未知目标X的区间灰关联度

3.6 获取基本概率赋值函数，其公式如下：

其中，m（U）是不确定结果的基本概率赋值。

3.7 根据Dempster组合规则融合多个证据体基本概率赋值

3.8 根据（8）和（9）做出判决

4 应用举例

假设振源识别框架为U=｛大车，小车，人｝，选取过零数、信号功率谱和信号持续时间作为特征参数。参考数列通过各传感器的实时探测获取，比较数列为振源数据库中各振源数据。表1给出了U中各振源的特征参数，表2为3个振动传感器获得的对大车的3组测量值θij和标准方差δij（括号内为标准方差）。

表1

由此便可以上述方法计算出各传感器的对于各目标类型的基本概率赋值及证据融合后的结果，如表2所示。

在表2中根据三个传感器的基本概率赋值进行证据融合，最终得到判决结果是大车。由此可见，本算法通过灰关联理论和D-S证据理论融合了多个传感器的数据来确定目标的特征参数，克服了单一的数据融合方法具有局限性，能有效地解决干扰存在下的目标分类识别问题。

表2

5 结束语

本文提出了通过区间灰色关联算法获取多个传感器证据的基本概函数，根据证据理论融合多个传感器的证据，采用基于基本概率赋值的决策准则来识别振动源的方法。该方法将传感器的测量值和目标特征参数模糊化，用区间数来表达不确定性，提出了基于区间灰色关联的数据融合方法，利用熵权克服了传统方法中属性权重选取的主观性问题，使得目标识别结果具有可信度高、更加符合实际的优点，为解决多传感器信息融合问题提供了新的途径。

［1］李楠,曲长文，等.灰色关联理论在辐射源识别中的应用[J].系统仿真学报,2009(78)：96-98.

［2］Da R,Lin C F.A new failure detection approach and its application to GPS autonomous integrity monitoring[J].IEEE Trans.on Aerospace and Electronic Systems,1995,31(l)：499-506.

［3］赵艳玲，门丽洁.基于灰色关联分析的舰船目标分类识别[J].舰船科学技术,2009,31(10)：36-38.

［4］林云,司锡才，等.改进灰色关联算法在辐射源识别中的应用[J].通信学报,2010,31(8A)：166-171.

［5］刘君华,汤晓军，等.智能传感器系统[M].西安：西安电子科技大学出版社,2010.