基于灰色BP神经网络的光伏发电系统最大功率点跟踪

曾令全，王 宏

(东北电力大学电气工程学院，吉林吉林132012)

光伏发电是一个直接将光能转化为直流电能的过程［1］，它被视为清洁型的发电能源。同时，光伏发电也是应用前景最广、可再生能力最强的一种能源。所以，学者们在十几年前就对光伏发电技术的研究产生了极大的兴趣。无论是独立的发电厂还是并网发电系统，光伏发电技术都以其逐渐提高电池转化效率及较高可靠性受到业内人士的广泛认可［2］。经过研究可知，光伏发电系统的输出电压与电流表现出一种非线性的关系，从这种非线性的关系可以看出，在给定的温度和光照条件下，光伏电池(PV)系统可以在某一点处输出最大功率，也称为最大功率点(MPP)。此外，由于PV系统的输出功率主要取决于当时天气的太阳光照以及周围环境的温度，MPP会随着太阳能电池所处的外部环境的变化而变化。因此，为实现光伏发电系统的高效率发电，必须考虑光伏电源与负载在不同天气状况下的合理匹配。目前为止，已经提出了很多可以实现MPP跟踪的技术，这些技术在各个方面的复杂程度各不相同，如:对传感器的要求、收敛速度、成本费用、适用范围、对硬件设施的要求、可普及度等方面。以往所提出的方法中［3］，较为常用的有恒压法、扰动观察法(简称P＆O法)、导纳增量法。在这些方法中，恒压法最为简单，但在温度变化时，恒压法往往无法跟踪到MPP，因此恒压法仅仅作为理论上一种跟踪MPP的方法，实际中并不常用。由于P＆O 法易于实施，因此在实际中较为常用［2］，但P＆O技术的一个缺点就是在稳定状态下，该方法所计算出的工作点会在最大功率点附近波动，这就会对已有能量造成浪费。导纳增量法和P＆O法具有相同的参数测量方法，但从该方法的推导上看，忽略了温度变化带来的影响。总的来说，在应对不断变化的环境情况下，这些传统的MPPT方法要想准确跟踪MPP还具有一定的困难。

本文提出了一种基于神经网络的MPPT控制算法。经过计算可以看出，与以往的BP神经网络法相比，该算法能够更加准确地对MPP进行跟踪。与以往提出的各种MPPT方法相比，灰色BP神经网络法更加简单，从算法本身的性质来看，该算法在一定程度上减轻了MPP的波动，也就相应地提高了太阳能的利用率。

1 PV阵列模型分析

首先，介绍一下光伏电池的数学模型，如图1所示。光伏电池可以看做电流源的非线性元件，产生一种与光照成正相关的电流，其中的两个电阻Rs和Rsh代表光伏电池功率损耗的等值电阻。串联支路的电阻Rs所造成的损耗是光伏电池表面的电阻损耗;并联支路Rsh所造成的损耗是由于太阳能电池内部的电流泄露造成的。

图1 简化太阳能电池电路

PV阵列由一系列串联或并联的光伏电池构成，随着太阳光照强度以及电池温度的变化，PV系统的I－V和P－V就会表现出非线性特征，式(1)给出了说明PV电池工作原理的数学模型:

式中:q为电荷量;n为依赖于光伏发电技术［3］的光伏电池的理想因子;k为波尔兹曼常数;Icell为电池的输出电流;Iph为依赖于电池工作温度及太阳光照强度的光生电流;I0为二极管的反向饱和电流;Rs为光伏电池的串联电阻;Tc为光伏电池的工作温度;Vcell为光伏电池的输出电压。其中光生电流Iph主要取决于太阳的光照强度以及电池的工作温度，即

式中:ISC为温度在25℃，太阳光照在1 kW/m2时的短路电流;Kl为短路电流的温度系数;G为太阳光照强度，kW/m2;T0为光伏电池的参考温度。从式(2)可以看出，光伏电池的饱和电流Is随着电池工作温度的变化而变化，即

式中:ISO为电池工作在参考温度以及光照强度为1 kW/m2时电池的反向饱和电流，Eg为电池内部的半导体能量的总和。ISO的计算表达式为

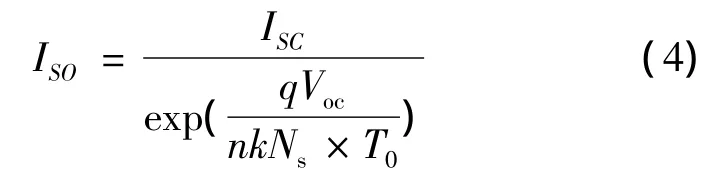
式中:Voc为光伏电池在标准工作情况下的开路电压，Ns为相关联(并联或串联)电池的数量。

由于PV元件的输出功率随着电池工作温度以及太阳的光照强度而变化，因此在对PV模型进行仿真时就必须将这些因素考虑进来，这里通过在Matlab的Simulink平台对模型进行仿真，图2、图3给出了在不同的光照强度及温度下PV系统的I－V及P－V曲线。

图2 不同光照水平下I－V及P－V特性曲线

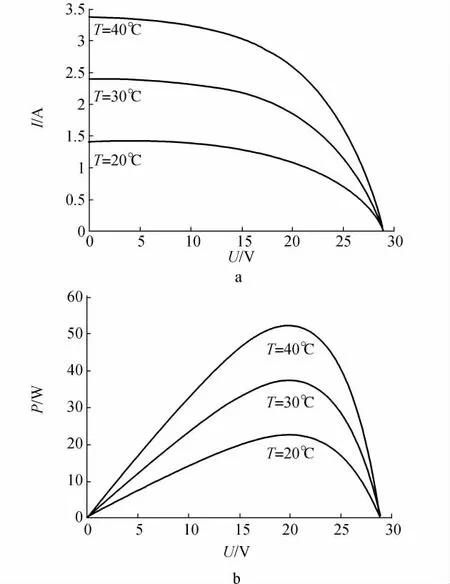
图3 不同温度下的I－V及P－V特性曲线

2 基于BP神经网络的MPPT控制器

最大功率点跟踪就是实时检测光伏阵列的输出功率，采用一定的控制算法预测当前工况下阵列可能输出的最大功率，通过调整功率控制器件PWM波的占空比，来改变当前电路的等效阻抗，使之永远工作在MPP附近，这一过程即称为最大功率点跟踪。

BP神经网络［4］是在人工神经网络(ANN)中常用的一种方法。该方法是一种监督性的学习方法，基本原理为:输入信号通过隐藏层节点作用于输出层节点，经过非线性变换产生输出信号，计算网络的输出信号与实际输出信号之间的误差，通过调整隐藏层与输入层节点之间的关联强度以及隐藏层与输出层节点之间的关联强度，使误差沿梯度方向下降，经过反复训练，直到确定出与最小误差相对应的网络参数，训练结束。

反向传播［5］是一个迭代的过程，其计算需要花费一定的时间，如果利用多核计算机的多线程技术来执行该算法，则可节约大量的计算时间。算法在计算机上更加容易利用多线程来实现，也就是在计算的过程中将数据分配给每一个线程，每一个线程分别处理前向与后向传播过程。每一次迭代完成后，所有的线程都必须终止。图4给出了系统跟踪MPP的控制框图，图5为算法的结构图。

图4 MPPT系统框图

图5 反向传播法神经网络法的结构图

下面具体介绍利用BP神经网络法的操作步骤:

设网络的输入向量为Pk=(a1，a2，…，an);网络的目标向量为 Tk=(y1，y2，…，yq);中间层各单元的输入向量为 Sk=(s1，s2，…，sp)，输出向量为Bk=(b1，b2，…，bp);输出层各单元的输入向量为Lk=(l1，l2，…，lq)，输出向量为 Ck=(c1，c2，…，cq);输入层至中间层的连接权值为Wir(i=1，2，…n;r=1，2，…，p);中间层至输出层的连接权值为 Vrg(r=1，2，…，p，g=1，2，…，q);中间层单元输出阈值为θr(r=1，2，…，p);输出层单元阈值为γg(g=1，2，…，q)。

1)对 Wir，Vrg，θr，γg分别赋予(－1，1)的随机值。

2)选取输入样本和目标样本

3)计算中间层输入sr为

利用传递函数求中间层输出br为

4)计算输出层输入Lg为

利用传递函数求输出层输出为

5)根据目标值和实际的输出计算输出层各神经元的一般化误差为

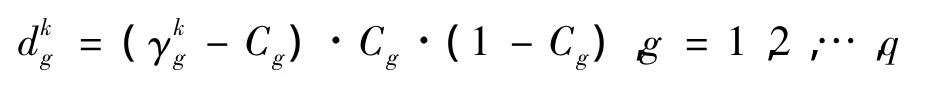
6)根据Vrg，计算中间层各单元的一般化误差为

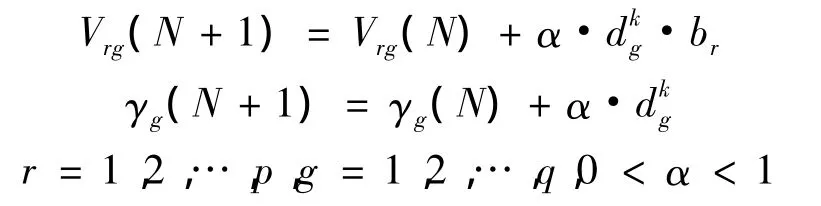
9)选取下一组学习样木，返回步骤3)重复训练，直到m组样本全部训练完成。如果网络的全局误差E小于预先设定的某个极小值，则网络收敛。如果学习次数大于预先的设定值且全局误差大于该极小值，则网络无法收敛。

10)学习结束。

由于BP算法是一种基于最速下降梯度法的算法，有容易陷入局部极值、收敛速度慢的缺点，从而使BP算法的时间过长，学习过程中容易陷入局部极值，因此，这就给网络训练增加了一定的困难。

通过对神经网络和灰色系统的研究，发现两者在信息的表现上具有一定的相似性。神经网络的输入对于系统而言，其输出可以以某一个精度去逼近一个固定的值，但是由于误差的存在，会使输出以某一个固定的值为中心上下波动，按照灰色系统中灰数的定义，可以认为神经网络的输出实际上就是一个灰数，由此可知，神经网络理论实际上包含了灰色系统的相关理论。

本文在预测的过程中，分别采用了传统的BP神经网络法及通过灰色理论改进的BP神经网络法，并对两种方法进行了对比。灰色系统的模型GM(m，n)是以灰色模块概念为基础，以微分拟合法为核心的建模方法。模型参数中m为模型微分方程的阶数，n为参与建模的序列个数。在上面的BP神经网络步骤的基础上，结合灰色预测理论，形成的预测算法为:

设时间序列x(0)={x(0)(1)，x(0)(2)，…，x(0)(n)}，利用 GM(1，1)模型可得到模拟{^x(0)(i)}(i=1，2，…n)，定义T时刻模拟值和真实值之差为时刻T的误差，即e(0)(T)=x(0)(T)－^x(0)(T)，建立误差序列 {e(0)(i)}(i=1，2，…，n)的BP神经网络。如果预测阶数为m，则利用{e(0)(i－j)}来预测i时刻的误差值，同时将{e(0)(i－j)}(j=1，2，…，m)作为BP神经网络的m个输入样本，e0(i)作为期望值，利用训练好的BP神经网络，预测出误差序列 ^e(0)(i)(i=1，2，…，n)。在此基础上计算新的误差值

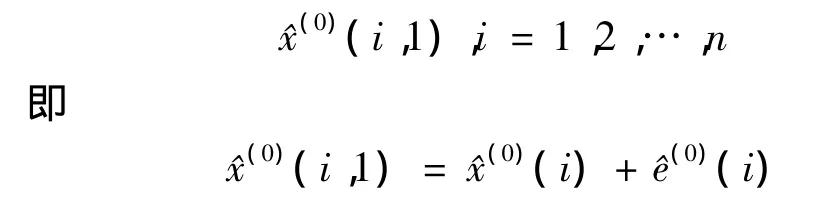
图6 预测功率误差曲线

3 计算结果

对提出的预测方法进行了计算［6－9］。实验所用的光伏电池的参数如表1所示，用本文方法所得计算结果以及误差如图6所示。计算结果表明，该算法可以在某一给定的温度和光照情况下，计算出PV系统在取得MPP时的输出电压和输出电流，这里记为Vmax，Imax。当温度、光照强度连续变化时，所求得的输出电流Imax、电压Vmax也随之变化。图4所示的脉冲发生器，可以从PV阵列中提取出系统的Vmax与Imax，通过Vmax与Imax来判断DC/DC变换器的脉冲切换频率，从而保证系统工作在MPP上。经过仿真计算可以看出，基于灰色BP神经网络算法的MPPT控制器在温度与光照强度迅速变化的情况下表现出良好的准确性和较快的计算速度。计算结果还同传统的BP神经网络法作了对比，图7为在温度和光照变化的情况下基于灰色BP神经网络的MPPT控制器的工作曲线，图8为利用灰色BP神经网络预测功率与传统的BP神经网络法预测功率的误差百分比作对比得出的误差曲线图。从图8中可以看出，除个别点(天气原因)外，灰色BP神经网络的预测误差百分比小于传统的BP神经网络。

表1 光伏电池参数表

图7 基于神经网络的MPPT控制器的工作曲线

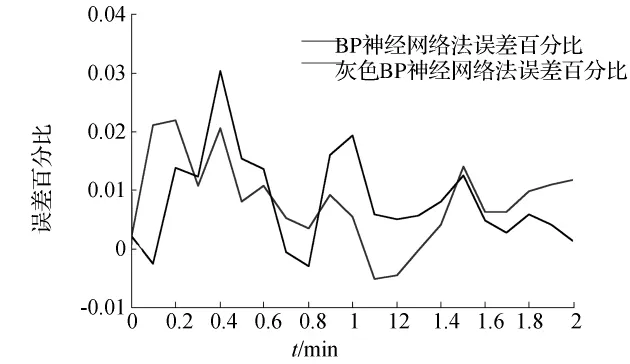
图8 两种方法的误差百分比曲线

4 结论

1)基于灰色BP神经网络的光伏发电系统的最大功率点跟踪方法，发挥灰色预测方法中“累加生成”的优点，能够削弱原始数据序列中的随机性并增强规律性，生成具有单调增长规律的累加序列便于BP神经网络进行训练。

2)本文算法避免了灰色预测方法及其预测模型存在的理论误差，且算法过程较为简单，容易实现。

3)由于与灰色理论相结合，本文算法使MPPT的计算精度有所提高，跟踪速度也相应加快，因此在温度与光照迅速变化的情况下能够迅速、准确地跟踪到系统的最大功率点。

［1］赵争鸣，刘建政，孙晓瑛.太阳能光伏发电及其应用［M］.北京:科学出版社，2005:20 －45.

［2］MESSENGER R，VENTRE J.Photovoltaic system engineering［M］.Florida:CRC Press，2005:963－973.

［3］ESRAM T，CHAPMAN P L.Comparison of photovoltaic array maximum power point tracking techniques［J］.IEEE Transactions on Energy Conversion，2007，439 －449.

［4］王松.一种基于神经网络的光伏电源最大功率控制系统［J］.电工技术学报，2004(4):45－48.

［5］郭亮，陈维荣，贾俊波，等.基于粒子群算法的BP神经网络光伏电池建模［J］.电工电能新技术，2011，30(2):84 －87.

［6］REVANKAR P S，GANDHARE W Z.Maximum power point tracking for PV systems using MATLAB/Simulink［C］∥2nd International Conference on Machine Learning and Computing.IEEE，2010:8－11.

［7］CHUN W N，ZUO S，YUKITA K，et al.Research on PV model and MPPT methods in Matlab［C］∥Asia Pacific Power and Energy Engineering Conferences.2010:1 －4.

［8］闻新.MATLAB神经网络应用设计［M］.北京:科学出版社，2001:35－72.

［9］邓聚龙.灰色系统基本方法［M］.武汉:华中理工大学出版社，1987:11－25.