三级配混凝土静动态弯拉强度尺寸效应试验研究★

张 建 金 龙 丁 宁

(1.江苏铭城建筑设计院有限公司，江苏盐城 224005;2.河海大学土木与交通学院，江苏南京 210098)

我国目前在大坝混凝土设计技术要求和施工质量检测中涉及的混凝土有关特性，几乎都是通过湿筛混凝土试件的试验结果来确定，因此研究湿筛混凝土动态力学特性具有重要的意义。目前国内外对湿筛混凝土动态力学特性的研究还很少，本文采用某拱坝实际工程材料及配比研究大坝混凝土静动态力学特性。现有动态试验揭示混凝土材料强度具有率敏感特性，随着应变率的提高而提高［1］。但有关混凝土材料动态强度的尺寸效应研究，试验数据非常有限，近期人们才将注意力转移到这一领域［2］。

通过将试验与相关尺寸效应理论结合，对不同尺寸(试件尺寸为450 mm×450 mm×1 700 mm和300 mm×300 mm×1 100 mm)的三级配混凝土梁的静/动强度的尺寸效应进行了试验研究，重点对相关尺度律理论在混凝土动态强度尺寸效应中的应用进行比较分析，具有重要的工程应用价值。

1 尺寸效应律

1.1 Weibull尺寸效应律

该理论假定结构内部缺陷的分布是均匀的，这样随着结构体积的增大，其破坏概率也增大。Weibull［3］认为，试件的破坏概率如式(1)所示，试件强度的分布服从负指数分布。

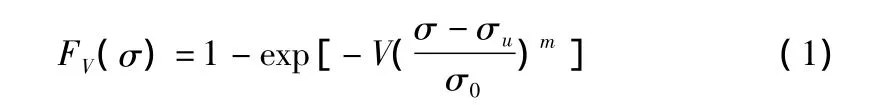
其中，m为Weibull模量;σu为临界强度值，常取值0;σ0为尺度参数。

1.2 Carpinteri的多重分形尺度律(MFSL)

非匀质材料的无序性对力学性能的影响取决于材料最大缺陷的尺寸与试件几何尺寸的比值。基于这个观点，A.Carpinteri［4］提出了多重分形尺度律(MFSL)，如式(2)所示:

其中，α为材料常数;D为材料的特征长度，对于弯拉试验来说，特征长度为其深度，mm。

在该尺度律中，认为材料自身结构对尺寸效应的影响最大。与Bazant尺度律相反，Carpinteri的多重分形尺度律更适用于无缺口试件，当试件尺寸无穷大时，该尺度律得到的强度还是有一残余值，这与实际情况较符合。

2 试验方案

2.1 配合比

试验结合大岗山高拱坝实际工程，除了水之外浇筑材料均从当地运至实验室，浇筑材料和配比都与大岗山实际工程一致。具体混凝土配合比如表1所示。

表1 三级配混凝土配合比

2.2 加载方案

为了研究不同尺寸对三级配混凝土静/动态弯拉特性的影响，采用尺寸为300 mm×300 mm×1 100 mm试件共6件和450 mm×450 mm×1 700 mm试件共4件，试件龄期为228 d。

2.3 试验方法

混凝土试件静动态试验采用简支梁三分点加载法，参照DL/T 5150-2001水工混凝土试验规程［5］自行设计了试验装置。本文就是文献［6］所采用的静动态弯拉试验技术，根据MTS作动器加载端部和试件的尺寸，重新设计加工了加压头和夹具支座。

静态加载速率为250 N/s，动态加载分别采用冲击波加载。

3 试验结果

3.1 试件破坏现象

试件在静动态弯拉试验中均在纯弯段断裂。典型的试件破坏见图1。

图1 试件破坏图

观察试件断裂面，发现不论是静态还是动态破坏试件，断裂面上粗骨料的断裂明显。而且，动态加载破坏试件断面上骨料断裂多，静态加载破坏试件断面上骨料断裂少，但界面破坏多。

3.2 混凝土静动态弯拉强度

根据实测的极限荷载值并结合试件的截面尺寸可以求得试件的弯拉强度。

试验结果表明:1)三级配混凝土动态弯拉强度均比静态强度高;2)大尺寸三级配混凝土均比小尺寸三级配混凝土的静动态弯拉强度低，具有明显的强度尺寸效应;3)大尺寸三级配混凝土均比小尺寸三级配混凝土的弯拉强度提高率低，说明加载率和加载时间对强度尺寸效应存在影响。

4 尺寸效应分析

由于本文是对光滑(无切口)试件进行静动态弯拉强度的尺寸效应分析，故选择Weibull尺度律与Carpinteri的多重分形尺度律进行相关的尺寸效应分析。

4.1 基于Weibull理论的尺寸效应分析

三级配混凝土试件纯弯段受拉区的体积的计算公式见式(3)。

其中，D为试件的深度，mm;试验采用的300 mm×300 mm×1 100 mm三级配混凝土试件纯弯段受拉区的体积为1.35×107mm3，450 mm×450 mm×1 700 mm三级配混凝土试件纯弯段受拉区的体积为4.556 25×107mm3。

绘制体积—静态弯拉强度对数图，拟合直线方程见式(4)。

其中，ftms为不同尺寸的试件静态弯拉强度，MPa;V为弯拉试件纯弯段受拉区的体积，mm3。

由上式可以得出静态参数 σs0=15.61 MPa，ms=11.11。

绘制体积—动态弯拉强度对数图，见图2。拟合直线方程见式(5)。

图2 动态弯拉强度和体积对数图

其中，ftmd为不同尺寸的试件动态弯拉强度，MPa;V为弯拉试件纯弯段受拉区的体积，mm3。

由上式可以得出动态参数 σd0=29.08 MPa，md=8.5。

动强度提高因子DIF定义见式(6)。

将式(5)和式(6)代入式(7)，就可以得到加载率对动强度提高因子DIF的尺寸效应，见式(10)。

受骨料尺寸的影响，对于三级配混凝土弯拉试件，其试件宽度规范规定为不小于300 mm，由图2可见，随着试件尺寸的增加，动弯拉强度提高因子DIF在减少，但减少程度还需要进一步的试验研究。

4.2 基于Carpinteri的多重分形尺度律(MFSL)的尺寸效应分析

300 mm立方体的标准抗压强度fc′=41.70 MPa，其抗拉强度ft′=2.77 MPa，试件所用骨料的最大粒径dmax=80 mm。结合静动态试验数据代入式(5)，则得到静动态弯拉强度与试件深度D(mm)的关系式，见式(11)与式(12)。

则动态强度提高因子DIF与试件深度D(mm)关系式为:

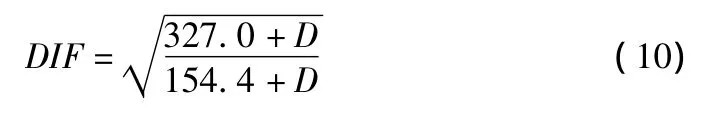
基于Weibull尺度律的静动态弯拉强度与试件深度D的关系式如下:

基于Weibull尺度律的动态强度提高因子与试件深度D的关系式如下:

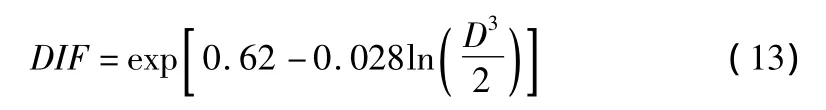
基于两种尺度律的静态强度与试件深度D的关系绘制成曲线，如图3所示。动态强度与试件深度D的关系如图4所示。动态强度提高因子DIF与试件深度D的关系如图5所示。

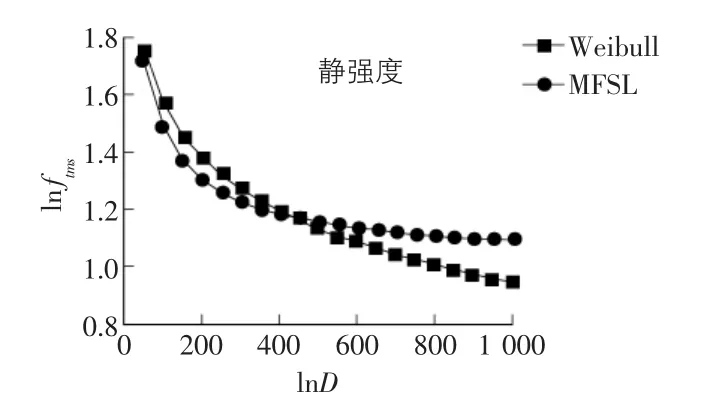
图3 静态弯拉强度和试件深度D（mm）的对数图

图4 动态弯拉强度和试件深度D（mm）的对数图

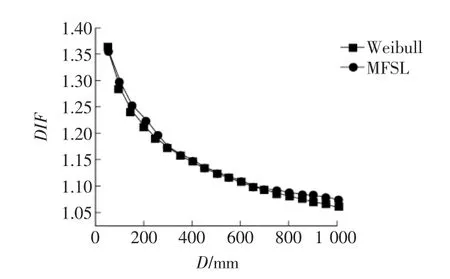
图5 动态强度提高因子DIF随试件深度D（mm）的变化图

从上述的对比曲线图可以看出，Weibull尺度律和MFSL均可用于三级配混凝土静动态弯拉强度的尺寸效应分析。但对于较大尺寸试件来说，MFSL的预测结果要稍好于Weibull理论。与静态弯拉强度的尺寸效应比较，动态弯拉强度的尺寸效应更为明显。

5 结语

根据本文对不同尺寸的三级配混凝土梁试件的试验结果及相应的分析，可以得到如下结论:

1)与众多研究者的试验结果类似，三级配混凝土的强度也随着加载速率(应变率)的提高而提高。2)三级配混凝土静动态弯拉强度均有显著的尺寸效应。与静态弯拉强度的尺寸效应比较，动态弯拉强度的尺寸效应更为明显。3)试件越大，相应的动态强度提高因子越小。4)Weibull尺度律和多重分形尺度律均可用于分析三级配混凝土静动态强度的尺寸效应。应用Weibull尺度律可以计算出三级配混凝土静动态弯拉强度标准值。对于较大尺寸试件来说，MFSL的预测结果要稍好于Weibull理论。

［1］ 周继凯，吴胜兴，沈德建，等.小湾拱坝三级配混凝土动态弯拉力学特性试验研究［J］.水利学报，2009，40(9):1105-1108.

［2］ Bazant Z P，Gettu R.Rate effects and load relaxation in static fractrue of concrete［J］.ACI Material Journal，1992，89(5):456-468.

［3］ Bazant Z P，Yunping Xi，Stuart G Reld.Statistical size effect in quasi-brittle structures:Ⅰ，Is Weibull theroy applicate［J］.Journal of Engineering Mechanics，ASCE，1991，117(11):2609-2622.

［4］ Alberto Carpinteri，Ferro G.Size effects on tensile fracture properties:a unified explanation based on disorder and fractality of concrete microstructure［J］.Materials and Structures，1994，27(10):563-571.

［5］ DL/T 5150-2001，水工混凝土试验规程［S］.

［6］ 吴胜兴，周继凯，沈德建，等.混凝土动态弯拉试验技术与数据处理方法［J］.水利学报，2009，40(5):569-575.