基于各向异性非结构网格的超声速流动自适应计算

邹建锋，盛 东，邢 菲，张 帅，杨永健

（浙江大学 玉泉校区航空航天学院，浙江 杭州 310027）

0 引 言

对于具有各向异性特征的流场，采用各向异性网格自适应技术，将会很大程度的降低计算量和提高流场结构的捕捉精度。各向异性网格自适应算法包含两方面的内容，即度量张量的离散定义和基于度量张量的网格生成。文献［1－8］等对各向异性网格的创建技术以及度量张量的离散定义方法做了广泛的研究和实践；文献［9－10］则将各向异性自适应技术应用于计算具有强间断的多介质界面流动问题，并对计算的可靠性和准确性做了对比研究。国内已有的相关研究主要关注各向异性网格的自动生成工作［11－12］。

超声速楔形体绕流及超声速横向喷流问题是高超声速飞行器流动控制及超燃冲压发动机燃料喷射等实际问题中的典型流动模式，具有显著的各向异性特征。如果能将各向异性网格自适应求解技术应用于这一类问题的研究，则对于深入分析高速流动问题有着很大的推动作用。本文的第1小节将对我们采用的各向异性网格自适应技术进行简要的介绍。第2小节给出了基于密度的可压缩N－S方程的求解方法。第3和第4小节是本文的主要部分，给出了各向异性自适应算法应用于超声速楔形体绕流及超声速横向喷流问题计算的收敛性和准确性分析。第5小节是全文的小结。

1 各向异性网格自适应技术

基于各向异性非结构网格的自适应求解技术在国内外相关文献中有着广泛的研究。本文主要参照文献［13－14］中的算法介绍，开展各向异性网格生成技术与自适应求解过程的实现；主要研究定常流动问题，对应的自适应迭代求解过程描述如下。（注：自适应求解之前，需要预先给定网格质量期望值q与网格单元期望数目N＊）

1）计算域初始网格系统创建

应用基于阵面推进技术（AFT）的三角形网格生成程序，对计算域进行三角形网格划分Tk（k＝0），得到初始网格系统。

2）流场解获取

应用本文第2小节介绍的可压缩问题求解器，获得Tk（k≥0）网格上的流场解φk。

3）度量张量矩阵计算

基于流场解φk，获得描述流场误差信息的Hessian矩阵Hk及其对应的度量张量矩阵Mk，其数学表达式如下：

其中，｜Δ｜和p（Δ）分别是网格单元的面积与周长，h＊＝h＊（N＊）是计算域网格单元的平均尺寸，所有几何测度都是在度量空间Mk内进行。函数Ft（0≤F≤1）是极值点在t＝1处的凸函数。网格系统的质量Qk定义为质量最差的网格单元质量值。

5）基于度量矩阵的网格重划分

对计算域执行新的三角划分Tk＋1，以获得在度量张量Mk定义的几何空间内为最优的三角化系统，并返回第2步。

其中，φk是流场物理量的第k次迭代解，λi与V分别是Hessian矩阵Hk的特征值与特征矢量。本文应用了基于Mach数场的度量张量矩阵。

4）网格系统质量判断

网格系统质量达到预定值q，则自适应循环结束。各向异性非结构网格系统的质量定义建立在度量张量Mk所定义的几何空间之上。本文采用的单元质量定义式为：

2 可压缩流动求解技术

需要提及的是，应用各向异性网格系统不需要专门的流体力学求解器。本文采用的是作者所在研究小组开发的并行流动及燃烧求解器，它建立在格点型非结构网格系统上，采用有限元形式的高阶低耗散格式。

3 高速楔形体绕流问题计算

美国国家应用软件研究中心CFD研究所（NPARC）的 CFD验证与确认网站［15］，提供了高速楔形体绕流问题（Ma＝2．5）的 Wind软件计算结果。本文对该问题进行了各向异性网格自适应求解，以验证该方法对高速流动问题的适应性和优越性。

图1展示了自适应求解过程中网格与马赫数分布情况的演变与收敛历程。初始网格的单元数为4866，节点数为2582。自适应计算中，网格单元数N＊被设置为2000。

由图1可以看出，自适应求解的第一次迭代就产生显著的效果，网格资源明显向激波附近汇集，计算得到的激波变得尖锐。经过四次迭代，自适应求解过程趋于收敛，网格单元被有效分配至激波附近的狭窄区域。

图2和图3给出了楔形体绕流自适应求解过程中马赫数分布曲线的演变及其与分析解［16］和 Wind软件数值解［15］的对比情况。Wind软件在计算中设计了155×101的结构网格系统。本文设计的各向异性网格系统的单元数为2000，约为Wind软件采用的网格数目的13%，网格规模有了大幅度的降低。

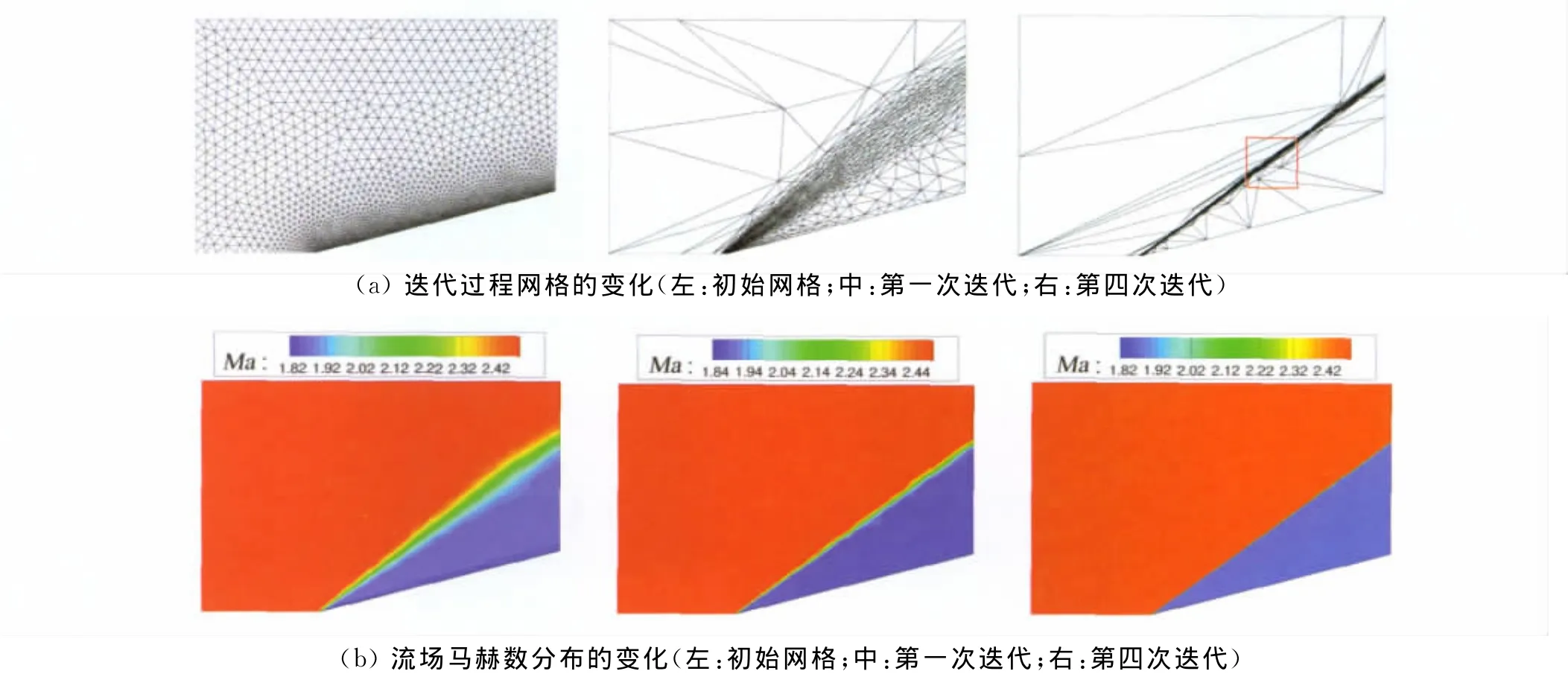
图1 楔形体绕流问题的自适应求解过程Fig．1 Adaptive solution for supersonic flow around a wedge

图2 楔形体绕流自适应求解过程马赫数分布曲线Fig．2 Mach number along free－stream direction

图3 马赫数分布曲线的局部放大特征Fig．3 Zoom in on the flow around shock wave

可以看出，波前马赫数在自适应迭代中与分析解吻合的很好。经过第三次迭代，波后马赫数与分析解达到一致，捕捉到的激波区域宽度与Wind软件基本一致。第四次迭代后，激波区域宽度进一步变窄并趋于收敛。Wind软件的计算结果在激波附近出现了明显的数值振荡，而在各向异性网格自适应求解中，数值振荡被有效减弱。

表1是本文计算结果与理论分析解及Wind软件模拟结果的定量对比。可以看出，本文的计算结果不但在定性上能捕捉到相对更加尖锐的激波效应，与理论分析解的定量对比也吻合的很好，物理量误差值与Wind软件模拟结果相比有了明显的下降。

表1 激波前后流场数据对比Table 1 Comparison of the present results with theory and Wind code

4 高速横向喷流干扰问题计算

为了研究各向异性非结构网格自适应算法在更加复杂的高速流动问题中的应用，我们计算了超声速横向喷流问题。

我们模拟的是声速射流横向喷入超声速来流所形成的复杂流动结构。超声速空气来流压力为3145Pa，来流马赫数为3．5。横向喷口位于超声速来流进口下游228．6mm处的位置，喷口尺寸为0．2667mm，射流压力与空气来流压力之比为8．74。

本文创建的各向同性网格系统包含165226个三角形单元，合计84280个节点。而各向异性网格自适应求解过程，我们把计算网格系统的单元规模N＊限定为5000。

图4给出了自适应求解过程中不同网格对应的净质量流率的收敛曲线。可以看出，在各向同性网格系统上，即初始网格，净流率的收敛速度较为缓慢，迭代4000余次净质量流率达到5．0×10－4的量级；而对于各向异性网格系统，迭代1000次后就能达到收敛，而且净质量流率为1．0×10－6的量级。

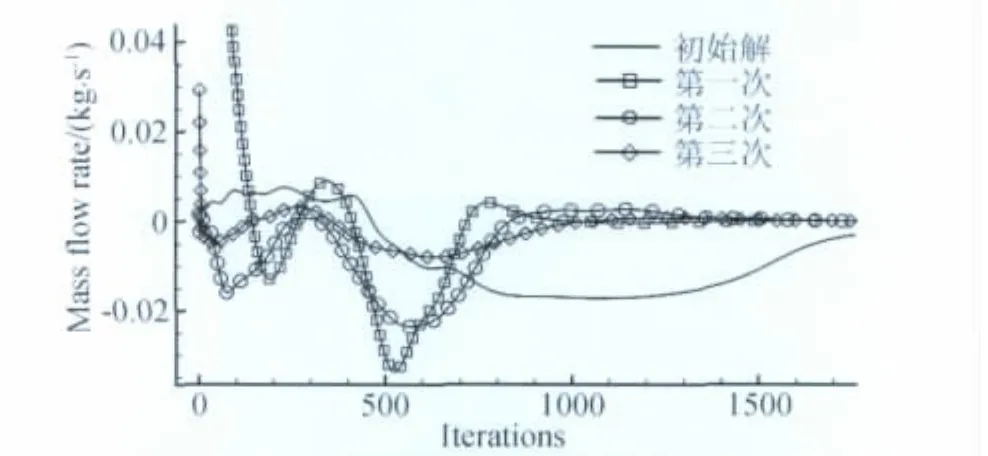
图4 不同网格系统上的收敛曲线对比Fig．4 Mass flow rate vs．adaption process

图5 是四次自适应计算过程后得到的网格系统及喷口附近流动情况。可以发现，在自适应过程中，计算区域的网格分布逐渐向激波间断等大梯度的局部区域集中，从而极大的提升了大梯度区域流场结构的分辨率。因此，各向异性网格自适应技术具有对有限的网格节点资源进行合理有效布置的功能。

图5 自适应求解得到的网格与马赫数分布Fig．5 Adaptive solution mesh and flow features

然而从图5可以发现，湍流边界层附近的流场没能被准确模拟和识别。也就是说，纯粹基于Mach数场的度量张量矩阵，不能有效定义和描述边界层内网格单元的尺寸分布及形状朝向。因此，对基于Mach数场的度量张量矩阵进行合理的改进使之能准确有效模拟边界层内的流动，这是对超声速横向喷流问题及其他更加复杂的高速流动问题进行各向异性网格自适应求解需要解决的关键技术难点。

5 存在的问题和进一步工作

本文对基于Hessian度量张量矩阵的各向异性非结构网格的创建，以及对基于各向异性非结构网格的自适应求解算法的实现，做了详细的介绍。并通过对高速楔形体绕流问题和高速横向喷流问题的自适应计算，展现各向异性非结构网格技术在准确模拟激波流场方面的独特优势以及存在的困难和问题。

本文研究表明，基于各向异性非结构网格的自适应求解具有如下几个方面的优点：

1）具有对网格单元资源进行合理的分配和布置的能力，有效降低问题的规模；

2）提升大梯度流动区域的计算分辨率；

3）有效降低激波附近流场的数值振荡；

4）提升激波前后流场物理量的计算精度；

5）具有良好的收敛性和收敛精度。

但在对高速横向喷流问题的计算中我们也发现，纯粹基于Mach数分布场的度量矩阵，不能准确描述湍流边界层内部的流动信息，尤其是对横向喷口附近的局部小涡结构以及激波／边界层的相互作用区域缺乏准确模拟的能力。因此，还需要对原有的度量张量矩阵进行合理的局部修改和完善，以满足上述流场特性的捕捉和计算。

［1］ HABASHI W，DOMPIERRE J，BOURGAULT Y．Anisotropic mesh adaptation：towards user－independent，mesh－independent and solver－independent CFD［J］．International Journal for Numerical Methods in Fluids，2000，32（6）：725－744．

［2］ DOMPIERRE J，VALLET M，BOURGAULT Y．Anisotropic mesh adaptation：towards user－independent，mesh－independent and solver－independent CFD［J］．International Journal for Numerical Methods in Fluids，2002，39（8）：675－702．

［3］ TAM A，AIT－ALI－YAHIA D，ROBICHAUD M．Anisotropic mesh adaptation for 3Dflows on structured and unstructured grids［J］．Computer Methods in Applied Mechanics and Engineering，2000，189（4）：1205－1230．

［4］ DOLEJSI V．Anisotropic mesh adaption technique for viscous flow simulationp［J］．East West Journal of Numerical Mathematics，2001，9（1）：1－24．

［5］ BOTTASSO C．Anisotropic mesh adaption by metricdriven optimization［J］．International Journal for Numeri－cal Methods in Engineering，2004，60（3）：597－639．

［6］ DOLEJSI V，FELCMAN J．Anisotropic mesh adaptation for numerical solution of boundary value problems［J］．Numerical Methods for Partial Differential E－quations，2004，20（4）：576－608．

［7］ FREY P，ALAUZET F．Anisotropic mesh adaptation for CFD computations［J］．Computer Methods in Applied Mechanics and Engineering，2005，194（48－49）：5068－5082．

［8］ REMACLE J，LI X，SHEPHARD M．Anisotropic adaptive simulation of transient flows using discontinuous Galerkin methods［J］．International Journal for Numerical Methods in Engineering，2005，62（7）：899－923．

［9］ BELHAMADIA Y，FORTIN A，CHAMBERLAND E．Anisotropic mesh adaptation for the solution of the Stefan problem［J］．Journal of Computational Physics，2004，194（1）：233－255．

［10］BELHAMADIA Y，FORTIN A，CHARNBERLAND E．Three－dimensional anisotropic mesh adaptation for phase change problems［J］．Journal of Computational Physics，2004，201（2）：753－770．

［11］徐明海，陶文铨．二维各向异性非结构化网格的自动生成与应用［J］．西安交通大学学报，2002，3（3）：222－235．

［12］赵建军，钟毅芳，周济．各向异性网格生成及其在曲面三角化中的应用［J］．中国图像图形学报，2002，7（9）：950－955．

［13］VASSILEVSKI Y，DYADECHKO V，LIPNIKOV K．Hessian－based anisotropic mesh adaptation in domains with discrete boundaries［J］．Russian Journal of Numerical Analysis and Mathematical Modelling，2005，20（4）：391－402．

［14］LIPNIKOV K，VASSILEVSKI Y．Analysis of Hessian recovery methods for generating adaptive meshes［R］．In：IMR．Los Alamos National Laboratory Institute of Numerical Mathematics，2006，163－171．

［15］http：／／www．grc．nasa．gov／WWW／wind／valid／archive［EB］．html．

［16］ANDERSON J．Modern compressible flow［M］．New York：McGraw Hill Inc，1982．