基于绝热加速量热方法的危险化学品的热危险性评定及统计分级方法
2013-08-20刘宏
刘 宏
中国人民武装警察部队学院基础部,河北廊坊 065000
0 引言

在获得这些数据后,可以对这些危险化学品的危险性有一个了解,还有一个任务就是要对这些危险品的危险性进行分级。以往人们多采用聚类分析的方法进行分级。这种方法的缺点在于把各项指标的重要性看作一样重要,其效果可想而知了。也有采用统计综合评价方法,这种方法是把一项指标线性的映射到〔0,100〕。这和实际的情况有较大的出入。还有其它的分类方法,比如非线模糊处理方法等。本文采用降半正态分布、升半正态分布对各项指标进行标准化处理,然后对各项指标的重要性进行排序,采用降半正态分布得到各项指标的权重,最后采用统计方法对危险化学品进行分级。
1 各项指标的标准化处理

f(x)的函数值随x 的增大而减少。
f(x)的函数值随x 的增大而增大。
对于初始放热温度T0(℃),把样本的数据从小到大进行排序,最小值为28.48 度,最大值为411.4 度,中值为246.14 度。由于初始放热温度T0(℃)其值越小越危险,所以采用降半正态分布。把28.48 所对应的危险性设为1,246.14 所对应的危险性设为0.5, 411.4 所对应的危险性设为0.1,通过解方程得到对应函数:

其图像如下图所示:

图1 初始放热温度T0(℃)标准化函数图像
同理可以得到最高温升速率温度、最高温升速率时间的对应函数。

其图像如下图所示:

图2 最大温升速率标准化函数图像
同理可以得到绝热温升、最高放热温度、初始放热温升速率的对应关系。
2 各个危险性因素标准化

让最重要因素的比重设为1,第3 个的比重设为0.5,第7个的权重设为0.1。可以解得权重函数:
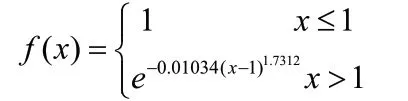
即比重值分别为:1, 0.901, 0.709, 0.499, 0.319, 0.186, 0.099.
把它们归一化后为:0.269,0.243,0.191,0.135,0.086,0.050,0.027.
3 采用统计方法进行分级

4 本文方法的优点
本文方法的优点体现在四个方面。一是对各个指标的量化。聚类分析把每一个危险化学品的各个指标数值看成是同等重要的,而实际情况是初始放热温度T0(℃)的重要性是最大的,它代表危险化学品开始反应的温度。统计综合评价方法是把一项指标线性的映射到〔0,100〕,这和实际情况有很大的出入。比如初始放热温度T0(℃)的最小值是28.48℃,最大值为411.4℃。把28.48℃的危险性设为1,200℃的危险性为0.552.在平时生活的环境中,28.48℃是很容易达到的温度,而200℃相应的就比较难达到。用本文的量化方法,200℃的危险性为0.2195.这一数值更合理一些。
二是对其余的危险化学品进行实验后,所得的结果可以代入到相应的对应函数中,得到该危险化学品的危险性数值。比如初始放热温度T0(℃)的数值小于28.48℃时,它的危险性为1;初始放热温度T0(℃)大于411.4℃时,也可以代入公式得到它的危险性。
三是实验的指标增多时,本文的方法具有可扩展性、简单易用性。文献[4]给出的指标体系有五项:初始放热温度、最大功密度、绝热反应温升、热自燃温度、沸点。本文给出的指标体系有七项。如果用层次分析法构造判断矩阵,那是一个比较麻烦的工作,并且还需要进行一致性检验。当指标的多少变更时,需要重新进行构造判断矩阵及一致性检验的工作。在对指标的重要性排序后,用降半正态分布给出各指标的权重,具有可扩展性、简单易用性的特点。
四是把危险化学品分为五类符合人们的认知规律。本文的分类结果是中等危险的危险化学品占比最大,其次是较高危险的危险化学品和中等危险的危险化学品,占比最小的是高危险的危险化学品和低危险的危险化学品。经本专业的专家对分类结果的鉴别,认为分级比较合理,有很好的实用价值。
[1]冯长根,傅智敏,等.绝热方法评价热安定性的改进模型与应用.北京理工大学学报,2003,2:23-25.
[2]杨春笋,等.化学品危险性鉴别分类研究的现状与展望.中国安全科学学报,2009,3: 67-70.
[3]李荣平,李剑玲.多指标统计综合评价方法研究.河北科技大学学报:2004,68:85-87.
[4]顾静.典型危险化学品反应危险性分级与预防措施研究.青岛科技大学,2010,6.
