多次区间载荷下结构混合动态可靠性的计算*

方永锋 陈建军 阎彬 曹鸿钧

(西安电子科技大学 电子装备结构设计教育部重点实验室，陕西 西安 710071)

有时结构在其服役期承受的载荷和其强度都具有不确定性.随机分析和模糊分析是目前结构工程中处理不确定性问题时应用最为普遍的两种方法［1-5］，但不论是随机分析还是模糊分析都对已知信息有较强的依赖性.然而在实际工程中，往往可得到的数据贫乏，不足以确定不确定参数的概率分布函数或模糊隶属度函数，且可靠度的预测结果对分布参数的准确性较为敏感，分布参数很小的误差有时可能导致可靠度计算结果呈现较大的误差［6］，这在很大程度上限制了随机和模糊的方法在工程中的应用.为此，文献［7-8］认为，当掌握的不确定性参数信息较少时，则宜采用区间或凸集模型来描述问题的不确定性.文献［9-10］提出了基于区间分析的结构非概率可靠性模型，并预测了区间静载荷作用一次或特定次数时结构的可靠度.实际上在结构服役期内，随机型和区间型不确定因素往往是共同存在的，对于同时含有随机变量和区间变量的结构可靠性问题，利用混合模型获得结构的可靠度，似比给出一确定的单值具有更高的可信度［11］.文献［12］提出了结构的随机-区间问题的顺序单回路法(SSLM)处理方法，但只考虑了静力学问题.文献［13］从理论上证明了区间变量转化为随机变量与直接计算随机-区间变量对于结构可靠度的计算结果是相同的.文献［14-15］利用区间因子研究了随机-区间结构系统的静力学可靠性问题，得到的结构可靠度是一个常量.然而，由于振动、冲击、疲劳、腐蚀、老化等外在因素以及一些不确定性内在因素的共同影响，结构的可靠性往往是与时间有关的函数.文献［16］给出了一种考虑载荷服从某种概率分布且多次作用下零件的可靠性预测模型，但该模型在实际应用时，当作用荷载等幅的条件难以满足时，导致其可靠性的预测结果误差偏大且难以避免.文献［17-19］对结构的动力可靠性问题进行了分析，但仅限于作用载荷为平稳随机过程的情况.许多情况下，结构在服役过程中受到的载荷既不是一次也不是仅一种，往往是多次与多种.

文中基于对结构动态概率可靠性研究的基础，针对实际问题中掌握作用载荷的统计信息量较少的情况，利用随机-区间理论，对结构承受的多次区间载荷随时间变化的情况进行了分析.根据应力-强度干涉理论，建立了当作用载荷随时间变化且结构强度随时间退化时结构的动态随机-区间可靠性预测模型，并对模型中的区间参数进行随机化处理，利用一次二阶矩法获得结构的动态可靠性指标和可靠度.最后通过两个算例说明了文中预测模型的合理性、实用性和精确性.

1 动态载荷与动态强度

1.1 动态载荷

作用于结构上的载荷为任意的时变载荷，且载荷的幅值为区间变量，为了求得在此种情况下结构在任意t 时刻的可靠度，文中对结构承受的载荷作如下处理:

(4)令ΦsI(t)=max{Φ(t)}，ΦsI(t)对应的区间记为sI(t)，将sI(t)称为载荷作用多次时的最大区间应力，它对应的应力即为最大区间应力.

若结构在最大区间载荷下不失效，则结构在这多次区间载荷下也不会失效.故区间载荷作用多次时的结构可靠度等价于这些载荷中最大区间载荷的可靠度.

记

sI(t)的均值与离差分别为

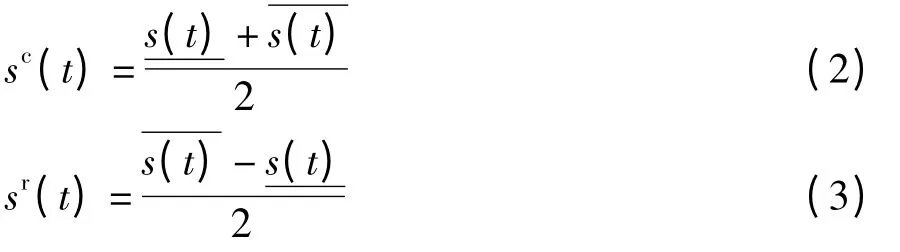
1.2 动态强度

考虑结构的强度为随机变量，在结构服役期内，由于振动、冲击、疲劳、腐蚀、老化等外在因素以及一些不确定性内在因素的共同影响，导致结构的强度是随时间退化的.文献［20］认为可用weibull 分布来描述剩余强度，而且给出了结构在t 时刻的剩余强度为

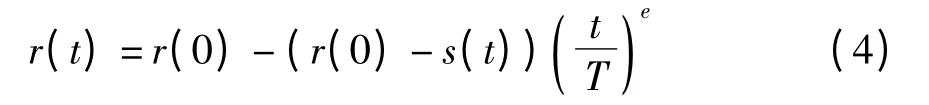
式中，r(0)是结构的初始强度，s(t)是结构的动态应力，T 是结构的生命周期，e 是材料的退化指数.

根据式(4)和weibull 分布的性质，可得到结构在t 时刻的剩余强度的均值为

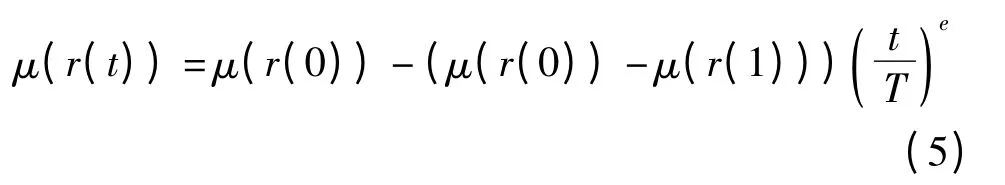
式中，μ(r(0))为结构的初始强度的均值，μ(r(1))=μ(s(t))，为结构服役期末的强度的均值.

结构剩余强度的均方差为

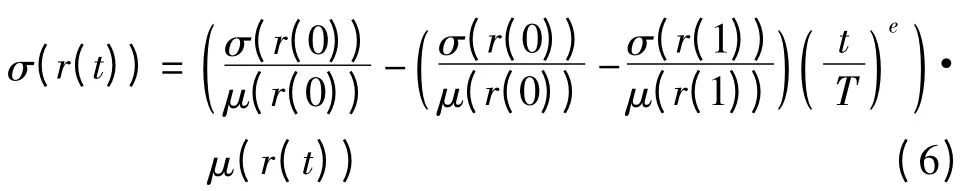
式中，σ(r(0))为结构的初始强度的均方差，σ(r(1))为结构服役期末的强度的均方差.

2 结构的区间-随机动态可靠性分析

文献［13］从理论上证明了如下结论:对于只含有区间变量与随机变量的可靠性问题，把区间变量转化为均匀分布的随机变量，就把区间-随机可靠性问题转化为传统的随机可靠性问题，用一次二阶矩法计算可知，两者的可靠度结果是等价的.

基于上述结论，可将式(1)对于结构的可靠度计算转化为

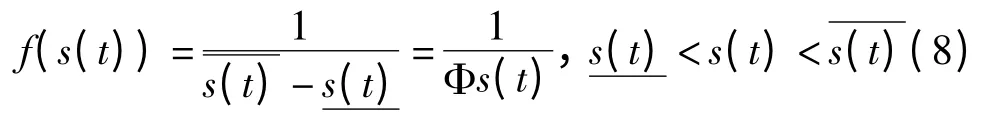
由式(8)可得s(t)的均值和方差分别为

再根据应力-强度干涉理论，则可得到在多次区间载荷作用下且结构强度退化时的功能函数为

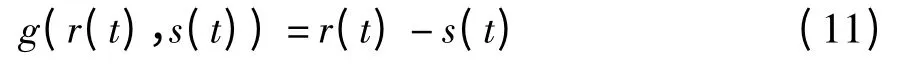
为了保证用一次二阶矩法计算可靠度的精确性，将s(t)和r(t)在任意t 时刻当量标准正态化处理为(X(t)，Y(t))，如此可求得结构的动态可靠性指标为

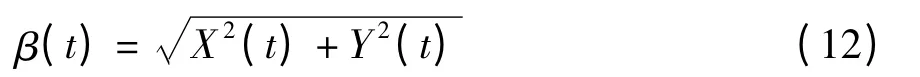
初始值由(10)得到，经过反复迭代计算式(12)，可得任意t 时刻的结构动态可靠性指标为与(X*(t)，Y*(t))相对应的(r(t)，s(t))即为式(11)的最大失效点.

在迭代过程中，为了加速收敛，根据经典响应面法的迭代选点方法，则在第k+1 迭代过程中有

这里a 第一次取2.25，以后各次迭代取0.75［18］，

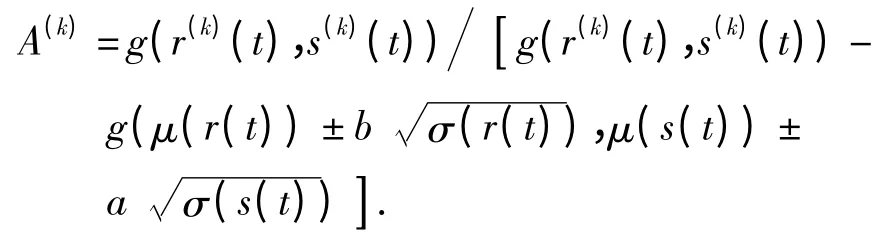
对于r(t)，若服从正态分布则直接计算，否则采用下式:

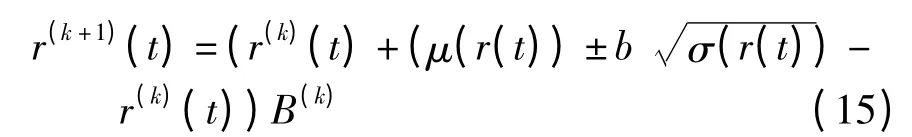
这里b 第1 次取3，以后各次迭代取1［19］，r(0)(t)=μ(r(t))

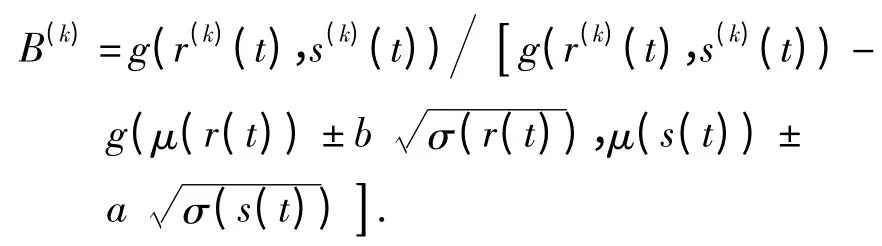
当满足:

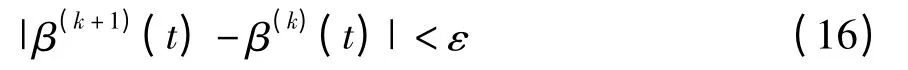
时迭代终止.式中，β(k+1)(t)、β(k)(t)分别为第k +1次和第k 次可靠性指标，ε 为迭代终止要求的精度.

综上，给出多次区间载荷作用下且结构随机强度退化时结构动态随机-区间可靠度的算法如下:

(1)由2.1 求区间载荷的等价区间应力;

(2)由式(7)将区间应力转化为均匀分布的随机应力;

(3)把上一步转化的随机应力与随机强度当量标准正态化;

(4)应用一次二阶矩法计算可靠性指标β(1)(t);

(5)用式(14)、(15)计算可靠性指标β(k+1)(t);

(6)计算式(16);

(7)若前一步达到了收敛精度，计算终止，否则继续由步骤(5)进行迭代，直至满足收敛精度，迭代终止，输出β(*)(t)，并据β(*)(t)值由标准正态概率分布函数表获得结构的动态可靠度.

3 算例

例1 某汽车后轴在不考虑强度退化的情况下，其强度r(0)服从均值为160 MPa、均方差为15 MPa的正态分布.由2.1 可得到载荷的工作应力s(t)的范围为45～115 MPa，在载荷作用多次时，用文中方法得到的和利用SSLM 及蒙塔卡罗方法(MCM)模拟106次计算得到的可靠度结果见表1.

表1 例1 3 种方法计算结果比较Table 1 Comparison of computation results of example 1 by using three methods

从表1 可以看出，SSLM 和文中方法的计算结果误差相当，且与MCM 的计算结果基本一致，但文中方法的迭代次数要比SSLM 几乎少一半，表明该方法的敛速快、精度高.

例2 某车体底座，其强度r(t)随时间退化，其初始强度r(0)服从均值为150 MPa、均方差为15 MPa的正态分布，T=10000h，e=4.092.由2.1 可得到载荷的工作应力s(t)的范围为45～115MPa，在载荷作用多次且考虑强度退化时，利用文中方法和MCM模拟计算106次在时间t=0，500，1500，5000，9000 h时的结构动态可靠度，结果见表2.

表2 例2 不同时刻两种方法计算结果比较Table 2 Comparison of computation results of example 2 by using two methods

从表2 中可以看出，文中提出的方法与MCM两者的计算结果几乎一致;在考虑结构强度退化时，结构在多次区间载荷作用下的可靠度是随时间持续下降的.该结果可为结构生命的全周期检测与动态设计提供参考依据.

例3 某悬臂管结构如图1 所示，受到外力F1(t)、F2(t)、P(t)和扭矩W(t)的共同作用.图中，d 为悬臂管的外直径，ι 为悬臂管的厚度，L1为悬臂管的长度，L2为F2的力臂长度.给定T=10000 h，e =4.092.该结构中各个不确定参数的取值见表3，对随机变量，则分布参数1 和2 分别表示均值与均方差，对区间变量，则分布参数1 和2 分别表示区间变量的下界和上界.若该结构可靠，则施加于管端面的等效应力smax(t)应小于结构的强度r(t)，对应的极限状态方程为

g(r(t)，s(t))=r(t)-smax(t).

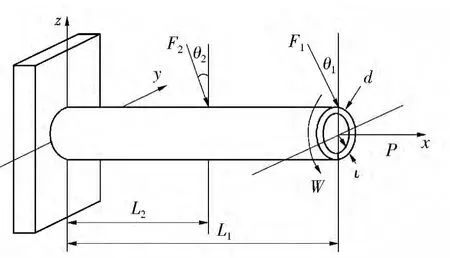
图1 某悬臂管Fig.1 A cantilever tube

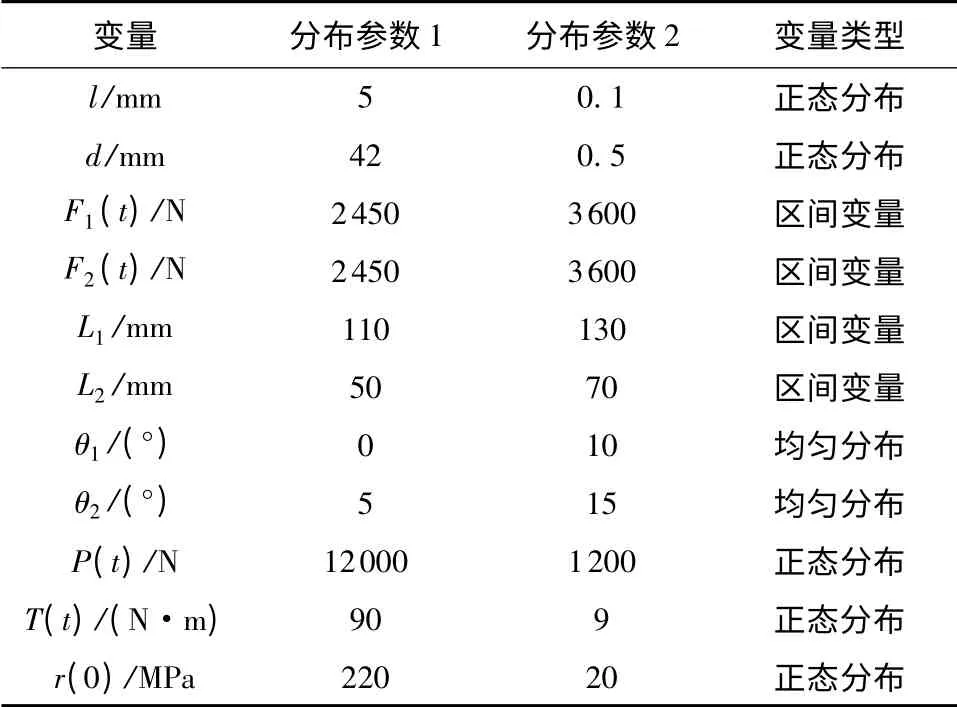
表3 悬臂管不确定参数Table 3 Uncertain variables for the cantilever tube

其中，

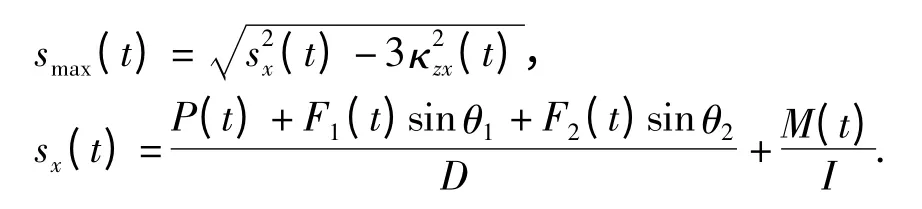
式中，θ1、θ2分别是F1、F2与z 轴的夹角，D 为截面积，计算公式为

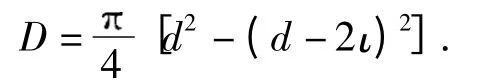
M(t)为弯矩，计算公式如下

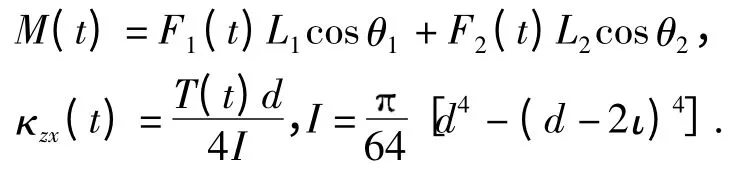
本算例在t=0 时刻，也就是不考虑强度退化的时候，仅考虑一次载荷作用下，文献［13］用SSLM 方法，迭代次数16 次，计算可靠度为0.971 6，文中方法迭代6 次即可达到该结果.在考虑强度退化时，多次载荷作用时文中方法与MCM 模拟106在不同时刻的计算结果见表4.

从表4 中可以看出，文中方法与MCM 在0、500、1500、5000、9000 h 时两者的计算结果基本相同，但迭代次数明显要少.同时也说明，在考虑强度退化，外部作用多次时悬臂管的可靠度是随时间不断下降的.

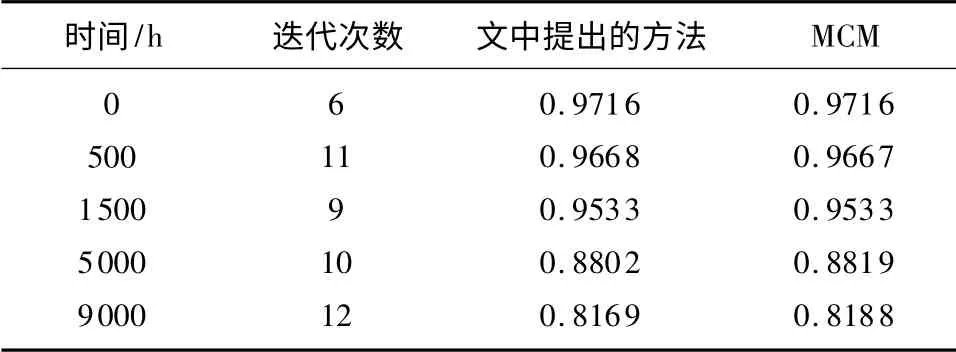
表4 例3 不同时刻两种方法计算结果比较Table 4 Comparison of computation results of example 3 by using two methods

4 结论

文中针对多次区间载荷作用、且结构随机强度退化的情况构建了结构动态可靠性预测模型，经过理论推理和算例验证得到如下的结论:

(1)针对实际问题中掌握作用载荷的统计信息量较少的情况，利用随机-区间理论，对结构承受的多次区间载荷随时间的变化情况进行了分析和等效处理;

(2)建立了当作用区间载荷随时间变化且结构随机强度随时间退化时结构的动态随机-区间混合可靠性预测模型，并对模型中的区间参数进行随机化处理，利用一次二阶矩法得到了结构的动态可靠度.最后通过3 个算例说明了文中模型的合理性、易行性与实用性.

［1］Ditlevsen O，Madsen H O.Structural reliability methods［M］.Chichester:Wiley，1996:135-158.

［2］Madsen H O.First order vs.second order reliability analysis of series structures ［J］.Structures Safety，1985，2(3):207-214.

［3］Madsen H O，Krenk S，Lind N C.Methods of structural safety［M］.Englewood Cliffs:Prentice-Hall，1986:59-78.

［4］Ayyub B M，Lai K L.Structural reliability assessment with ambiguity and vagueness in failure［J］.Naval Engineering Journal，1992，104(3):21-35.

［5］Jiang Qimi，Chen Chun Hsien.A numerical algorithm of fuzzy reliability ［J］.Reliability Engineering ＆ System Safety，2003，80(3):299-307.

［6］Ellishkoff I.Essay on uncertainties in elastic and viscoelastic structures:form A M Freudenthal's criticisms to modern convex modeling ［J］.Computers ＆ Structures，1995，56(6):871-895.

［7］Ben-Haim Y.A non-probabilistic concept of reliability［J］.Structural Safety，1994，14(4):227-245.

［8］Ben-Haim Y，Elishakoff I.Discussion on:a non-probabilistic concept of reliability［J］.Structural Safety，1995，17(3):195-199.

［9］邱志平.非概率集合理论凸方法及其应用［M］.北京:国防工业出版社，2005:23-37.

［10］郭书祥，吕震宙，冯元生.基于区间分析的结构非概率可靠性模型［J］.计算力学学报，2001，18(1):56-60.Guo Shu-xiang，Lu Zhen-zhou，Feng Yuan-sheng.A nonprobabilistic model of structural reliability based on interval analysis ［J］.Chinese Journal of Computational Mechanics，2001，18(1):56-60.

［11］朱增青，陈建军，梁震涛，等.随机-区间型天线结构有限元及可靠性分析［J］.高技术通讯，2008，16(6):624-629.Zhu Zeng-qing，Chen Jian-jun，Liang Zhen-tao，et al.Finite element and reliability analyses for antenna structures with the mixture of random and interval variables［J］.Chinese High Technology Letters，2008，16(6):624-629.

［12］Du Xiao-ping，Agus Sudjianto，Huang Bei-qing.Reliability-based design with the mixture of random and interval variables［J］.Journal of Mechanical Design，2005，127(12):1068-1077.

［13］Jiang C，Lu G Y，Han X，et al.A new reliability analysis method for uncertain structures with random and interval variables［J］.International Journal of Machine Material Design，2012，6(8):169-182.

［14］Gao W.Interval finite element analysis using interval factor method ［J］.Computational Mechanics，2007，39(4):709-717.

［15］Gao Wei.Natural frequency and mode shape analysis of structures with uncertainty［J］.Mechanical Systems and Signal Processing，2007，21(1):24-39.

［16］王正，谢里阳，李兵.考虑载荷作用次数的零部件可靠性模型［J］.机械强度，2008，33(1):68-71.Wang Zheng，Xie Li-yang.Li Bing.Reliability model of component considering tomes of random load acting［J］.Journal of Mechanical Strength，2008，30(1):68-71.

［17］胡太彬，陈建军，高伟，等.平稳随机激励下随机桁架结构动力可靠性分析［J］.力学学报，2004，36(2):241-246.Hu Tai-bin，Chen Jian-jun，Gao Wei，et al.Dynamic reliability analysis of stochastic truss structures under stationary random excitation［J］.Acta Mechanica Sinica，2004，36(2):241-246.

［18］赵俊钊，陈务军，潘钦，等.梁柱结构协同作用的车辐式索杆体系成形分析［J］.华南理工大学学报:自然科学版，2011，39(12):152-158.Zhao Jun-zhao，Chen Wu-jun，Pan Qin，et al.Analysis of formation of spoke-shaped cable-strut system with synergistic effect of column-beam structures ［J］.Journal of South China University of Technology:Natural Science Edition，2011，39(12):152-158.

［19］韩大建，宋雄彬，王海涛.带弹性支撑杆张拉结构整体找形分析的动力松弛法［J］.华南理工大学学报:自然科学版，2005，33(11):66-71.Han Da-jian，Song Xiong-bin，Wang Hai-tao.Dynamic relaxation for integer form-finding analysis of tension structures with elastic supporting bars ［J］.Journal of South China University of Technology:Natural Science Edition，2005，33(11):66-71.

［20］Schaff J R，Davidson B D.Life prediction methodology for composite structures，Part I-constant amplitude and two-stress level fatigue［J］.Journal of Composite Materials，1997，31(2):128-157.