随机参数激励下齿轮系统的分岔与稳定性*

王靖岳 郭立新 王浩天

(1.东北大学 机械工程与自动化学院，辽宁 沈阳 110819;2.沈阳航空航天大学，辽宁 沈阳 110136)

长期以来，人们对齿轮传动系统的非线性动力学研究取得了丰富的成果［1-8］.但是，制造、安装过程中的随机因素，材料特性的随机性，外界随机因素和物理、几何参数的随机性等等，都会造成齿轮传动系统的动力学特性具有随机性.因此，国内外专家学者开始注意到随机因素对齿轮传动系统的影响，对齿轮传动系统随机非线性特性进行了深入的研究，文献［9］建立一个齿轮非线性随机动力状态空间模型，利用它来预测系统的剩余使用年限.文献［10］建立考虑速度相关的随机误差的齿轮传动系统随机振动模型，借助开发的仿真系统，研究随机误差对振动加速度的影响.文献［11］建立含间隙和时变啮合刚度的齿轮系统，并分析了系统在随机外激励因素作用下的全局动力学特性.文献［12］考虑非白噪声误差，建立了齿轮随机振动建模，通过此模型来验证随机误差对振动加速度的影响.文献［13］建立二自由度齿轮传动系统非线性动力学模型，利用蒙特卡洛法对其在参数随机激励下参数的随机扰动对系统动力学行为的影响.

文中在文献［14］的研究基础上，考虑齿轮阻尼比、齿侧间隙、啮合频率、啮合刚度和输入力矩的随机扰动，建立一个单对三自由度的直齿轮副的随机振动模型，分析系统随齿轮啮合频率变化的分岔特性、稳定性及其随机扰动对系统动力学的影响.

1 系统的动力学模型

采用集中质量法建立了一个单对三自由度的直齿轮副的随机动力学模型，如图1 所示.

忽略传动轴的扭转和弯曲变形，仅考虑齿轮的扭转振动.图中，Fb1和Fb2为主、从动轴上轴承对齿轮的作用力;θg1和θg2为主、从动齿轮的扭转角位移;yg1和yg2为两齿轮中心的位移;e()为齿轮啮合综合误差，为时间;fb1和fb2为主、从动轴上轴承的位移函数;rg1和rg2为主、从动齿轮的基圆半径;ch为齿轮副的啮合阻尼系数;cb1和cb2为主、从动轴上轴承的阻尼系数;Tg1和Tg2为作用在主、被动齿轮上的转矩;fh为轮齿啮合的位移函数;mg1和mg2分别为主、从动齿轮的质量;kb1和kb2为主、从动轴上轴承的平均支撑刚度;Ig1和Ig2为主、从动齿轮的转动惯量.

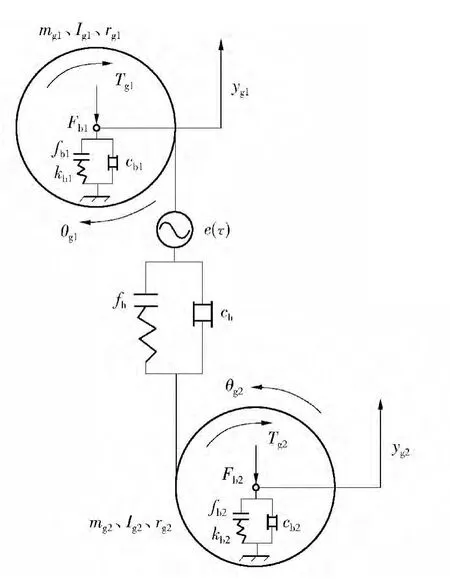
图1 齿轮系统的动力学模型Fig.1 Dynamic model of the gear system

忽略输出扭矩的波动，考虑因输入扭矩波动引起的低频外激励和静态传递误差e()引起的高频内部激励，则有

式中:Tg2()为输出扭矩;Tg2m为输出扭矩的平均值;Tg1()为输入扭矩;Tg1m为输入扭矩的平均值;Tg1a()为输入扭矩的变化部分.

齿轮副的基本参数见表1.

表1 齿轮基本参数Table 1 Parameters of the gear pair

对齿轮系统进行受力分析，根据牛顿定律可以得系统的运动学微分方程:

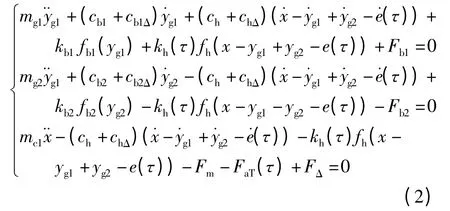
式中:“·”表示对时间的导数;x 为齿轮副的相对位移;chΔ为齿轮副的啮合阻尼的随机扰动量;cb1Δ和cb2Δ为主、从动轴上轴承的阻尼随机扰动量;mc1=Ig1Ig2/(Ig1rg22+Ig2rg12)，Fm=Tg1m/rg1=Tg2m/rg2，x =rg1θg1-rg2θg2，kh()=kh+2/(ωh+ωΔ))=khm+FaT()=mc1Tg1a()·rg1/2Ig1.其中:ωh为啮合频率;ωΔ为啮合频率的随机扰动量;kh()为齿轮啮合刚度，随时间周期变化;khm为平均啮合刚度系数;FΔ为输入力矩的随机扰动量;khar为各谐波分量系数，φhr为相位角(r =1，2，3，…，∞).假定齿轮啮合综合误差和输入扭矩的变化部分均为单频的简谐函数，即e()=easin((ωh+ωΔ)+φh)，FaT)=Fasin((ωt+ωtΔ) +φh)，ea为齿轮啮合综合误差系数;ωt为输入转矩的频率;ωtΔ为输入转矩频率的随机扰动量;φh和φt为其对应的初相位.齿轮传动的相对扭转位移为

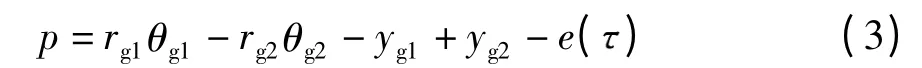
如图2 所示，齿轮副的间隙为2b，则无量纲间隙¯b=b/be，其中，be为给定的标称尺寸.

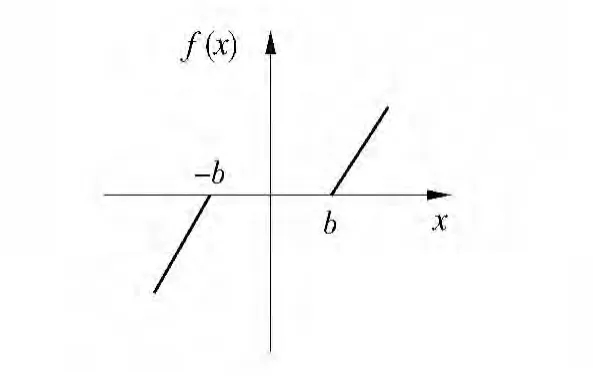
图2 齿侧间隙与力的关系图Fig.2 Relation between gear backlash and force diagram

［11］，对方程(2)进行无量纲化，令z1=则系统的状态方程组为

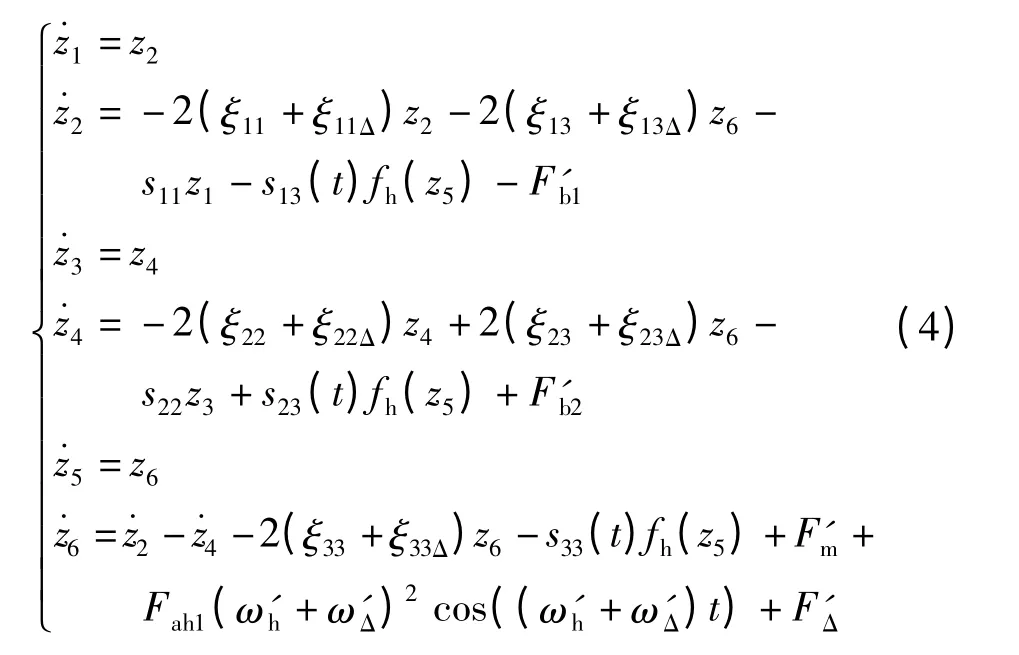
式中:无量纲阻尼比ξ11= cb1/(2mg1ωn)，ξ22= cb2/(2mg2ωn)，ξ13= ch/(2mg1ωn)，ξ23= ch/(2mg2ωn)，ξ33=ch/(2mc1ωn);F'b1和F'b2为主、从动轴上轴承对齿轮的无量纲作用力，且F'b1=Fb1/(mg1be)，F'b2=Fb2/(mg2be);s11=/，s13= mc1/m1，s22=/，s13(t)=s23(t)=s33(t)/4，s23=mc1/m2，s33(t)=1-(ε+εΔ)cos(ωht)，ε 为无量纲齿轮啮合刚度，ε =khar/khm，εΔ为无量纲齿轮啮合刚度随机扰动量;ξ11Δ、ξ13Δ、ξ22Δ、ξ23Δ和ξ33Δ为无量纲阻尼比随机扰动量，ξ33Δ=chΔ/(2mc1ωn)，ξ23Δ=chΔ/(2mg2ωn)，ξ22Δ=cb2Δ/(2mg2ωn)，ξ13Δ= chΔ/(2mg1ωn)，ξ11Δ= cb1Δ/(2mg1ωn);Fah1为齿轮啮合综合误差，Fah1=e/be;F'm为无量纲切向平均作用力，F'm=Fm/(mc1be);ω'h为无量纲啮合频率;F'Δ为无量纲输入力矩的随机扰动量，F'Δ=FΔ/(mc1be);ω'Δ为无量纲啮合频率的随机扰动量.齿轮啮合间隙非线性函数为

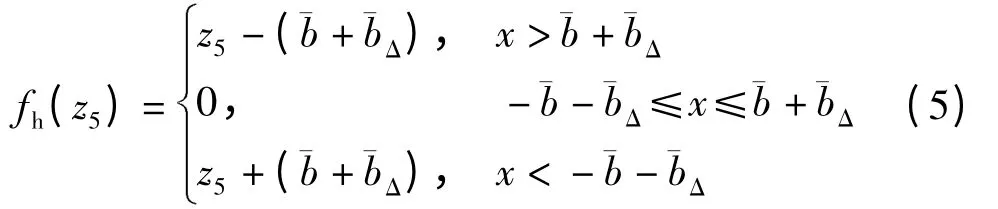
2 数值仿真分析

2.1 分岔与稳定性

所取系统参数如下:Fah1=0.05，ξ11= 0.01，ξ22=0.01，ξ13=0.012，ξ23=0.012，ξ33=0.05，=1.0，F'm=0.01，F'b1=0.2，F'b2=0.2，k11=1.3，k22=1.3，F'Δ服从N(0，0.0012)的正态分布，在(-0.004，0.004)范围内取值;ξ11Δ、ξ22Δ、ξ13Δ、ξ23Δ、ξ33Δ、Δ和εΔ服从N(0，0.0012)的正态分布，在(-0.04，0.04)范围内取值;ω'Δ服从N(0，0.0000052)的正态分布，在(-0.00002，0.000 02)范围内取值，随机量均满足3σ 理论.取初始状态x1(0)=0，x2(0)=-0.1，x3(0)=0，x4(0)=-0.1，x5(0)=0，x6(0)=-0.1，以啮合频率ω'h为分岔参数，令ω =，利用四阶龙格-库塔法对系统进行数值仿真，可得到系统啮合频率在(0.1，6.0)上的全局图，如图3 所示.随着啮合频率的减小，系统先是做周期1 运动，当ω=2.75 时，系统通过倍化分岔到周期2 运动;当ω =2.55 时，系统通过倍化分岔到周期4 运动，随着啮合频率的进一步减小，系统进入混沌运动;当ω =2.3 时，系统由混沌运动到周期1 运动;当ω =2.1 时，系统再次进入混沌运动;当ω =1.55 时，系统由混沌运动到周期1 运动;当ω =1.45 时，系统通过倍化分岔到周期2 运动，随着啮合频率的进一步减小，系统进入混沌运动;当ω =1.15 时，系统由混沌运动到周期1 运动;当ω=1.05 时，系统再次由周期1 运动进入混沌运动;当ω =0.37 时，系统由混沌运动到周期1 运动.

图3 系统的全局分岔图Fig.3 Bifurcation diagram of the system

设计合理的齿轮传动系统应具有较高的稳定性，稳定性包括运动状态稳定性［15］，即转速的小扰动不会引起系统运动状态的改变(分岔的发生);还有就是系统振动强度的稳定性［16］，即转速的小扰动不会引起振动幅值的突变.根据以上稳定性原则可以选取齿轮系统稳定运行区间，齿轮啮合频率应该避开的区间如下:

(1)从全局分岔图3 上可以看出:当啮合频率分别为2.75 和1.45 时系统发生分岔，该分岔点附近极易发生转速微扰而引起运动状态失稳，而运动状态的改变必然对应着较差的可靠性，因而选择转速时应该避开.

(2)从全局分岔图3 上可以看出:啮合频率在区间(0.37，1.05)、(1.15，1.35)、(1.55，2.10)和(2.30，2.45)上为混沌运动区间.因为混沌运动意味着不可预测性和永不重复性，它总是不停地从前一时刻的某周期轨道上突然到下一时刻的其他轨道上，而运动的不断变化会加剧齿轮系统的疲劳，因而选择转速时应该避开.

2.2 啮合频率的随机扰动对分岔的影响

为分析啮合频率的随机扰动对系统分岔的影响，取啮合频率在(2.2，3.0)上的局部分岔图，见图4.

从图4(a)-(d)中可以看出，随着啮合频率的减小，随机扰动的增大，系统发生分岔的时间点逐渐提前;有的已消失，直接进入混沌运动(见图4(d)).可见，啮合频率随机扰动的大小变化对系统的分岔特性影响很大，啮合频率随机扰动的微小变化即可影响系统的动力学特性.

图5 为不同啮合频率下的Poincaré 映射图.从图5(a)可以看出，系统作周期1 运动;随着啮合频率随机扰动的逐级增大，吸引子变得比以往更发散，但大部分被限制在原吸引子附近，仍作周期1 运动.图5(b)为不同形态的混沌吸引子，可以看出啮合频率随机扰动的逐级增大没有改变系统的混沌运动状态.

从图5(c)中可以看出，系统先作周期8 运动，随着啮合频率随机扰动的逐级增大，系统变为混沌运动.从图5(d)和5(e)中可以看出，系统先作周期4 和周期2 运动;随着啮合频率随机扰动的增大，ω 服从N(0，0.0000052)的正态分布时，系统仍作周期4 和周期2 运动;随着啮合频率随机扰动的进一步增大，ω 服从N(0，0.000 052)和N(0，0.000 52)的正态分布时，系统变为混沌运动，但混沌吸引子形态各不相同.

图4 系统的局部分岔图Fig.4 Local bifurcation diagram of the system

图5 系统的Poincaré 映射图Fig.5 Poincaré map of the system

取ω=2.68 时，从系统的时间历程曲线图6 和相图7 可以看出，随着啮合频率随机扰动的增大，系统从周期运动转向混沌运动.

图6 ω=2.68 时系统的时间历程曲线Fig.6 Time course diagram of the system when ω=2.68

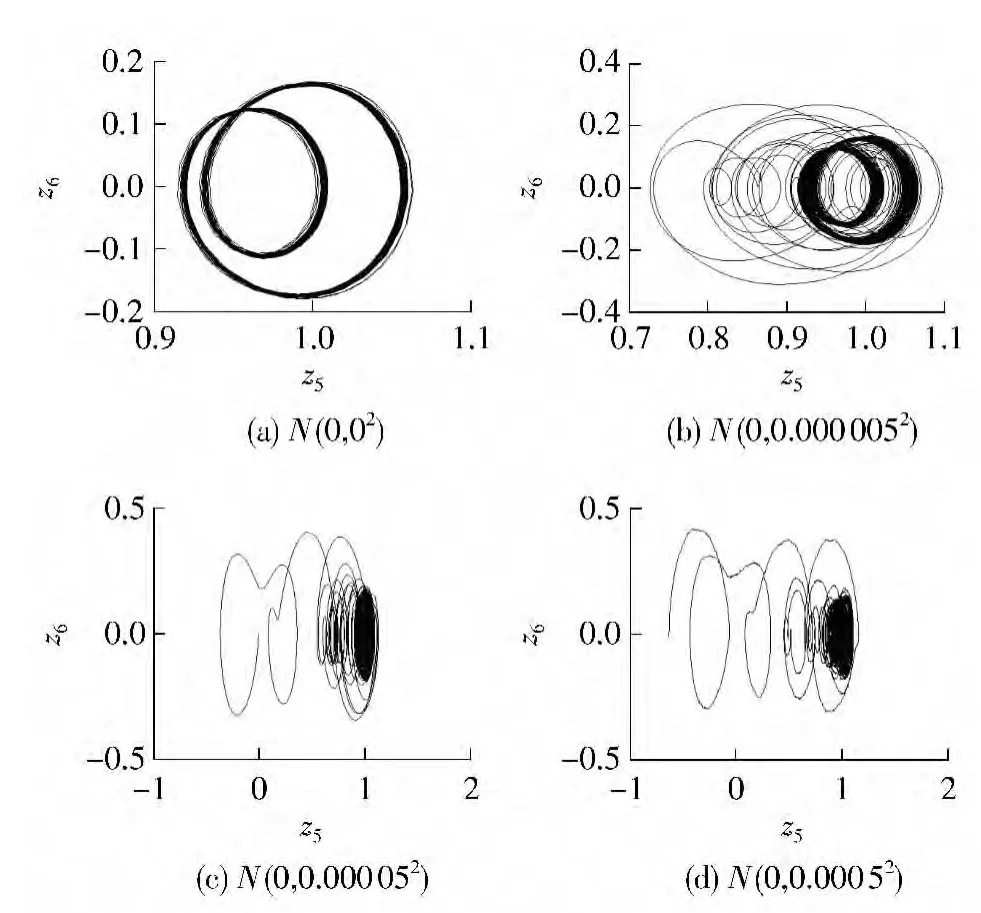
图7 ω=2.68 时系统的相图Fig.7 Phase diagram of the system when ω=2.68

3 结论

考虑输入力矩引起的低频外激励、齿轮阻尼比、齿侧间隙、啮合频率和啮合刚度的随机扰动等因素对系统动力学的影响建立了单对三自由度非光滑直齿齿轮系统的随机动力学模型和微分方程.利用四阶龙格-库塔法对齿轮系统的运动微分方程进行数值求解，用系统的Poincaré 映射图、相平面图、时间历程图和分岔图分析了系统在激振频率变化的情况下混沌的形成过程.随着啮合频率的减小，齿轮系统通过周期倍化分岔从周期运动转向混沌运动，再从混沌运动转向周期运动.通过剔除6 处不稳定转速区段，可获得无量纲啮合频率在(0.1，6.0)上的稳定速度区间.文中研究结果对工程中选择合理的齿轮转速有一定的参考价值.啮合频率的随机扰动对系统的动力学特性影响较大，随机扰动的微小变化即可改变系统的分岔特性，在建模时要考虑其大小的影响再决定取舍.

参考文献:

［1］Chen Z G，Shao Y M，Lim T C.Non-linear dynamic simulation of gear response under the idling condition［J］.International Journal of Automotive Technology，2012，13(4):541-552.

［2］Yang J M.Vibration analysis on multi-mesh gear-trains under combined deterministic and random excitations［J］.Mechanism and Machine Theory，2013，59:20-33.

［3］Yang J Y，Peng T，Lim T C.An enhanced multi-term harmonic balance solution for nonlinear period-one dynamic motions in right-angle gear pairs ［J］.Nonlinear Dynamics，2012，67(2):1053-1065.

［4］Chang-Jian C W.Bifurcation and chaos analysis of the porous squeeze film damper mounted gear-bearing system［J］.Computers ＆ Mathematics with Applications，2012，64(5):798-812.

［5］Wang J，Lim T C，Li M F.Dynamics of a hypoid gear pair considering the effects of time-varying mesh parameters and backlash nonlinearity［J］.Journal of Sound and Vibration，2007，308(1/2):302-329.

［6］Byrtus M，Zeman V.On modeling and vibration of gear drives influenced by nonlinear couplings［J］.Mechanism and Machine Theory，2011，46(3):375-397.

［7］Chang-Jian C W，Hsu H C.Chaotic responses on gear pair system equipped with journal bearings under turbulent flow［J］.Applied Mathematical Modelling，2012，36(6):2600-2613.

［8］Moradi H，Salarieh H.Analysis of nonlinear oscillations in spur gear pairs with approximated modelling of backlash nonlinearity［J］.Mechanism and Machine Theory，2012，51:14-31.

［9］Matej G，Dani J，Pavle B，et al.Model-based prognostics of gear health using stochastic dynamical models［J］.Mechanical Systems and Signal Processing，2011，25(2):537-548.

［10］Wang Y，Zhang W J.Stochastic vibration model of gear transmission systems considering speed-dependent random errors［J］.Nonlinear Dynamics，1998，17(2):187-203.

［11］刘梦军，沈允文，董海军.随机外激励下齿轮非线性系统的全局分析［J］.中国机械工程，2004，15(13):1182-1185.Liu Meng-jun，Shen Yun-wen，Dong Hai-jun.Global analysis for the nonlinear gear system with stochastic external external excitation ［J］.China Mechanical Engineering，2004，15(13):1182-1185.

［12］Wang Yong，Zhang Wen-jun.Modelling of gear stochastic vibration considering non-white noise errors ［J］.Chinese Science Bulletin，1999，44(4):375-378.

［13］卢剑伟，刘梦军，陈磊，等.随机参数下齿轮非线性动力学行为［J］.中国机械工程，2009，20(3):330-333.Lu Jian-wei，Liu Meng-jun，Chen Lei，et al.Nonlinear dynamics behavior of gear system with stochastic parameters［J］.China Mechanical Engineering，2009，20(3):330-333.

［14］Kahraman A，Singh R.Nonlinear dynamics of a geared rotor-bearing system with multiple clearances［J］.Journal of Sound and Vibration，1991，144(3):469-506.

［15］郜志英，沈允文，李素有，等.间隙非线性齿轮系统周期解结构及其稳定性研究［J］.机械工程学报，2004，40(5):17-22.Gao Zhi-ying，Shen Yun-wen，Li Su-you，et al.Research on the periodic solution structure and its stability of nonlinear gear system with clearance［J］.Chinese Journal of Mechanical Engineering，2004，40(5):17-22.

［16］陈安华，罗善明，王文明，等.齿轮系统动态传递误差和振动稳定性的数值研究［J］.机械工程学报，2004，40(4):21-25.Chen An-hua，Luo Shan-ming，Wang Wen-ming，et al.Numerical investigations on dynamic transmission error and stability of a geared rotor-bearing system［J］.Chinese Journal of Mechanical Engineering，2004，40(4):21-25.