水中悬跨结构动力特性试验与计算研究＊

雷 凡 杨吉新 邓育林

（武汉理工大学交通学院 武汉 430063）

0 引 言

水中结构特别是海洋结构经常受到波浪、海流和地震等外部荷载的作用产生振动，严重时可能产生疲劳破坏.以海底油气管道为例，我国已建成的石油天然气管道超过2 000km，每年的检测和维修费用高达几百万甚至几千万美元，由于结构损坏造成的停产损失更是无法估量［1－2］.因此水中结构的动力稳定性分析一直是科学工作者研究的重点与难点，水中结构的试验研究也显得尤为重要.

海底长输管线的悬跨段、海洋浮式结构物的系泊缆绳、水中悬浮隧道等结构属于水中悬跨结构，容易在波浪、海流等动力因素的影响下产生较大变形，引起结构的损伤甚至破坏.本文针对水中悬跨结构进行模型试验研究.分若干工况对各个模型在无水和有水环境下的动力特性进行测试，并分别采用附加质量法以及三维数值有限元法进行计算和分析，探讨水中悬跨结构动力特性特点.

1 水中悬跨结构模型试验

为研究水中悬跨结构的动力特性，设计制作了9组不同尺寸的悬跨结构模型，分别对其在空气与水中的动力特性进行测试.

1.1 试验模型与试验装置

1）试验模型 为准确把握水中悬跨结构的动力效应，研究水对结构动力特性的影响，专门制作了9个试验模型，模型试验结构选用Ⅰ级钢筋，规格分别为Φ10，Φ16，Φ22，每种钢筋分别取3种长度：1，2，4m.另外各取50cm用于材料试验，经测试，钢材的弹性模量为208GPa，泊松比为0.29，密度为7 845kg／m3.加工后的模型见图1.

图1 试验模型

2）试验装置 水槽：长6m，宽3m，高1.6 m，设有进水口及出水口，为方便观察试验进程，水槽一侧采用玻璃钢代替混凝土围墙，试验水槽见图2a）.

量测系统：采用安正CRAS振动及动态信号采集分析仪；TS24108电荷输出加速度传感器；安正CRAS振动及动态信号采集分析软件V7.0，见图2b）.

图2 试验装置

1.2 试验步骤

1）将仪器安装连接，在水池中的水泥块上安装支架（其上设有可调节距离的螺栓）.

2）根据试件长度调整2个水泥块的距离，并将试件两端用螺栓及钢丝固定在支架上.

3）在试件1／4，1／2，端点处布置测点，将加速度传感器置于测点上.设置CRAS振动及动态信号采集分析软件中的各项参数.

4）用力锤敲击试件，系统开始做自由振动，这时传感器识别出振动参量，经CRAS振动及动态信号采集分析软件处理，显示出其频谱图及波形图，经分析后即得出系统的振动频率.

5）重复上述步骤反复进行测量.

1.3 试验工况

试验有9个试件，分为3种规格3种长度，每个试件分别进行空气中与水中的动力测试，共18个工况.为准确比较空气中与水中结构的振动频率，测试同一试件在两种状态下的振动.

1.4 试验结果

经过反复测试，钢筋的振动频率结果较稳定，频谱分析结果见表1～3.

表1 1m长的钢筋在水中与空气中的试验结果

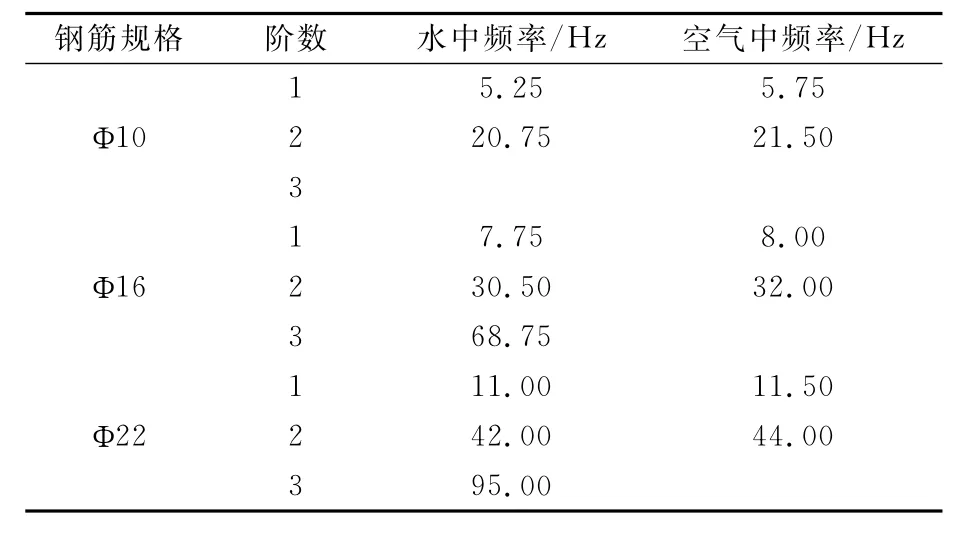
表2 2m长的钢筋在水中与空气中的试验结果

表3 4m长的钢筋在水中与空气中的试验结果

2 三维数值模拟

采用可实现流固耦合分析的三维实体单元和三维声学流体单元对试验模型进行离散.建模时，实体单元按照结构实际尺寸建立，由于流体范围远大于结构尺寸，可作为无限水域考虑，在此使用6倍于结构半径的水域代替流体范围［3－4］.结构与流体接触面采用 FSI（fluid－solid interaction）标记.

分别计算长度为1，2，4m，直径分别为10，16，22mm的钢筋在空气和水中的振动频率，计算结果见图3.

3 公式法

计算水中结构的固有频率时，使用附着在结构表面一定质量的水体来代替水的动力学效应，这种近似的算法称为附加质量法，即本节所指的公式法.这种方法假设水为无粘、无旋和不可压缩的理想流体，并假设水中结构为刚体.由于计算简便，附加质量法在工程界中的应用也十分广泛.

利用附加质量法求解问题的关键是附连水质量的计算，令总动能值与单位长度附连水质量的动能相等，可求出相当的附连水质量mf，圆柱体附连水质量可表示为［5－7］

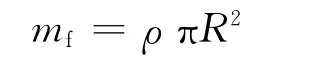
式中：ρ为流体密度；R为截面半径.

使用理论公式和附加质量法得到模型计算结果，见图3.

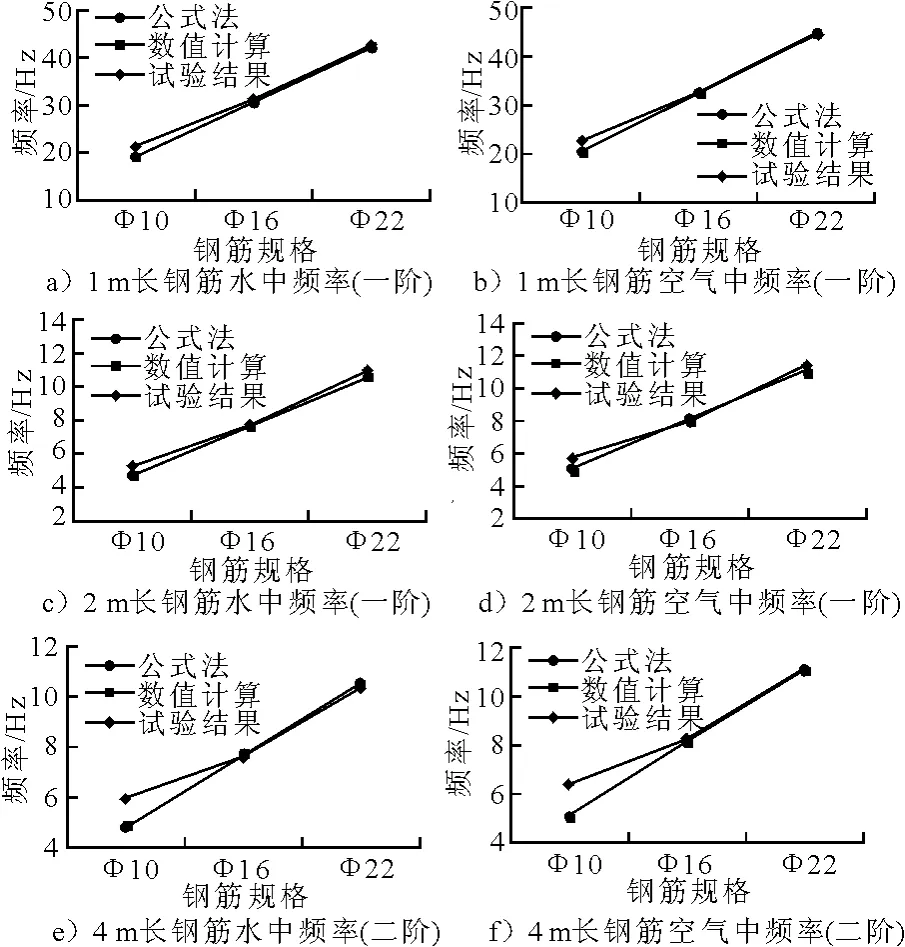
图3 计算结果比较

4 结果分析

由于试验条件、试件长度等因素的影响，部分试件的前三阶频率未完全识别出来，因此图3中分别取了1和2m长钢筋的一阶频率，以及4m长钢筋的二阶频率进行比较.

表4列出了试验所得频率与数值计算频率相对差值的百分率.

表4 试验结果与数值计算结果比较表 %

由图3和表4可以看出，随着钢筋直径的增加，三条曲线的变化趋势基本相同.其中，数值计算结果与公式法的计算结果非常接近，所有工况下，空气和水中的数值计算结果与公式法的计算结果的最大差值的百分率仅为1.3%和0.69%.试验结果与数值计算结果、公式法的计算结果也十分接近，长度分别为1，2，4m的Φ16和Φ22钢筋，其振动频率的试验结果与数值计算结果十分接近，相对差值的百分率均小于5%，仅Φ10钢筋振动频率的试验结果略大于其余二者，可能是由于试验过程中，Φ10钢筋两端的约束不佳所致.

为分析钢筋在空气和水中的振动特性差异性，取各工况下每根钢筋一阶频率的数值计算结果进行比较.同一规格钢筋在不同长度和不同介质条件下的频率变化曲线见图4.

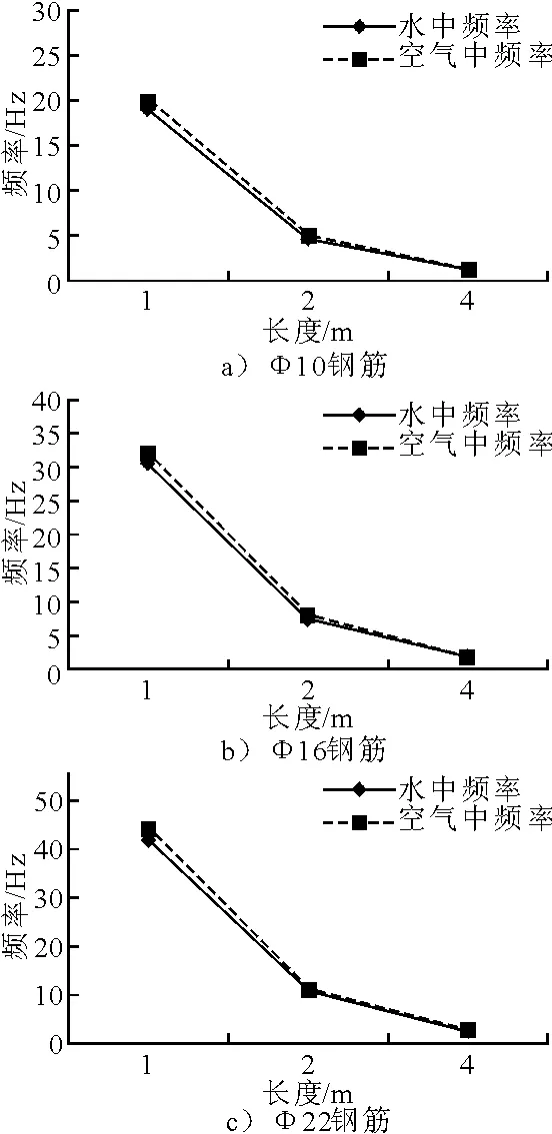
图4 空气与水中的一阶频率比较图

由图4可以看出，各种工况下，钢筋在空气中的一阶频率均大于其在水中的一阶频率，原因是结构在振动过程中，流体对于结构的作用相当于增加了结构自身的质量，使振动频率降低.3种规格下，不同长度钢筋在水中和在空气的振动频率相对差值的百分率比较接近，约为5%～6%.由于结构在水中与在空气中的振动频率不同，这将影响水中结构的动力响应，因此，为准确进行水下结构的动力分析，应考虑流固耦合效应.

5 结 论

分若干工况对水中悬跨结构模型在无水和有水环境下的动力特性进行了测试，根据模型试验的现象和试验数据，分析了不同尺寸、不同规格模型的动力特性.并采用附加质量法以及三维数值有限元法对试验模型动力特性进行了计算.试验及计算结果表明：水中结构动力特性测量具有一定难度，测量结果可能受温度、环境等因素的影响，也可能由于传感器放置位置、激励锤敲击方位、试验仪器本身的误差、试验模型约束条件等因素导致数据的误差；3种规格下，不同长度钢筋在水中和在空气的振动频率相对差值的百分率比较接近；水对结构的动力特性有一定影响，为准确进行水中结构的动力分析，应该考虑结构与水的相互作用.

［1］方华灿.油气长输管线的安全可靠性分析［M］.北京：石油工业出版社，2002.

［2］ROMAGNOLI R，VARVELLI R.An integrated seismic response analysis of offshore Pipeline－sea floor systems［C］∥7th International Conference on Offshore Mechanics and Arctic Engineering，1988：139－147.

［3］LEI Fan，YANG Jixin，XIE Xizhen.The numerical calculation research on dynamic characteristics of pipe conveying fluid［C］∥Recent Advances in Nonlinear Mechanics 2009，Kuala Lumpur：Springer Press，2009：72－73.

［4］LEI Fan，YANG Jixin，LIU Hui.Dynamic response analysis of deepwater pier with fluid－solid interaction［C］∥Guangzhou：Trans Tech Publications，2010：161－166.

［5］黄玉盈.液固耦联系统固有频率的一个变分式［J］.华中工学院学报，1985，13（1）：91－96.

［6］钱 勤，黄玉盈，刘忠族.求附连水质量的一种直接方法［J］.力学与实践，1996，18（5）：19－21.

［7］苏海东，黄玉盈.求半无限域流场中物体附连水质量的一种简便解法［J］.华中科技大学学报，2003（4）：14－16.