软硬岩互层边坡稳定性的敏感性因素分析＊

2013-08-18夏开宗陈从新鲁祖德宋娅芬周意超

武汉理工大学学报（交通科学与工程版） 2013年4期

夏开宗陈从新鲁祖德宋娅芬周意超

（中国科学院武汉岩土力学研究所岩土力学与工程国家重点试验室武汉 430071）

0 引言

软硬岩互层型边坡的地质灾害对国家建设和人民的生命财产安全构成了严重威胁.如侏罗系地层在长江三峡库区广泛出露，三峡工程库区移民迁建工程在建设过程中形成了大量的软硬岩互层型高陡边坡，边坡失稳事故时有发生.

软硬岩互层边坡作为一类具有典型特点的层状边坡，边坡在地质结构、破坏特征等方面不仅具有独特性，而且其稳定性影响因素与一般边坡具有很大的差异性，当地表水的浸入使岩层间软弱岩层强度降低或边坡前缘开挖形成临空面时，边坡上的岩、土体在水力作用触发下稳定性极差［1－3］.影响此种类型的边坡稳定性的因素是较多的，如层面强度、岩层厚度、岩层倾角、水力作用等，掌握这些因素对边坡稳定性影响规律，能为滑坡的处置技术和优化方法提供有针对性的依据.

本文依托沪蓉国道主干线湖北宜昌至巴东高速公路上多处软硬岩交互型边坡为背景，针对这些边坡的破坏特征，建立了边坡力学模型，分析了层面强度、岩层厚度、岩层倾角、水力作用等各项因素对边坡稳定性的影响，探索这些因素对软硬岩互层边坡稳定性影响的一些规律.

1 分析原理

1.1 边坡分析模型

通过对研究区沿线20多处软硬岩互层滑坡进行地质调查，如妃台山滑坡、鹰咀岩滑坡、周家坡滑坡、彭家湾路段古崩滑坡等，发现此种类型的边坡变形破坏不仅取决于软弱层面的力学性质，而且受边坡中地下水力作用的活动控制.因此，本次建立的边坡稳定性分析模型考虑了水力作用.在Hoek和Bray［4］给出的典型岩石边坡水力学模型的基础上，建立了适合研究区软硬岩互层边坡如下的分析力学模型见图1.

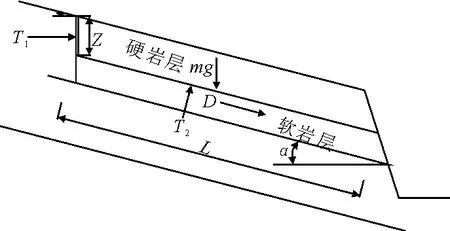
图1 分析力学模型

由图1可见，滑坡硬岩层后缘形成宽大拉裂缝，为雨水的渗入提供了有利条件.强降雨时，地下水在边坡后缘张裂隙和潜在滑动面形成的渗流通道中运动时，对滑体将产生3个方面的力学作用：张裂隙静水压力、潜在滑动面扬压力和动水压力，其表达式分别为

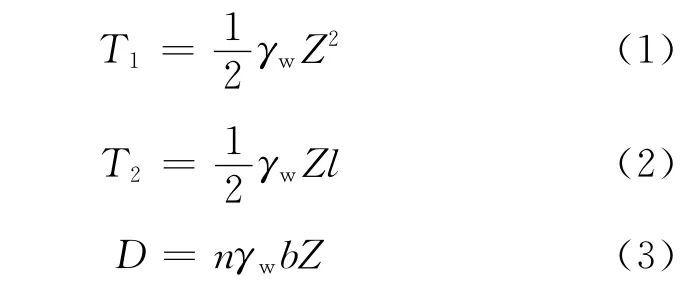
式中：n为滑动面上面壁上岩土体的给水度；b为滑动面的层面开度；Z为后缘张裂隙的充水高度；l为滑动面的长度；γw为水的水容重.

从式（1）～（3）可以看出，强降雨时，张裂隙静水压力、潜在滑动面扬压力和动水压力的大小均取决于边坡后缘的张裂缝充水高度，因此，边坡稳定性分析时后缘张裂隙充水高度是一个极其重要的参数.边坡平面滑动采用刚体滑移模型进行分析，设滑面内摩擦角为φ、粘聚力为c，则坡体在重力作用和水力作用下的抗滑力T和下滑力R分别为

1.2 敏感度计算

敏感度分析是指通过计算一个自变量发生变化时所引起的因变量的改变率，从而分析该自变量对因变量的贡献［5］.

边坡稳定性的敏感度分析主要是研究影响边坡稳定性的各因素与相应的稳定性系数之间的相互关系.它由各因素的相对变化率与边坡稳定性系数的相对变化率之间的比值来进行衡量，即第i个影响因素的敏感度Si可表示如下［6－7］

式中：｜ΔXi／Xi｜为影响因素 Xi的相对变化率；｜ΔKi／Ki｜为稳定性系数Ki的相对变化率.

2 边坡敏感性分析

2.1 层面强度的敏感性分析

计算的物理力学参数如下：c＝100kPa，φ＝20°，a＝16°，岩体容重γ＝26kPa／m3，h＝25m.图2～3分别为a＝16°时边坡稳定性系数随层内内摩擦角和粘聚力变化的关系.可以看出，边坡的稳定性随层面内摩擦角或粘聚力的提高显著提高；不同岩层厚度或粘聚力情况下，内摩擦角与稳定性系数基本上保持线性关系，对边坡稳定的影响规律是一致的，而粘聚力对边坡稳定性的影响与岩层厚度有一定的关系，岩层厚度越小，图3中曲线斜率越大，粘聚力对边坡稳定性影响越显著，此时，粘聚力对边坡稳定性贡献越大.当保持其他参数不变时，改变粘聚力c（变化范围为10～330 kPa），计算求得粘聚力的敏感度为Si＝0.149；改变内摩擦角φ（5°～45°），计算求得内摩擦角的敏感度为Si＝1.007 1，可见内摩擦角的敏感度比粘聚力的大得多.

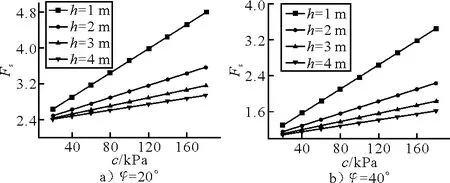
图2 边坡安全系数与层面粘聚力的关系曲线图

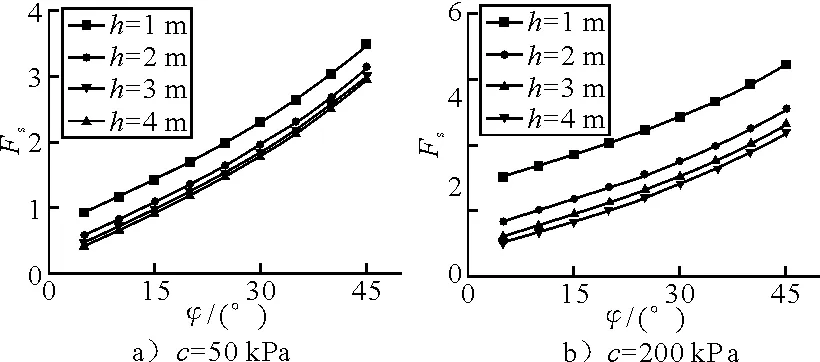
图3 边坡安全系数与层面内摩擦角的关系曲线图

从滑坡的原理上看，层面的粘聚力和内摩擦角越高，则构成沿层面的抗滑动力越大，边坡的稳定性就越好；反之，值越低，边坡的稳定性就越差.所以，软硬交互型岩质边坡是否能滑坡实质上受层面粘聚力和内摩擦角控制.因此，在对软硬交互型岩质边坡的滑坡进行处置技术和优化方法选择时，应重点放在如何直接或间接地提高层面的粘聚力和内摩擦角的措施上，从而达到提高坡体稳定性的目的.

2.2 层面厚度的敏感性分析

岩层厚度是影响边坡稳定性的一个重要因素，设W＝hlγ，则式（5）变为

式中：h为岩层厚度；γ为岩体的容重.

由式（8）可知，岩层厚度越大，边坡稳定性越低，其原因主要有两方面：一方面，在不考虑水力作用时，由式（8）可化简得：

所以，边坡在自身重力下随着岩层厚度增加，其稳定性降低.

另一方面，从式（8）可知，贯通岩层层面的扬压力和后缘张裂缝静水压力沿潜在滑动面上的有效法向应力均减小了边坡的抗滑力；张裂隙静水压力潜在滑动面向上的分力和岩层面上的动水压力增加了边坡的下滑力.而这3种力的大小均取决于边坡后缘张裂隙充水高度，由于岩层厚度与后缘张裂缝充水高度有着直接的关系，所以，岩层厚度越大，水力作用对边坡稳定性不利作用表现得越强烈，稳定性系数降低得越多.图4为层面倾角a＝16°，层面粘聚力c＝100kPa为绘制的边坡的稳定性系数与岩层厚度的关系.

图4 稳定性系数与岩层厚度关系曲线

从图4可以看出，在岩层厚度较薄时，图中曲线的斜率较大，随着岩层厚度的增大，曲线逐步变为近水平状；另外，观察φ＝15°曲线，在岩层厚度较薄时，边坡是稳定的，岩层厚度超过6m后，边坡处于不稳定状态.这说明了滑带的发展与岩层厚度有关，即存在一临界岩层厚度hmax，当岩层厚度大于hmax，软弱结构面才可能发展成为滑带.

改变岩层厚度h（变化范围为5～45m），计算求得岩层厚的度敏感度为Si＝0.278 1.

2.3 层面倾角的敏感性分析

岩层倾角是软硬岩互层边坡稳定性分析的重要指标.图5为层面摩擦角＝20°，岩体重度γ＝26 kPa／m3，不同岩层厚度下边坡稳定性系数与岩层倾角的关系曲线.图5a）表示潜在滑动面维软弱层面粘聚力较小的情形，图5b）表示潜在滑动面为软弱层间错动带或泥化夹层、粘聚力较大情形，边坡的稳定性与岩层倾角的关系.可以看出，在其他参数不变的情况下，边坡稳定性随着岩层倾角的增加而急剧降低，所以边坡稳定性对层面倾角较为敏感.改变岩层倾角（变化范围5°～45°），计算求得岩层倾角的敏感度为Si＝1.022 5.

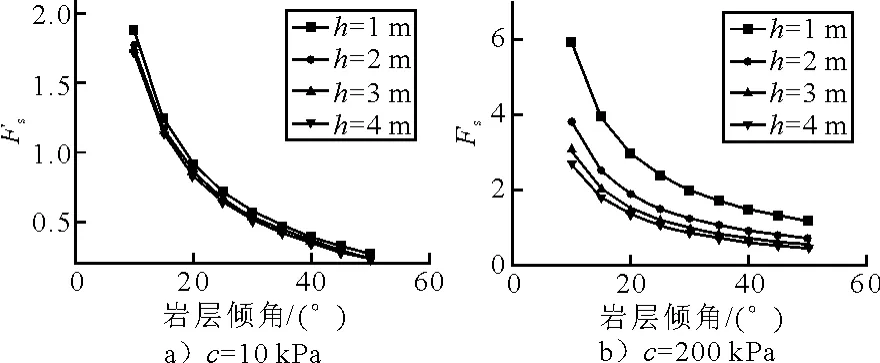
图5 边坡的稳定性与岩层倾角的关系

从图5a）可以看出，当岩层倾角略大于16°（小于层面内摩擦角20°）时，边坡即达到临界稳定状态，按理说，此时的岩层倾角应该和层面内摩擦角基本上相等，究其原因是：边坡中的水力作用能使得边坡的稳定下降，其对边坡稳定性不利作用的贡献约等于层面倾角与层面内摩擦角之差的角度对边坡稳定性的贡献程度.所以，不考虑边坡中的水力作用，当边坡处于临界状态时，此时的岩层倾角应该和层面内摩擦角基本上相等，见表1.而从图5b）可以看出，在层面粘聚力较大时，边坡破坏时的层面倾角远大于层面内摩擦角.

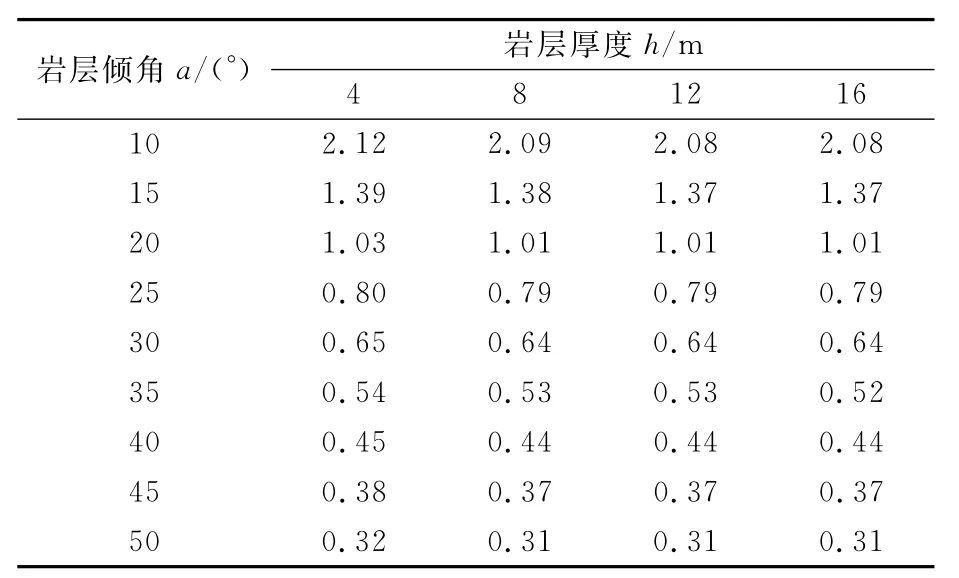
表1 不同岩层倾角的边坡安全系数（c＝200kPa时）

2.4 水力作用的敏感性分析

上述在讨论层面强度、层面厚度和层面倾角对边坡的敏感性因素分析时，均考虑在强降水的情况下，即后缘张裂缝充满水后.而大多数情况下，边坡后缘的张裂缝中不一定都充满水.现在来讨论边坡对水力作用的敏感性，也就是假设后缘张裂缝在不同程度的充水情况下水力作用对边坡稳定性的影响.当不考虑边坡中地下水的水力作用时，边坡的稳定系数Fs为1.36，当考虑张裂缝中水深变化时水力作用对边坡稳定性的影响时，计算结果见图6.

图6 边坡稳定性系数与张裂缝中水深的关系

从图6可知，边坡的稳定系数在水力作用的影响下随张裂缝中水深的变化而急剧下降.当水位深度为5m时，水力作用使稳定系数降低了2.48%；当水位深度为10m时，水力作用使稳定系数降低5.19%；当水位深度为15m时，水力作用使稳定系数降低了8.12%；当水位深度为20 m时，水力作用使稳定系数降低了11.23%；当水位深度为25m时，水力作用使稳定系数降低了14.53%所以，水力作用对边坡稳定性的影响较大，是触发边坡失稳的关键因素.计算求得水力作用的敏感度为Si＝0.149 8.

文献［8］通过物理实验研究表明：随着注水的进行，边坡岩体位移均保持增长.第一层注水时，边坡岩体的位移均较小，边坡均未发现裂缝；而在第二层软岩注水约121h，测点的变形发生明显的突变，坡体变形加速，位移均较大，此时在边坡前缘存在明显的裂隙.在注水约196h后，模型体后缘自软化层起的以上部分开始脱离框架.当改变岩层倾角时，边坡即发生前缘的剪切破坏.说明明层面倾角和软弱层面的强度参数（内摩擦角）对边坡稳定性起主要控制作用，岩层厚度对的稳定性也有明显的影响.所以物理模型试验所得的对软硬岩边坡稳定性影响的规律与本文所得规律的是一致的.