基于遗传算法的多信道无线网络信道分配方案

刘耀中，余旭涛

(东南大学毫米波国家重点实验室，南京 210008)

1 概述

在传统的单信道无线网络中，多个节点同时传输时，彼此间的干扰会带来容量降低的问题。尤其是节点密度增加将加剧节点间的竞争和发送分组之间的冲突，同时，大量的节点退避降低了信道利用率，并导致吞吐量的迅速下降。因此，信道干扰成为影响无线网络容量的重要因素。而在多信道无线网络中，节点可以用不同的信道发送和接收数据，从而减少冲突。由于信道数目受限，因此如何合理有效地利用多信道技术增加无线网络并行传输的链路数目，提升无线网络的吞吐量，成为无线网络研究中的关键问题之一。多信道网络的性能与网络中可用信道的数目以及通信时采用何种信道分配方案相关。一个好的信道分配策略，能够降低无线链路之间的干扰，提高无线网络的吞吐量，优化网络的性能和降低网络通信时数据的丢包率。因此，多信道无线网络中信道分配成为研究的热门话题。

目前，已提出多种信道分配方案，如按需动态信道分配(Dynamic Channel Assignment,DCA)[1]协议，DCA协议中每个节点配置 2个无线接口，其中，一个接口固定工作在控制信道上传输控制信息；另一个接口在其余的信道上进行切换，完成数据传输的任务，通过节点同时侦听控制信道和数据信道，有效降低了冲突。文献[2]研究信道数小于接口数的情况，在固定部分接口卡的情况下，提出一种可以平衡网络负载的信道分配和信道切换策略。文献[3-4]提出一种基于学习的多接口信道分配协议(Learning-based Channel Allocation Protocol,LCAP)，LCAP通过自动从邻节点学习信道的使用信息，从而自适应地进行高效率的信道分配。文献[5]提出一种混合信道分配策略，根据相邻节点使用相同信道的固定接口数目分配信道。信道跳跃多址接入(Channel Hopping Multiple Access,CHMA)协议[6]首先将时间划分为若干个时隙，网络中的节点按照同样的顺序进行工作频率的跳变，在同一个时隙里网络中的所有空闲节点处于同一工作信道。如果节点有数据需要发送，则先发送一个请求发送包，接收节点收到请求发送包后在下一跳回复一个清除发送包，这样收发节点将停留在此信道上完成数据的传输。分割插入信道跳跃(Slotted Seeded Channel Hopping,SSCH)协议[7]同样使用了信道跳跃技术，但是各个节点的信道跳跃顺序并不相同，节点根据伪随机序列同步切换信道，且每个节点都有多个序列，每个序列都由唯一的伪随机序列发生器产生。网络中任意 2个节点至少有一个时隙停留在同一信道，这样网络中的各个节点就可以通过广播来了解各自的信道调度情况。

本文针对单接口多信道无线网络，提出一种基于改进自适应遗传算法的多信道无线网络信道分配方案。建立多信道无线网络信道分配问题的数学模型，将信道分配问题转化为相应的优化问题。采用遗传算法对其进行求解，针对传统遗传算法容易早熟和局部收敛的缺点，对传统遗传算法进行改进，使用新的交叉方式，并且使算法能够在运行的过程中自适应地调整相应的参数。

2 多信道无线网络信道分配模型

对于一个由 n个节点组成的多信道无线网络，设节点存在l条链路，有c个正交的无线信道可以同时传输数据。用顶点v(v∈V)表示网络中的节点，如果2个节点之间存在通信链路，则用一条边e(e∈E)表示，这样就得到网络的拓扑图G(V,E)，然后用顶点v’(v’∈V’)表示网络拓扑图的边，若在单信道情况下，2个顶点所对应的链路间存在冲突，则用一条边e’(e’∈E’)将2个顶点相连，这样便由网络的拓扑图 G(V,E)得到网络冲突图G(V’,E’)，再由网络冲突图G推出网络的冲突矩阵A，网络冲突矩阵A为一个l×l的矩阵，用来描述网络中链路间的冲突情况。根据冲突矩阵A求信道分配矩阵B。

对单信道的无线网络，根据冲突图可以得到网络冲突矩阵A=[aij]l×l，矩阵中各元素取值如下：

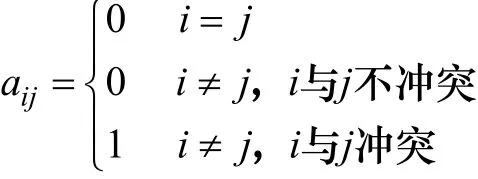
其中，i和j表示网络拓扑图中的链路，1≤i≤l，1≤j≤l，i和j都为自然数。

网络中如何给各个链路分配信道，用道分配矩阵B来表示。假设可用信道数目为 c，在信道分配矩阵 B=[bij]l×c中，每一行有且仅有一个元素为 1，其余元素为 0，即若bij=1，表明第i条链路被分配到第j个信道上。另外，用列向量Bj表示矩阵B的第j列，Bj描述了网络中的链路分配到第j个信道的情况。因为网络的冲突矩阵A中，取值为1的元素总和代表在单信道的情况下，网络所有链路之间总的冲突值，所以表示所有被分配到第j个信道链路之间的冲突值，整个网络的冲突值可用来表示，即所有信道对应冲突值的总和。因此，信道分配问题可以归结为求矩阵 B=[bij]l×c，使得网络冲突值最小：

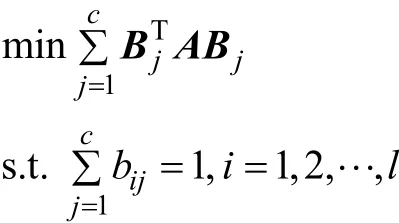
3 改进的自适应遗传算法

本文采用遗传算法解决上述极小化问题，遗传算法是模拟生物的遗传进化过程而形成的全局优化概率搜索算法[8]。对于传统的遗传算法来说，控制参数是在遗传进化中保持不变的，因此，容易出现早熟和局部收敛。而自适应遗传算法可以实现参数的可变，能够使交叉率和变异率随群体的适应度自适应改变，能提供相对某个解的最佳交叉率和变异率[9]。与传统遗传算法相比，自适应遗传算法的交叉率与变异率不是一个固定值，而是按群体的适应度进行自适应调整[10]。

本文使用一种改进的自适应遗传算法[11]，该算法采用了一种新的交叉方式，增强算法的全局搜索能力，同时，能够在优化过程中，根据具体情况自动调节交叉概率和变异概率，避免算法陷入局部最优，从而显著提高搜索效率。

该遗传算法将进化过程分成 2个部分：初期和后期。在初期执行固定参数的遗传操作，在后期执行自适应遗传操作。这样可以在初期让优良的染色体也有较大的机会参与交叉运算，提高种群的多样性。为了防止出现局部最优的情况，本文算法提出一种新的交叉方式。每次遗传操作后，将所有的染色体按照适应值大小排序并分为 2组，即将高适应值的染色体分为一组，剩下的为另一组。在交叉操作之前，分别从 2组中各随机选一个染色体进行交叉运算，这样可以让最优的染色体和最差的染色体有较大的交叉概率，整个染色体种群的适应值同时向最优解靠近，防止了局部最优的出现。该算法在生成子代时，采用父子竞争机制的原理，两父代交叉产生2个新一代，当2个子代中具有最大适应值的个体值大于父代中具有最大适应值的个体时，认为子代优于父代，将子代替换父代，否则，保留父代，让其进入下一轮的进化。这样，就不会只要进行交叉算子操作子代就替换父代，而是在父子两代中选择最优的个体进入下一代，子代总是优于它们的父代，进化总是朝着最优的方向发展。

改进的自适应遗传算法过程如下：

步骤1 进行编码设计，并生成初始群体。

步骤2 定义适应度函数，计算各个个体的适应度fi。

步骤3 计算群体的平均适应度favg和最大适应度fmax，将群体按适应值大小排序并分为2组。

步骤4 进行交叉操作，首先判断种群的代数，若小于n，执行固定的交叉概率；若大于等于 n，执行自适应交叉概率。n为执行固定参数遗传操作的代数，自适应交叉概率Pc如下：

其中，fc为要交叉的2个个体中较大的适应度值；favg为群体的适应度平均值；fmax为群体的最大适应度；k1、k2为预先设定的常数。

步骤5 进行变异操作，首先判断种群的代数，若小于n，则执行固定的变异概率；若大于或等于 n，则执行自适应变异概率Pm如下：

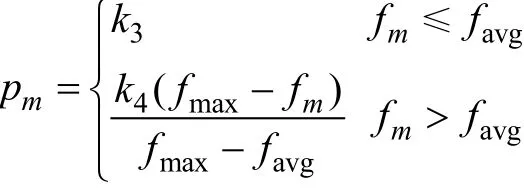
其中，fm为要变异个体的适应度值；k3、k4为预先设定的常数。

步骤6 计算由交叉和变异生成的新个体的适应度，构成新一代群体。

步骤7 判断是否达到预定的迭代次数。如果是，则结束寻优过程；否则，转步骤4。

4 编码方式及参数设置

遗传算法有二进制编码方式、实数编码方式和整数编码方式[12]。本文采用整数编码的方式。对于一个可行解矩阵B(l×c)，可以用一个l维的向量M表示，向量中每个元素的取值范围为1,2,…,c。比如一个l为8，c为4的矩阵B表示为：

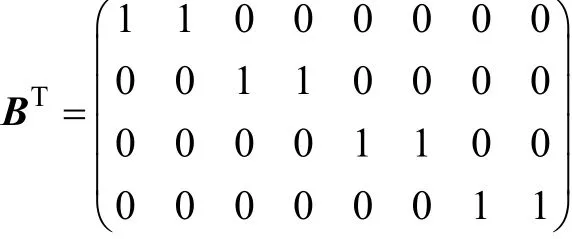
对应的l维向量M为(1,1,2,2,3,3,4,4)。

向量M第i个元素的值x代表矩阵BT第i列的第x行元素为1，而其余行的元素为0。比如M中第8个元素值为4，在BT中对应第8列第4行的元素为1。

随机生成200个个体作为初始群体，即200个l维向量，向量中每个元素的取值范围为1,2,…,c。然后，采用轮盘赌选择方式从种群中选择个体。即每个个体进入下一代的概率等于它的适应度值与整个种群中个体适应度值总和的比例。一个个体被选择的概率由下式给出：

其中，f(xi)是个体 xi的适应度；F(xi)是这个个体被选择的概率。

采用单点交叉的方式产生新的种群。对于2个长度为k的向量P、Q，选择一个均匀分布的随机整数m，在[1,k−1]间，在P和Q间交换m+1～k之间的各变量。另外，步骤4中的k1、k2分别设定为0.8和0.9。同时，步骤5中的k3、k4均设定为 0.05，n设定为50，即执行固定交叉率和变异率的遗传代数为50。同时，设定最大遗传代数为300。

5 仿真结果与分析

图1是一个包含10个节点的无线网络拓扑。

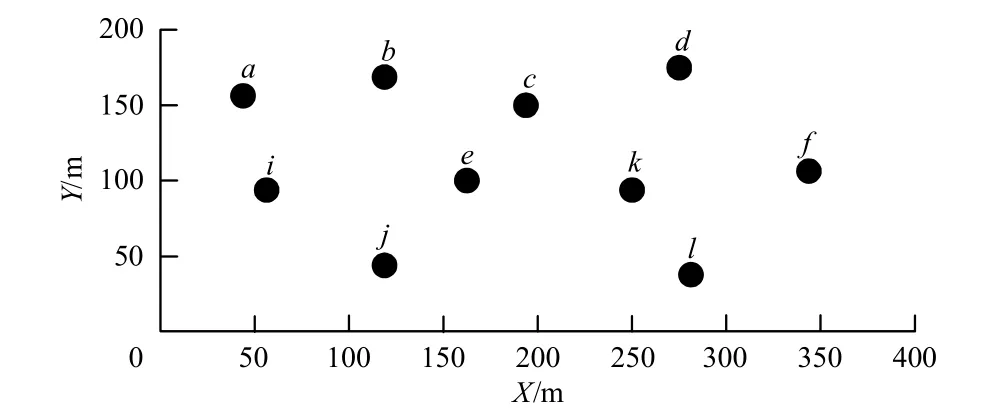
图1 含有10个节点的网络拓扑

10个节点分布在400 m×200 m的区域中。如果2个节点a和节点b之间的距离小于节点的发送距离，则节点a和节点b之间存在一对双向链路，即以节点a为发送节点，节点b为接收节点的一条链路和以节点b为发送节点，节点a为接收节点的一条链路。当节点发送距离为150 m时，一共存在 52条链路，于是可以得出一个 52×52的冲突矩阵。其中，冲突矩阵中1的数目为2268。所以，当信道数为c时，如果采用随机的方式把52条链路分配给c个信道，则网络中链路的冲突值为2268/c。而根据遗传算法可以求出当信道数为 c时，目标函数值的变化，取出其中的最小值，即为使用遗传算法分配信道时对应的冲突值。

图2是信道数c=4时，采用简单遗传算法和改进的自适应遗传算法进行信道分配对应的网络冲突值对比，通过简单遗传算法得到的分配矩阵B对应的网络冲突值为444，而通过改进的自适应遗传算法得到的分配矩阵B对应的网络冲突值为432。通过图2的比较可以看出，使用改进的自适应遗传算法比使用简单遗传算法的收敛速度更快，当遗传代数为 100时，采用简单遗传算法求解得到的网络冲突值仅收敛到454，而遗传代数同样为100时，采用改进的自适应遗传算法求解得到的网络冲突值已收敛到442。且采用改进的自适应遗传算法求解所得到的解对应的网络冲突值更小，因此，所求的解更加逼近最优解。另外，整个种群个体对应的网络冲突值的均值更小，正如前面提到的，整个种群的适应值同时向最优解靠近。

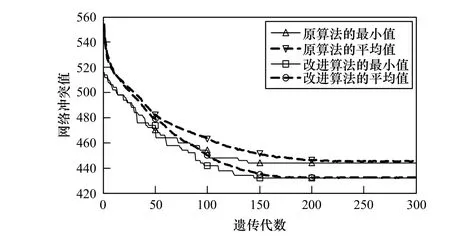
图2 算法改进前后的网络冲突值对比

图3显示了信道数分别为3、5和7时，网络冲突值随遗传代数的变化。

图3 不同信道数对应的网络冲突值

采用改进的自适应遗传算法所求的网络冲突值分别为624、332、208。在每条实线的上方的虚线分别对应不同的信道数的情况下，采用随机方式分配信道相对应的网络冲突值，在信道数为3、5和7的情况下，分别为756、454、324。从图3可以看出，采用改进的自适应遗传算法进行链路分配可以大幅降低网络的冲突，尤其在信道数较多的情况下效果更为明显。

当节点发送距离为100 m时，以上的网络拓扑图中一共存在28条链路，于是可以得出一个28×28的冲突矩阵。其中，矩阵中1的数目为500。同样，当信道数为c时，如果采用随机的方式把28条链路分配给c个信道时，则链路的冲突值为 500/c。而采用改进的自适应遗传算法求解，信道数分别为3、5和7时，网络冲突值随遗传代数的变化如图4所示。

可以得到最终解对应的网络冲突值分别为108、48、22。从图4可以看出，相比于发送距离为150 m的情况，其网络冲突值的下降幅度更为明显。

图5和图6采用条形图比较了信道数不同，发送距离为100 m(网络中一共存在28条链路)、150 m(网络中一共存在52条链路)时，采用随机分配方式和使用改进的自适应遗传算法分配链路对应的网络冲突值。可以看到，采用改进的自适应遗传算法进行网络链路分配相比于随机的链路分配方式，可以显著地减小网络的冲突值，尤其在网络中的可用信道数较多，以及网络节点发送距离较小、冲突矩阵稀疏时，效果更为明显。如发送距离为100 m，信道数为7时，采用改进的自适应遗传算法进行网络链路分配得到的网络冲突值仅为随机的分配方式对应网络冲突值的30%。

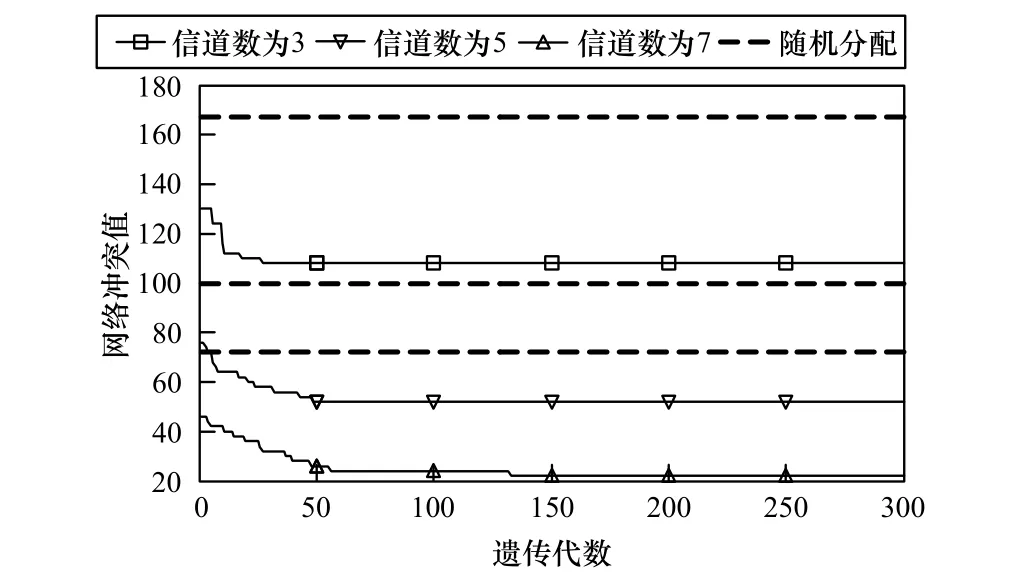
图4 发送距离为100 m时不同信道数对应的网络冲突值

图5 发送距离为100 m时2种分配方式的网络冲突值

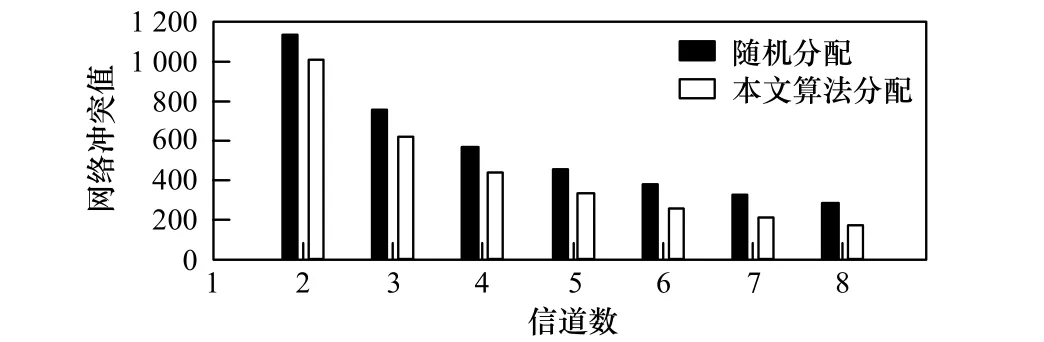
图6 发送距离为150 m时2种分配方式的网络冲突值

6 结束语

针对单接口多信道无线网络的信道分配问题，本文提出一种改进的自适应遗传算法。利用冲突图的概念为网络建立模型，进而导出网络的冲突矩阵，将问题转化为求信道分配矩阵，使网络冲突值最小，通过对信道分配矩阵进行合适的编码，从而利用遗传算法加以解决。仿真结果表明，该算法进行分配可以大幅降低网络的冲突值，从而提升网络的性能。本文仅考虑了单接口多信道的情况，给每个节点配备多个接口可以进一步降低网络的干扰，因此，今后将对多接口多信道网络进行研究。

[1]Wu Shih-Lin,Lin Chih-Yu,Tseng Yu-Chee,et al.A New Multi-channel MAC Protocol with On-demand Channel Assignment for Multi-hop Mobile Ad Hoc Networks[C]//Proc.of International Symposium on Parallel Architectures,Algorithms,and Networks.Dallas,USA: IEEE Computer Society,2000.

[2]He Pingshi,Xu Ziping.Channel Assignment and Routing in Multi-channel,Multi-interface Wireless Mesh Networks[C]//Proc.of the 2nd Computer Engineering and Technology.Chengdu,China: IEEE Press,2010.

[3]Ghosh A,Hamouda W.Cross-layer Antenna Selection and Channel Allocation for MIMO Cognitive Radios[J].IEEE Transactions on Wireless Communications,2011,10(11):3666-3474.

[4]Pediaditaki S,Arrieta P,Marina M K.A Learning-based Approach for Distributed Multi-radio Channel Allocation in Wireless Mesh Networks[C]//Proc.of the 17th IEEE International Conference on Network Protocols.Princeton,USA: IEEE Press,2009.

[5]Kyasanur P,Vaidya N.Routing and Link-layer Protocols for Multi-channel Multi-interface Ad Hoc Wireless Networks[J].Mobile Computing and Communications Review,2006,10(1):31-43.

[6]Tzamaloukas A,Garcia J J,Channel-hopping Multiple Access[C]//Proc.of International Conference on Communications.New Orleans,USA: IEEE Press,2000.

[7]Paramvir B,Chandra R,Dunagan J.SSCH: Slotted Seeded Channel Hopping for Capacity Improvement in IEEE 802.11 Ad-hoc Wireless Networks[C]//Proc.of the 10th Annual International Conference on Mobile Computing and Networking.New York,USA: ACM Press,2004.

[8]Holland J H.Adaptation in Natural and Artificial System[M].[S.l.]: MIT Press,1975.

[9]Srinivas M,Patnaik L M.Adaptive Probabilities of Crossover and Mutation in Genetic Algorithm[J].IEEE Transactions on System,Man and Cybernetics,1994,24(4): 656-667.

[10]梁 旭,黄 明.现代智能优化混合算法及其应用[M].北京: 电子工业出版社,2011.

[11]梁 霞,梁 旭,黄 明.改进的自适应遗传算法及其在作业车间调度中的应用[J].大连铁道学院学报,2005,26(4):33-35.

[12]雷英杰,张善文,李续武,等.遗传算法工具箱及应用[M].西安: 西安电子科技大学出版社,2005.