自然地形下六足步行机器人基于落足点的位姿调整策略
2013-08-16赵龙海刘玉斌尹旭悦许文韬
赵龙海, 刘玉斌, 赵 杰*, 尹旭悦, 许文韬, 张 赫
(1.哈尔滨工业大学机器人技术与系统国家重点实验室,黑龙江哈尔滨150080;2.长春科技学院汽车机械工程学院,吉林长春130600)
多足步行机器人是一种具有冗余驱动、多支 链、时变拓扑运动机构的特种机器人,其运动规划与控制具有挑战性,其中许多基础理论和技术问题亟待解决,是机器人领域的一个重要研究方向,也是国内外研究人员广泛关注的热点之一[1]。多足机器人的应用范围非常广泛,据调查,地球上近一半的地面不能为传统的轮式或履带式车辆所到达,但很多足式动物却可以在这些地面上行走自如。因此,仿生多足机器人的运动方式具有其他地面推进方式所不具有的独特优越性[2],研究多足机器人在自然地形中全方位运动的规划策略具有重要意义。
六足步行机器人运动效率与稳定性是一对相互制约的因素,提高效率往往会带来稳定性方面的问题。近年来,国内外专家学者及机构在六足步行机器人系统的运动规划方面取得了很多进展,然而目前仍未获得能够兼顾机器人步行效率和稳定性的运动规划算法。Belter D等[3]讨论了六足步行机器人在自然地形下的运动规划,但没有考虑位姿调整以及运动效率问题;该课题组[4-5]同时研究自然地形中落足点选取问题,在文献[6]中提出了躯干位姿的优化策略,但仅适用于准静态运动,并且不能提高机器人在整个运动过程的稳定性以及运动效率;Lin P C等[7]讨论了躯干位姿的评估方法,但没有提出根据地形自适应调整躯干位姿的方法;Doroftei I等[8]系统地给出六足步行机器人研究思路,但对具体实现方法没有论述。
文中致力于弥补上述各方法的不足,提出了一种基于落足点的机器人位姿调整策略,并通过仿真实验验证了该策略的有效性。
1 基于地面参考系的六足步行机器人运动学
1.1 HITCR-Ⅱ六足步行机器人的参数
六足步行机器人HITCR-Ⅱ如图1所示,每条腿各有3个关节,可以通过标准D-H矩阵对其进行运动学分析。

图1 六足步行机器人HITCR-ⅡFig.1 Hexapod walking robot HITCR-Ⅱ
图2 为六足步行机器人运动学模型,躯干坐标系建立在机器人的质心。
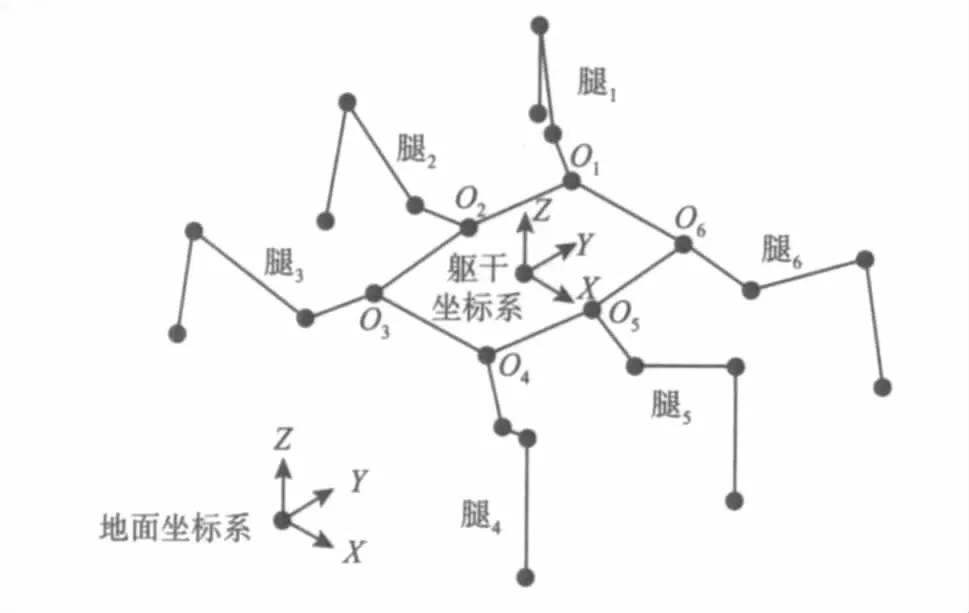
图2 六足步行机器人HITCR-Ⅱ的数学模型Fig.2 Mathematical model of the hexapod walking robot HITCR-Ⅱ
表1 为HITCR-Ⅱ的位姿参数。其中:GT列为躯干坐标系相对于地面坐标系的位姿关系,TO1至TO6列为6条腿的基坐标系相对于躯干的位姿关系,表2为腿部各连杆的参数,表3为腿部标准D-H参数表。
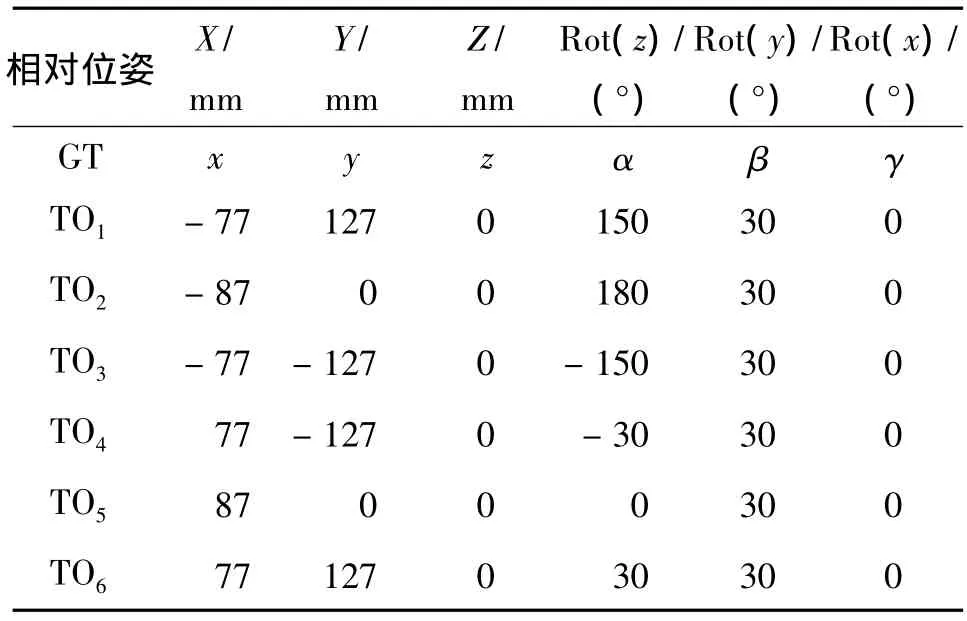
表1 HITCR-Ⅱ的位姿参数Tab.1 Pose parameters of the hexapod walking robot HITCR-Ⅱ

表2 HITCR-Ⅱ的腿长参数Tab.2 Leg parameters of HITCR-Ⅱ

表3 HITCR-Ⅱ的腿部D-H参数Tab.3 Leg's D-H parameters of HITCR-Ⅱ
1.2 运动学分析
根据表1中GT列的参数可以建立躯干坐标系相对于地面坐标系的转换矩阵,具体如下:

每条腿的基坐标系相对于躯干坐标系固定,将表1中TO1至TO6列的参数分别代入式(1)中可得到它们之间的转换关系。
根据图3中建立的坐标系和表2、表3中的参数,通过D-H法建立起机器人运动学数学模型,并得到各足足端相对于其基坐标系的位置关系,即

根据式(1)可以求得各足足端相对于躯干坐标系和地面坐标系的位置。通过式(2)可以求取各个关节角 θ1,θ2和 θ3。
2 基于落足点的六足步行机器人自然地形位姿调整策略
六足步行机器人在移动过程中,其位姿调整极其重要。文中提出一种基于落足点的位姿调整策略,可以用于多足机器人的自然地形全方位运动规划,并且适用于各种步态。六足机器人的所有步态中,效率最高稳定裕度最差的是三足步态,因此文中以三足步态为研究基础。
2.1 位置调整策略
各支撑腿的落足点在水平面投影构成一个凸多边形。当机器人的质心水平投影在多边形内时机器人稳定,质心到多边形的最短距离定义为稳定裕度[9]。当机器人的质心水平投影在该多边形的最大内圆圆心处时,机器人具有最大的稳定性,定义该内圆的半径为最大稳定裕度。
2.1.1 运动过程分析 以三足步态行走的六足步行机器人在运动过程中存在两种状态:三足支撑和六足支撑。通常,六足支撑过程机器人的稳定裕度大于三足支撑过程,因为其落足点在水平面投影构成的多边形包含了三足支撑时的情况。但是在机器人以占空比为0.5的三足步态快速行走时,转换过程是瞬时的,则机器人的零力矩点ZMP[10]必须同时落在前后两个支撑相的足端水平投影多边形内部才能保证转换过程中机器人的稳定性,这就使得转换过程成为运动过程中稳定裕度最小的时刻。只有尽可能地提高稳定裕度在最小时刻的最大值才能提高机器人整个运动过程的稳定性。在准静态运动过程中,机器人的零力矩点ZMP即为其质心在水平面的投影。
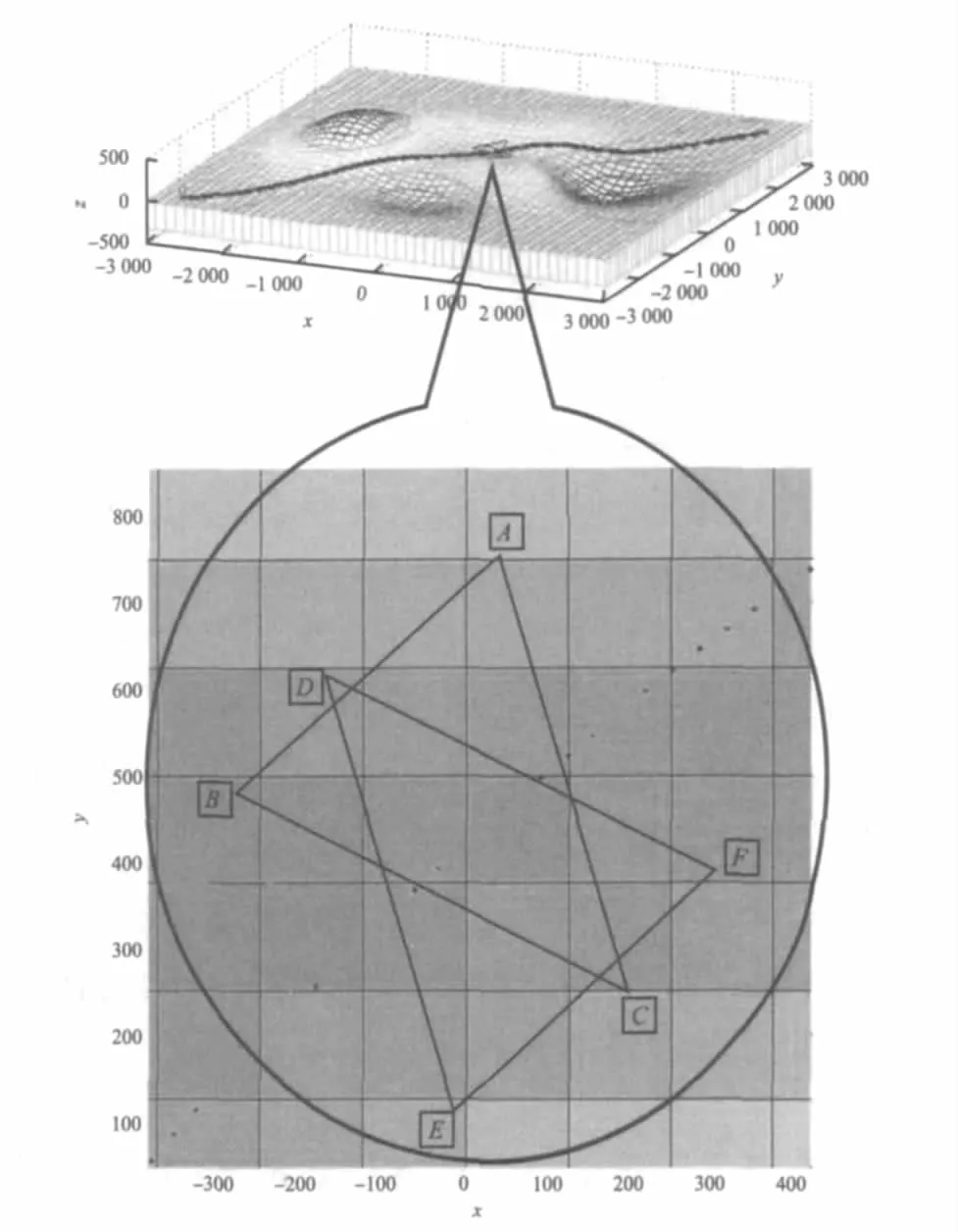
图3 重叠区域的求取方法Fig.3 Method of solving the overlapping area
2.1.2 两个落足多边形水平投影的重叠区域求取方法 三足步态下行走时的情况如图3所示。两个三角形干涉量拓扑图形的类型可归为10种情形[11],考虑到六足机器人的结构限制,位于躯干中间的两条腿不可能超越前腿也不可能落后于后腿,则拓扑情形减少到4种,可以针对每一种情形具体分析。
在自由步态下行走时,落足多边形为不规则多边形。由于多边形都可以被视为若干个顶点为多边形顶点的三角形的组合,利用以下方法可以方便地计算不规则多边形之间的干涉量。设两个落足多边形的水平投影分别有m和n个顶点,则其干涉量的计算可以转化为(m-2)(n-2)对三角形之间的干涉量问题,其干涉量的总和即为这两个多边形之间的干涉量,可以利用多项式求解。
2.1.3 重叠区域的最大内圆圆心及半径的求取方法 通过2.1.2中的方法求得的重叠区域通常为不规则多边形。求N边形最大内圆圆心的原理如下:设有N多边形,①任意两个相邻内角的角平分线相交于Q,求出Q到相邻内角公共边的距离|Q|,则最多存在N距离。②取这些距离最短的一个L,所有多边形的边向内收缩一个距离L,得到一个新的多边形,这个多边形的边数最多为N-1。③如果这个多边形不为三角形和一条线段,则返回①,如果为三角形,求出此三角形的内切圆,则此圆的圆心即为N多边形的最大内圆圆心,此圆半径累加上历次收缩的距离L则为凸多边形最大内圆的半径。当多边形存在平行边,有可能收缩到一条线段。如果收缩到一条线段,则线段上任意一点为最大内圆圆心,历次收缩距离L的累加和为最大内圆半径。
2.1.4 机器人ZMP的调整 通过运动学、动力学分析,设计机器人的运动,保证转换过程中机器人ZMP在该圆心处。半径R即为机器人ZMP到达圆心时的稳定裕度。
2.1.5 重心高度的调整策略 重心高度影响机器人运动的稳定性及灵活性,重心越高,稳定性越差;但重心过低,机器人运动的灵活性差,运动能力下降。重心高度的调整策略应根据具体地形以及机器人的运动需求而定。
2.2 姿态调整策略
机器人的姿态调整主要为了提高机器人的运动能力和稳定性。文中提出了基于落足点信息的多足步行机器人自然地形自适应姿态调整策略。具体内容如下:
1)确定摆动相的足端三角形所在平面;
2)确定支撑相的足端三角形所在平面;
3)插补法计算机器人躯干的姿态。
根据平面方程,用等效轴表示法[12]计算平面的方位角。这两个平面的方位角部分地反应了局部地形信息,可以作为机器人躯干调整的地形参照。
设计合理的权值参数是姿态调整的关键,通过设计不同的权值参数,可以插补得到不同的躯干运动,最基本要求为保证机器人运动过程中位移、速度和加速度连续平缓。首先定义Interpolation为插补点数目,t为插补时刻,v为权值参数。为了得到躯干的平缓运动,可令v随插补时刻变化的关系为

躯干姿态随插补时刻的变化关系如下:

2.3 足端轨迹规划
基于机器人运动学,根据笛卡尔空间中机器人运动的轨迹规划生成关节空间中机器人运动的轨迹,同时生成摆动相和支撑相的足端轨迹。
1)支撑相的轨迹规划:支撑相的足端相对地面静止,躯干相对地面的运动由位姿调整策略确定,因此可求解足端相对于躯干的运动,然后通过逆运动学求得支撑相关节空间的轨迹。
2)摆动相的轨迹规划:根据初始时刻足端相对躯干的位置和躯干到达目标位置后足端相对躯干的位置要求,以及笛卡尔空间中障碍物的参数,合理设计足端相对躯干的运动,继而通过逆运动学求得摆动相关节空间的轨迹。
为了保证机器人运动过程中位移、速度和加速度连续,对足端轨迹规划提出以下具体要求:
1)摆动相转换为支撑相时对地速度为零;
2)支撑相转换为摆动相时对地速度为零;
3)摆动相转换为支撑相时对地加速度为零;
4)支撑相转换为摆动相时对地加速度为零;
5)摆动相摆动过程中足端位置始终高于障碍。
图4 为关节轨迹的规划结果。

图4 关节轨迹Fig.4 Trajectories of the joints
由图4可以看出:在整个运动过程中,关节轨迹是连续的;不同的关节运动轨迹各不相同;机器人行走的步数与关节轨迹中的极值数目相同;地形变化时,关节轨迹会自适应地伴随着变化,使得躯干的姿态适应地形,从而保证机器人运动的效率和稳定性;各个关节的轨迹均在关节的运动能力范围之内。
3 仿真结果分析
为验证文中提出的运动规划策略的正确性,根据机器人的运动能力,在Pro/E中建立了机器人模型和随机地形模型。将模型导入Adams环境,并将根据地形规划得到的关节轨迹作为机器人的输入进行动力学仿真分析。
3.1 验证位置调整策略
图5 为位置调整策略的验证情况。其中,图5(a)为Adams仿真结果,图5(b)为规划结果。比较仿真数据和规划数据,发现两者误差很小,说明仿真结果符合预期规划。这说明位置调整策略在机器人整个运动过程中都起了很好的作用,最终的累积误差也足够小。

图5 位置调整策略验证Fig.5 Diagram of the position adjustment strategy
3.2 验证姿态调整策略
图6 为姿态调整策略的验证情况。其中:图6(a)为Adams仿真结果;图6(b)为规划结果。通过图6中仿真姿态与规划姿态数据比较,发现两者基本一致,证明了位姿调整策略的合理性。
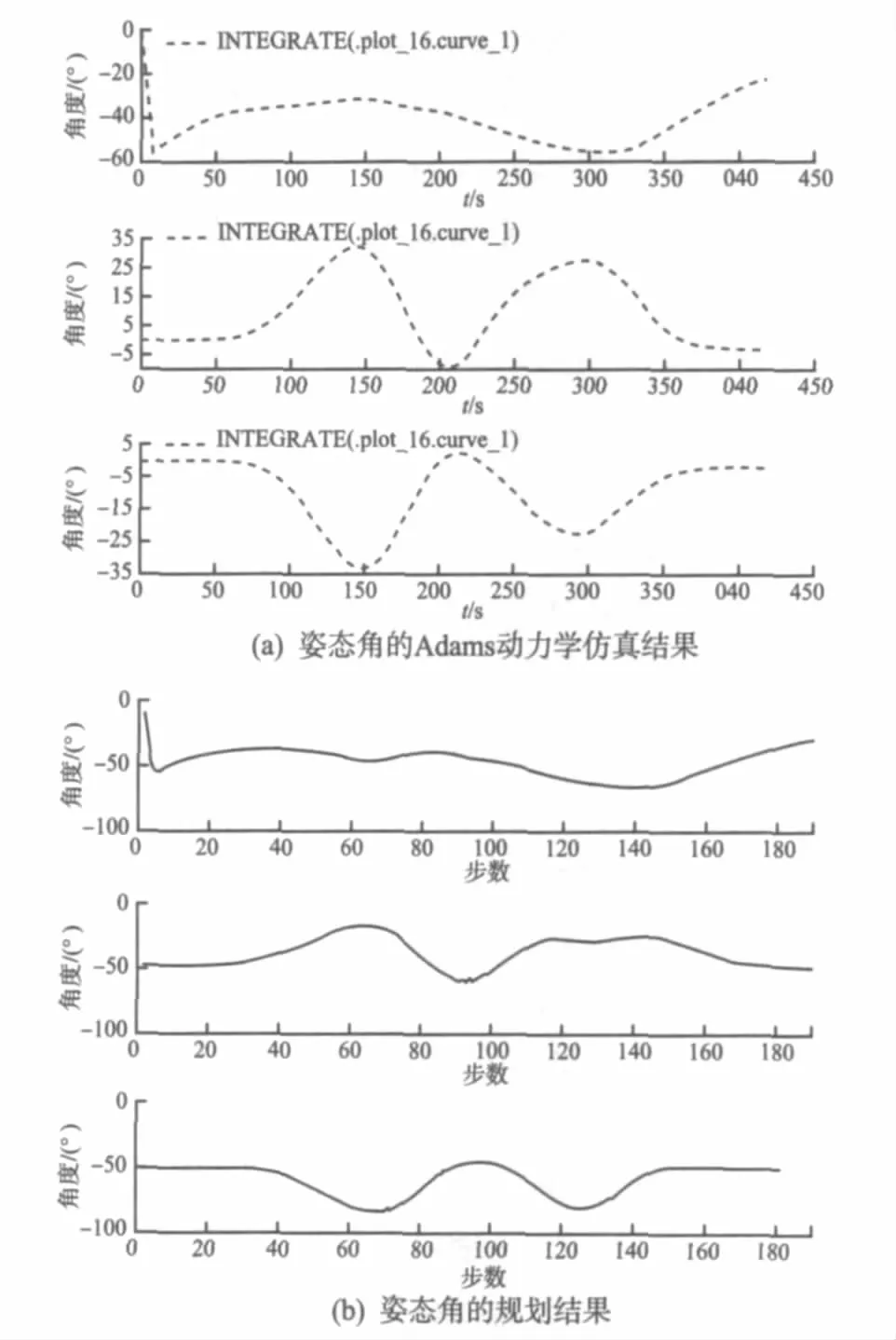
图6 姿态调整策略的验证Fig.6 Diagram of the attitude adjustment strategy
3.3 验证整个运动过程中的稳定性
图7 为整个运动过程中的稳定裕度曲线。通过图7中稳定裕度曲线说明整个运动过程中的稳定性符合预期规划要求。
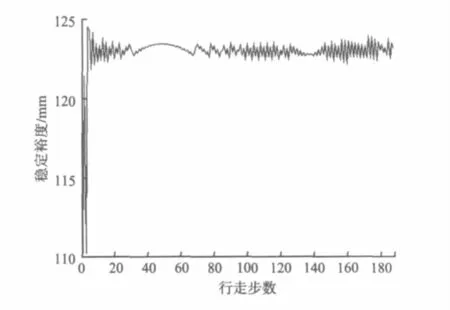
图7 稳定性验证Fig.7 Diagram of the dynamic stability
由图7可以看出,机器人在调整方向时的稳定裕度在110 mm以上,在行走过程中稳定裕度保持在120~125 mm之间,整个运动过程的稳定裕度均在预期范围内。以上数据验证了文中提出的六足步行机器人自然地形全方位运动规划策略的正确性和可靠性。
4 结语
文中提出了一种自然地形下六足步行机器人全方位运动的位姿调整。针对机器人高效率运动时稳定性差的问题,提出了基于落足点的位姿调整策略,并以三足步态为例,通过随机自然地形仿真实验,验证了位置调整策略的效果,说明位姿调整策略使机器人在高效运动的同时具有良好的稳定性,从而能够适应复杂的自然地形,对于多足机器人的应用推广具有深远的意义。
[1]陈学东,孙翊,贾文川.多足步行机器人运动规划与控制[M].武汉:华中理工大学出版社,2006.
[2]罗庆生,韩宝玲.现代仿生机器人设计[M].北京:电子工业出版社,2008.
[3]Belter D,Skrzypczynski P.Integrated motion planning for a hexapod robot walking on rough terrain[C]//18th IFAC World Congress.Milano,Italy:Elsevier,2011:6918-6923.
[4]Belter D,Skrzypczyński P.Rough terrain mapping and classification for foothold selection in a walking robot[J].Journal of Field Robotics,2011,28(4):497-528.
[5]Belter D,Labecki P,Skrzypczynski P.Map-based adaptive foothold planning for unstructured terrain walking[C]//Proceeding of IEEE International Conference on Robotics and Automation ICRA 2010.Anchorage,Alaska:IEEE,5256-5261.
[6]Belter D,Skrzypczynski P.Posture optimization strategy for a statically stable robot traversing rough terrain[C]//Intelligent Robots and Systems(IROS),2012 IEEE/RSJ International Conference on.Alaska:IEEE,2012:2204-2209.
[7]LIN P C,Komsuoglu H,Koditschek D E.A leg configuration measurement system for full-body pose estimates in a hexapod robot[J].Robotics,IEEE Transactions on,2005,21(3):411-422.
[8]Doroftei I,Baudoin Y.A concept of walking robot for humanitarian demining[J].Industrial Robot:an International Journal,2012,39(5):441-449.
[9]McGhee R B,Frank A A.On the stability properties of quadruped creeping gaits[J].Mathematical Biosciences,1968,3:331-351.
[10]Vukobratovic M,Borovac B.Zero-moment point-thirty five years of its life[J].International Journal of Humanoid Robotics,2004,1(01):157-173.
[11]刘德全,滕弘飞.不规则多边形的干涉算法[J].大连理工大学学报,1999,39(5):597-600.LIU Q D,TENG H F.Finite triangular element method of computing overlapping area between two irregularshaped polygons[J].Journal of Dalian University of Technology,1999,39(5):597-600.(in Chinese)
[12]Murray R M,LI Z,Sastry S S.A Mathematical Introduction to Robotic Manipulation[M].Boca Raton Florid,USA:CRC PressI Llc,1994.
