外包生产中的双边道德风险与线性契约设计
2013-08-16张宇婷宋华明
张宇婷,宋华明,杨 慧,许 前
(南京理工大学经济管理学院,江苏南京 210094)
随着社会分工的深入,外包成为企业的重要战略选择。为了降低风险,充分发挥供应商的技术和资源优势,制造商将资源外包的范围扩展到产品零部件的设计研发。此时双方是委托代理关系,制造商是委托人,供应商是代理人。由于利益的冲突,合作关系下隐含着道德风险。从委托人角度出发,防范道德风险是外包契约设计的主要任务之一[1-4]。当双方努力需要花费一定成本且努力水平不可观测时,存在信息不对称。根据信息经济学观点[5],双方都有可能发生道德风险,即双边道德风险问题。
双边道德风险的概念首先由Reid[6]应用于农地承租契约,随后由Rubin[7]将此观念扩展应用于加盟经销商之中。Eswaran[8]将他们的分析限定到线性契约中来研究在双边道德风险情形下的农业生产最优契约。Cooper[9]则正式定义了完全信息与双边道德风险,完全信息是指双方都愿意合作的情况下,追求双方最大的效用总和或最大总剩余;双边道德风险是指双方只追求自身最大利益。Corbett[10]研究了制造商与供应商共同降低间接材料成本时的最优共享收益线性契约。国内对双边道德风险问题研究较少。邓艳红等[11]在双边道德风险模型下,从讨价还价的角度研究了风险投资家和创业者之间的帕累托幼小契约区间确定问题。李丽君等[12]运用委托代理理论探讨了双边道德风险条件下供应链的质量控制策略。
以往的很多文献都假设双方是风险中性的,存在双边道德风险,或委托人是风险中性,代理人是有风险规避性,但只存在单边风险。本文将从委托人是风险中性,代理人有风险规避性,且存在双边道德风险的方面进行探讨。通过比较信息对称和信息不对称环境下线性契约的设计,分析了不确定性、风险厌恶程度、努力的成本系数等因素对线性契约设计的影响。
1 问题描述与模型构建
1.1 问题描述
在现实生产中,制造商将产品部件外包给供应商来生产,以降低生产成本。双方都为最终产品付出了努力,努力水平会影响产品质量,从而影响产品的市场需求。制造商只能观测到最终的市场需求量,而不能观测到供应商所做的努力,双方之间存在信息不对称的情况。根据经济学观点,信息不对称将导致逆向选择及道德风险问题。本文假设制造商是风险中性,供应商是风险规避的,通过比较信息对称和不对称下线性契约的设计,分析风险厌恶程度、能力系数、成本系数等因素对制造商收益的影响,制造商可据此设计合适的激励契约。
1.2 参数定义及基本假设
考虑由一个制造商m和供应商s组成的Stackelberg博弈模型,制造商和供应商的生产成本分别为 c1,c2,努力水平分别为 em,es,产品的最终市场价格为p,市场的销售量Q受到市场条件、制造商的努力程度、供应商的努力程度和市场随机因素的影响,可以表示为:
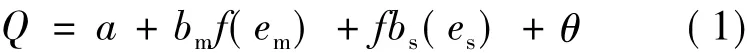
式中:bm表示制造商的能力水平;f(em)表示努力em的产出函数,若f'(em)>0表示制造商努力水平的边际销量为正,即越努力,销量越大,而若f″(em)≤0表示努力的边际销量递减,即努力所导致的销售量的增加速度是递减的;bs表示供应商的能力水平;f(es)表示努力es的产出函数,若f'(es)>0表示供应商的努力水平的边际销售量为正,而f″(es)≤0表示努力的边际销售量递减;a为常数,表示当地市场状况,用固定产出表示。假设a足够大,近似市场销量不会为负。随机变量服从正态分布θ~N(0,σ2)。假设制造商付出努力的成本为c(em),且满足c'(em) > 0,c″(es)≥0;供应商付出努力的成本为 c(es),且满足 c'(es) > 0,c″(es)≥0,即满足成本边际递增。为了简化分析,令f(em)=em,f(es)=es,即销量为努力程度的线性函数。制造商和供应商的努力成本函数分别为
1.3 基本模型构建
制造商为供应商的努力提供一个报酬契约T(Q),该激励合同是基于制造商可观测的变量,即对产品进行研发生产所实现的市场需求Q的线性支付契约:
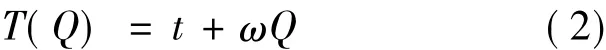
式中:T(Q)为供应商总收入;t为固定收入;ω为产出的分享份额。由于双方边际利润为非负的,ω∈[c2,p-c1]。本文假设制造商是风险中性,其报酬函数就是对其利润函数求期望:
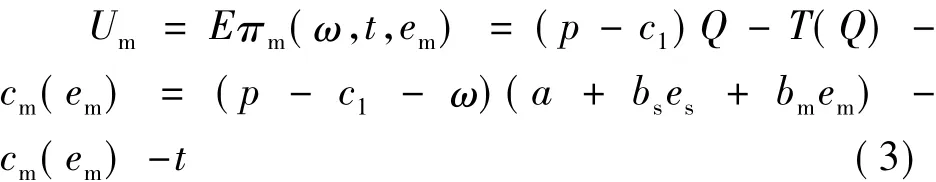
供应商是风险厌恶型,假设其效用函数为负指数效用函数gs(x)=-e-λx,其中λ为风险规避系数,λ>0表示风险规避;λ=0表示风险中性;λ<0表示风险爱好。供应商的报酬函数即期望效用函数为:
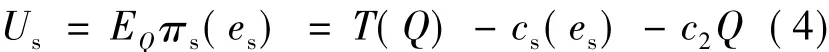
对利润函数πs分别求期望和方差得:
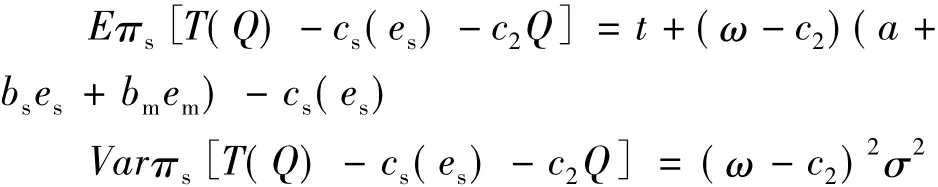
根据确定性等值CE公式推导得:

制造商作为Stackelberg博弈的领导者,在整个博弈中具有“先走一步”的优势,但在追求其自身期望利润最大化时,会受到供应商的激励相容约束(式(6))和个人理性约束(式(7)),其中πs为供应商的保留报酬,这样制造商和供应商的关系可以表述为如下的二层规划模型:
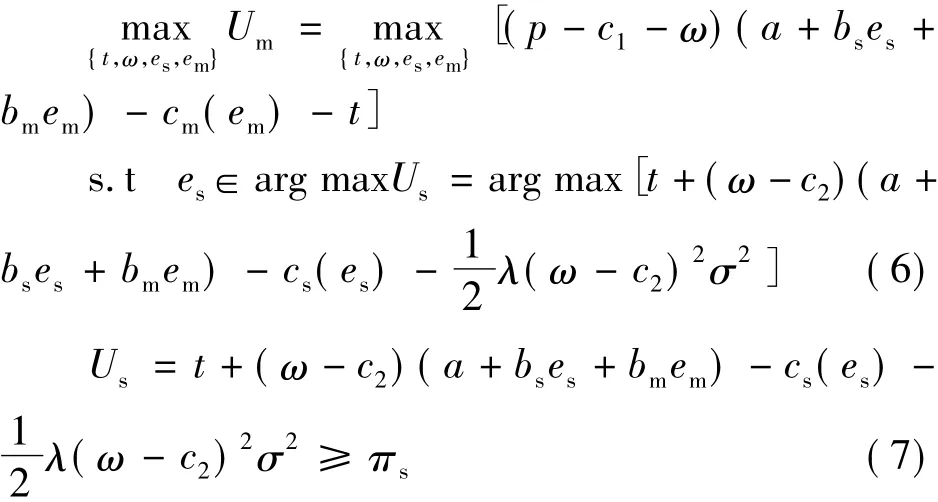
2 信息对称情况下的模型分析
2.1 规划问题求解
在信息对称的情况下,制造商可以观测到零售商的努力水平,所以激励相容约束(式(6))不起作用,令参与约束(式(7))束紧,即Us=πs时制造商报酬最大。因此,规划问题可以改写为:
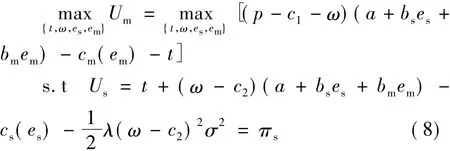
求解可以得到:
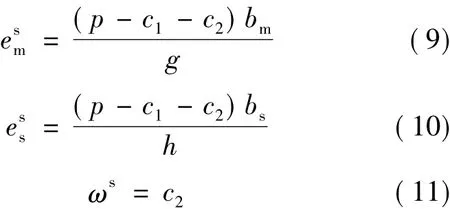
将上述结果带入参与约束的式(8),得到:
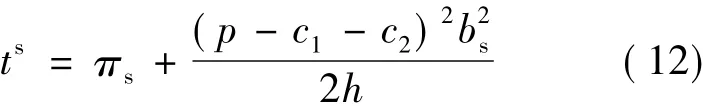
制造商的期望收益为:
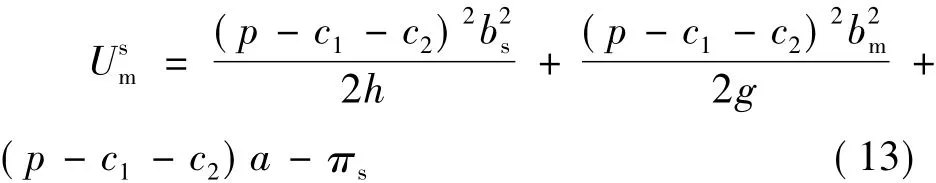
2.2 系统帕累托最优
可见在信息对称情况下,制造商给予供应商的收益分享系数仅满足供应商单位成本要求,固定转移支付仅弥补供应商保留利润和努力成本时,对于制造商是最优解。那么此时最优努力水平对整体供应链,是否达到帕累托最优呢?根据Gan等[13]提出的对于存在风险规避者参与的供应链协调定义,当供应链总体利润最大化并且风险规避约束得到满足时,供应链得到协调,又称为帕累托最优(Pareto Optimality)
最优化问题可以表示为整个研发生产系统的利润扣除双方保留报酬之后的最大化,因为制造商为风险中性,其保留报酬为0:

分别对目标函数(14)中的es和em求偏导,并令其为零,得到双方的最优努力水平:
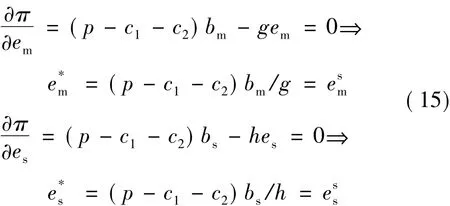
由式(15)可见,努力水平可观测情况下,对于制造商的最优解也同时使得供应链整体利润最大化,双方选择的努力水平是满足系统帕累托最优的。
3 信息不对称情况下的模型分析
3.1 规划问题求解
在信息不对称的情况下,制造商不能观测供应商的努力水平,双方都从自身利益最大化出发,以同时行动的纳什均衡来选择研发的努力水平es,em,也就是双方的努力受到激励相容约束式(6)影响。
式(6)对em求偏导并令其等于零,得:
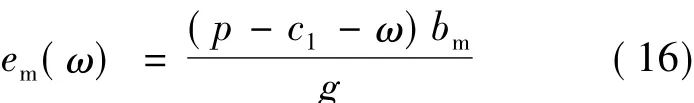
式(6)对es求偏导并令其等于零,得:
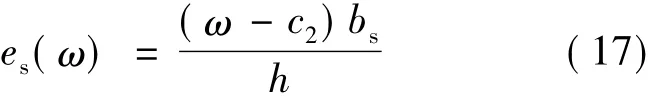
由式(16)和式(17)可见,双方选择的努力水平随制造商的产出分享ω变化而变化。由此得出以下命题:
命题1:制造商选择的努力水平em(ω)随产出分享ω的增加而减少,供应商选择的努力水平es(ω)随制造商宣布的产出分享ω的增加而增加。
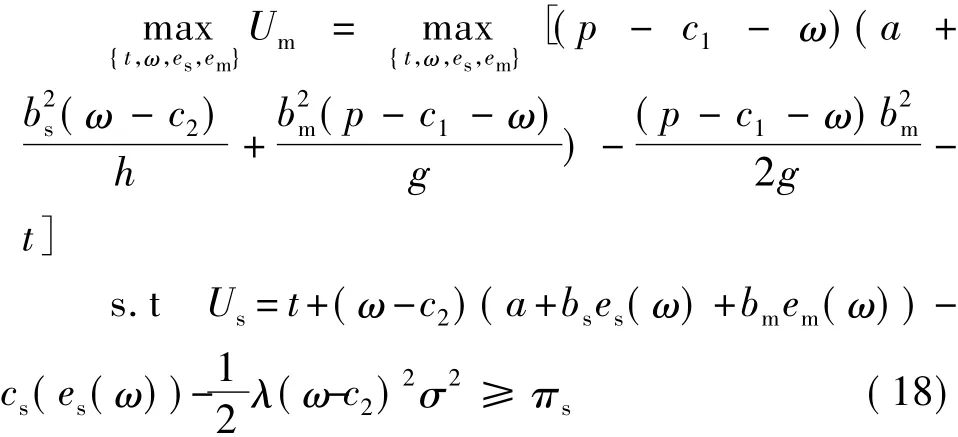
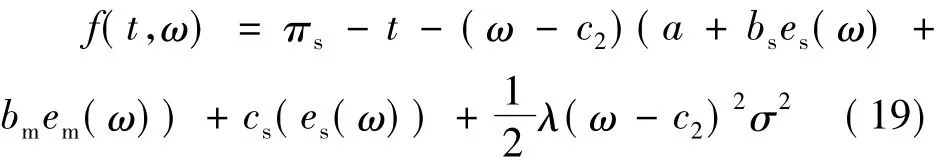
因此构造如下广义拉格朗日函数,其中λ1为不小于0的拉格朗日乘子。
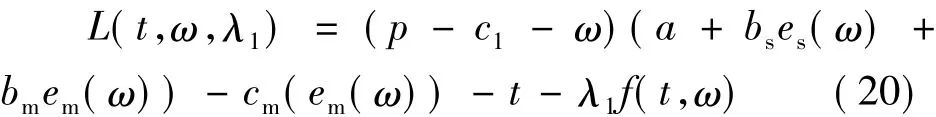
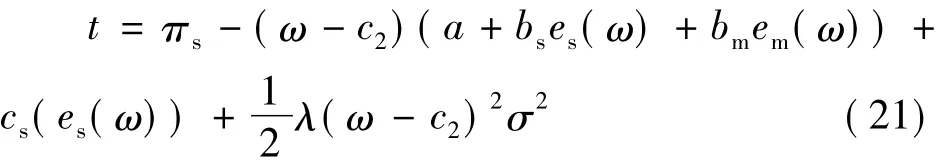
将式(21)带入到目标函数式(18)消去t,得出制造商的目标函数为:

3.2 模型结论分析
命题2:(1)若 λ→∞,则ωa=c2=0,>0,这意味着供应商一点风险承受能力都没有,制造商只需给供应商固定报酬,市场产出取决于市场条件、制造商的努力和随机变量。(2)当λ=0时,c2<ωa< p-c1,eas>0,eam>0,说明供应商为风险中性时,制造商和供应商对产品的生产开发都承担风险,所以又要产生利润分享。(3)若λ>0,由于<0,即随着风险系数的上升,激励系数ω会降低,风险规避程度会抵消激励作用;由于>0,所以随λ增大而增大,根据式(25),当λ >0时随λ增大而减小。说明供应商的风险规避程度越大,他付出努力就越小,制造商为了增加利润则需要付出更多的努力。
命题3:随着制造商努力成本系数g的增大,激励系数ωa增大,随着供应商努力成本系数h的增大,激励系数ωa减小。
证明如下:
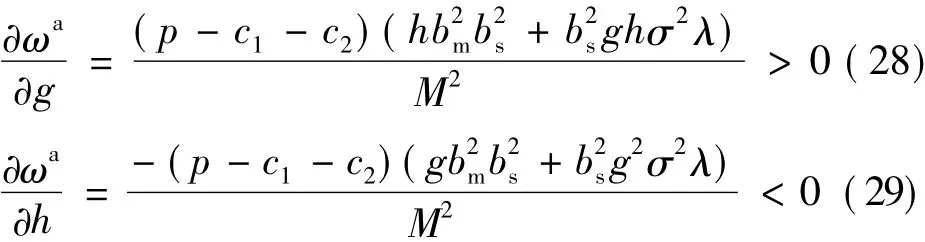
命题3说明制造商的努力成本系数越高,激励系数会越大。制造商只有这样做才能激励供应商更加努力,从而减少自己的努力成本,相反,低努力成本系数不会让其产生激励并依赖供应商努力的动机;另一方面,供应商的努力成本系数越高,制造商给予激励所产生的效应不明显,反过来导致制造商的激励懈怠,相反,供应商处于低努力成本系数时,制造商会给予更大的激励,让供应商在愿意接受的成本范围内付出更高的努力,从而减少整体的努力成本。
命题4:信息不对称的情况下,系统达不到最优。
证明:

4 算例设计
供应商努力的产出系数、努力的成本系数以及生产成本分别为 bs=0.2,h=0.3,c2=1.1;制造商努力的产出系数、努力的成本系数以及生产的成本分别为bm=0.3,g=0.4,c1=1.4;最终产品的市场价格为p=3;市场销售量为a=100;供应商的保留报酬为πs=20;市场销量的标准差为σ=0.2;供应商的风险规避系数 λ =0.5。
4.1 数值分析
通过逐步增加代入风险规避系数λ的值,计算出其他相应变量,结果见表1。
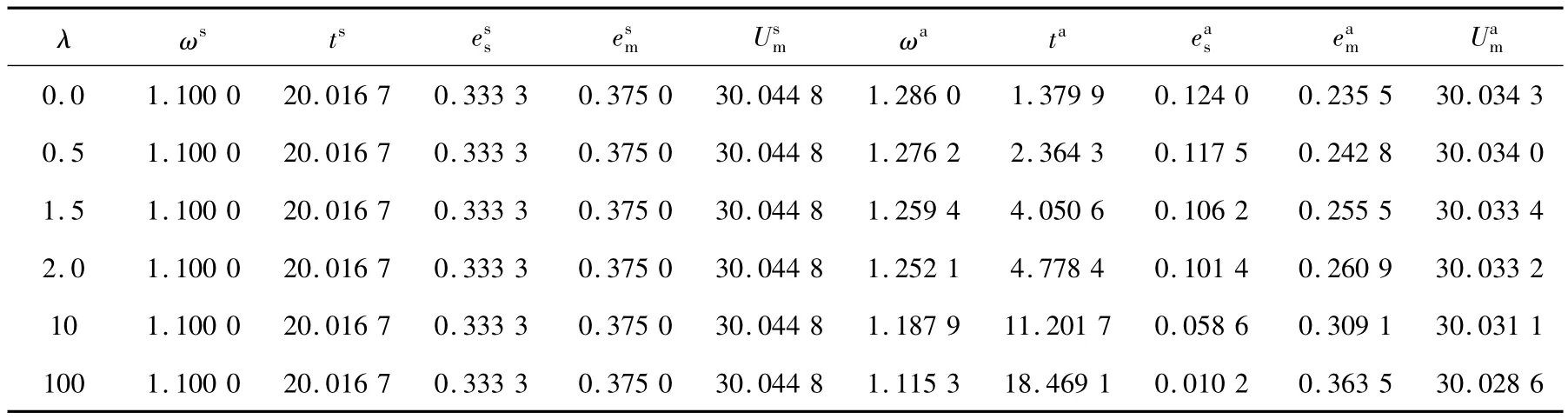
表1 风险规避系数λ变化对其余变量的影响
由表1可知,在信息对称情况下,无论供应商风险规避系数如何变化,定制契约设计中的利润分享系数与固定支付保持不变,制造商的利润也不受影响,且双方的努力程度不会变;在信息不对称的情况下,随着供应商风险规避系数递增,契约设计中的利润分享系数递减,且逐渐趋近供应商的产品成本,固定支出递增,制造商的利润递减,且供应商的努力程度递减,但是为了使得利润最大化,制造商的努力程度递增。表1结果符合命题2的结论。
通过逐步增加代入制造商成本参数g的值,计算出其他相应变量,结果见表2。
由表2可知,在信息对称的情况下,当制造商努力的成本系数递增时,定制契约设计中的利润分享系数和固定支出保持不变,制造商的利润逐渐减小,且供应商的努力程度不变,制造商的努力程度递减;在信息不对称的情况下,随着制造商努力成本系数递增,制造商为了减少自身的努力,适时提高利润分享系数,固定支出则递减,制造商的利润递减,且供应商的努力程度递增,制造商的努力程度递减。表2结果符合命题3前半部分的结论。
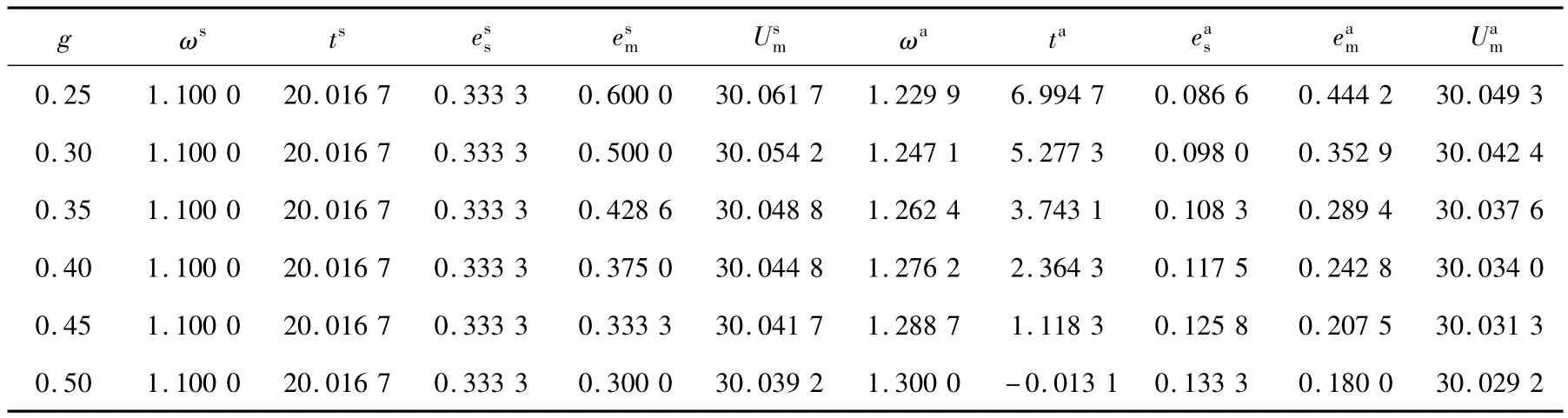
表2 制造商的成本参数g变化对其余变量的影响
通过逐步增加代入供应商成本参数h的值,计算出其他相应变量,结果见表3。
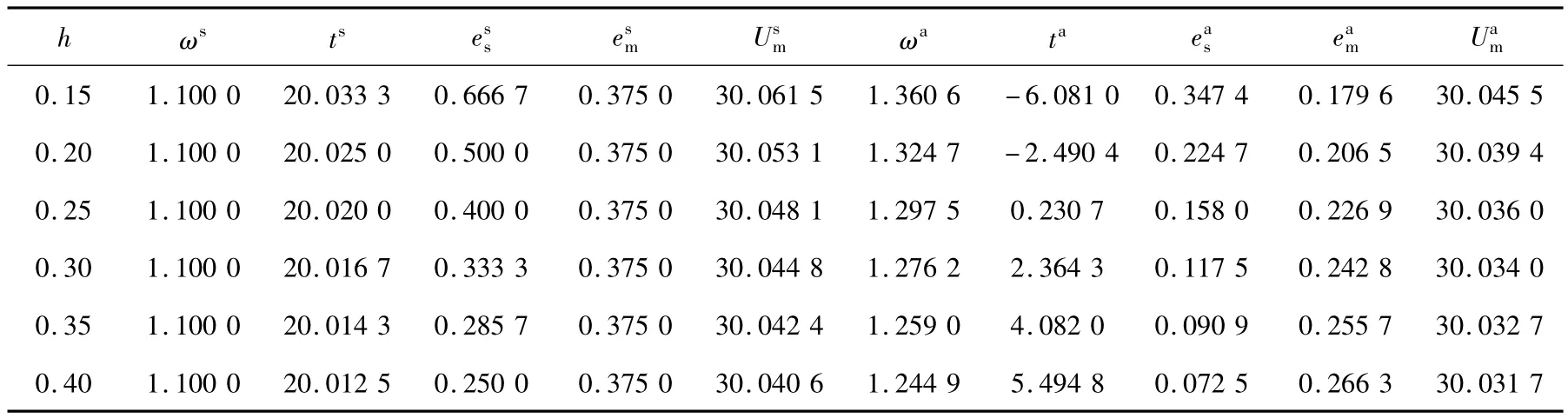
表3 供应商的成本参数h变化对其余变量的影响
由表3可知,在信息对称的情况下,当供应商的努力成本系数递增,定制契约设计中的利润分享系数不变,固定支出逐渐减小,制造商的利润也逐渐减小,且制造商的努力程度不变,供应商的努力程度递减,这与分析制造商努力成本系数对双方的的努力程度影响相对应;在信息不对称的情况下,随着供应商努力成本系数递增,制造商的激励效应减弱,站在制造商的角度会适时降低利润分享系数,固定支出则递增,在供应商成本参数较低的情况下,有可能会出现供应商反过来转移支付给制造商一定额度的情况。比如在现实连锁经营业态中,各加盟商需要上缴前期的特许加盟费、各期的特许权使用费及品牌使用费等。制造商的利润还是递减,且供应商的努力程度递减,制造商则要为保证最大化利润,提高自己的努力程度。表3结果符合命题3后半部分的结论。
综合以上3个表可以看到,信息不对称情况下,供应商选择的努力水平与利润分享系数成正向相关,而制造商选择的努力水平与定制契约中的利润分享系数成反方相关,即命题1得到验证。比较信息对称与不对称两种情况下的数据结果,信息不对称下的制造商利润明显小于信息对称的水平,可归因于信息不对称导致了制造商的信息损失。信息不对称时,受到双边道德风险影响,双方的努力程度均未达到信息对称时的水平,即系统达不到最优,会产生整体收益损失,该结论也与命题4相符。
4.2 代理成本的灵敏度分析
在已知信息不对称情况下系统达不到最优解的前提下,对于制造商而言付出的代理成本,即制造商在完全信息下和不完全信息下的效用之差与哪些因素有关呢?应先从公式的角度进行定量分析。

按照上述推导公式,运用MATLAB进行相关参数的灵敏度分析,结果如图1、图2所示。
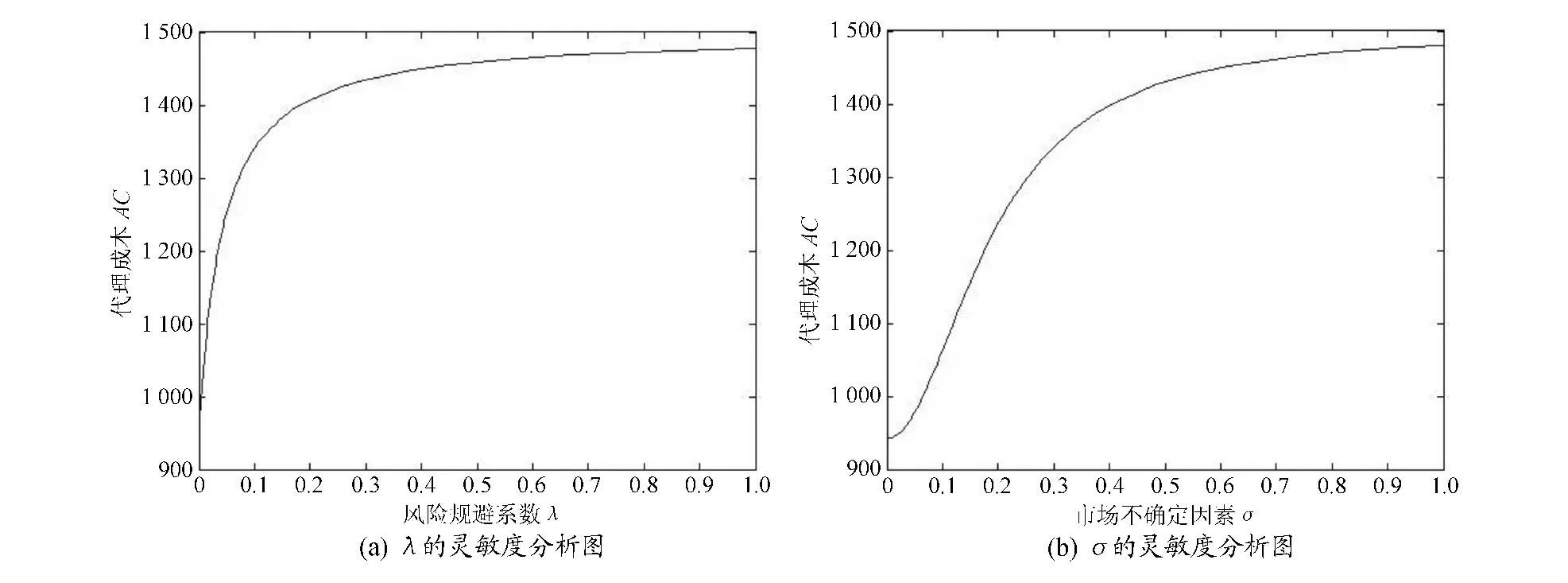
图1 代理成本对于风险规避系数λ和市场不确定因素σ的灵敏度分析
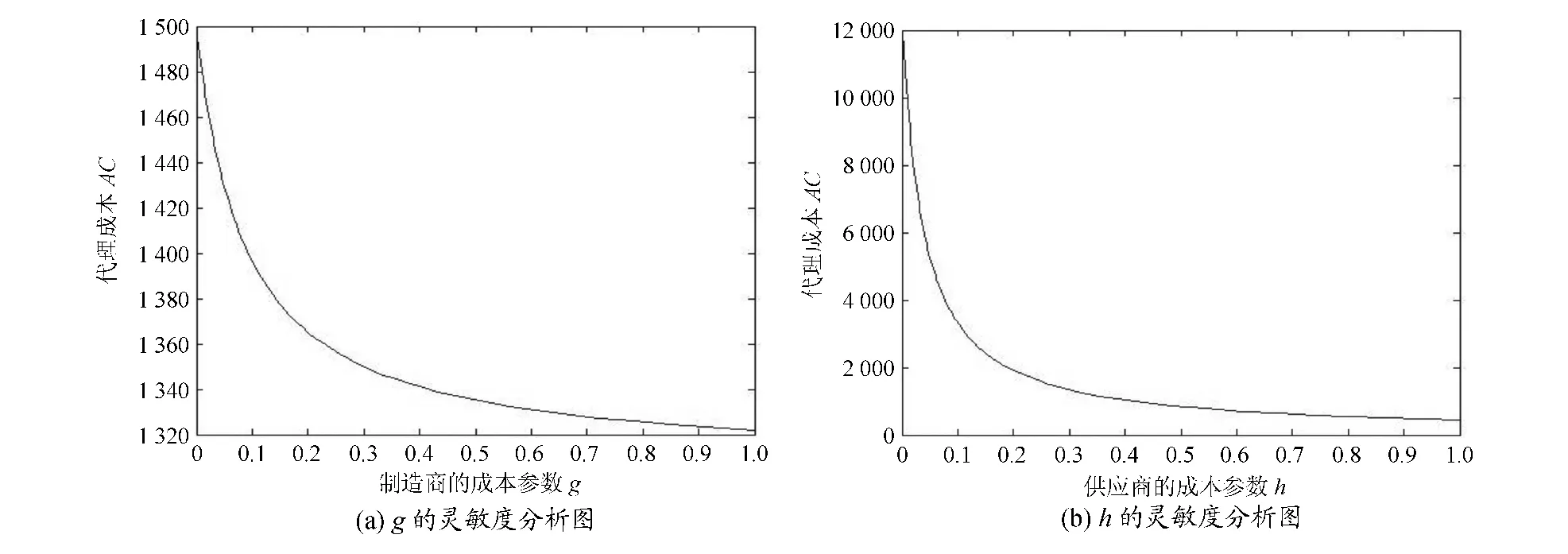
图2 代理成本对于制造商的成本参数g和供应商的成本参数h的灵敏度分析
图1 表明代理成本AC与风险规避系数λ及市场不确定因素σ都成正向关系。供应商的风险规避程度越大,制造商为鼓励他参与进契约中,需要付出的代理成本也会越大。市场环境越不确定,信息不对称情况对于占主导地位的制造商的获利能力影响越大,制造商付出的代理成本也越大。由趋势图可知代理成本值总是为正的,即对于信息不对称情况下的制造商而言总存在代理成本。
图2表明代理成本AC与g和h都成反向关系。制造商与供应商的成本参数越大,成本价值对于各自利润的影响程度越大,相对而言,双方的信息对称价值越不明显,在信息对称情况下制造商的利润水平与信息不对称情况下的效益之差越小。
5 结束语
本文在双边道德风险模型下,站在制造商的角度,研究了供应链中产品开发合作的最优线性报酬契约设计。分别在信息对称情况下和信息不对称情况下探讨了双方的成本参数及供应商的风险规避系数对于报酬契约中参数选取的影响以及最终制造商得到的利润情况。在得出信息不对称情况下系统达不到最优结论后,针对代理成本对于相关参数的灵敏度变化进行了算例分析。最终得到了一些有意义的结论:(1)信息不对称时,制造商选择的努力水平随产出分享的增加而减少,供应商选择的努力水平随制造商宣布的产出分享的增加而增加。(2)供应商的风险规避系数越大,其付出的努力就越小,而制造商为了增加利润会付出更多的努力。(3)随着制造商努力成本系数增大,报酬契约中激励系数将设计得越大;随着供应商努力成本增大,激励系数越小。(4)信息不对称的情况下,系统达不到最优。
文章在讨论信息不对称的情况时仅限于对双方努力行为的不可观测性进行讨论,在今后的研究中可以尝试就双方的单位生产成本这一私有信息方面做出不对称情况下的探讨。本文假设的前提制造商是风险中性的,未来,对于制造商的风险厌恶情况也可以做进一步的研究。
[1] Kim B.Coordinating an innovation in supply chain management[J].European Journal of Operational Research,2000,123(3):568-584.
[2] Kim B.Dynamic outsourcing to contract manufacturers with different capabilities of reducing the supply cost[J].International Journal of Production Economics,2003,86(1):63-80.
[3] Iyer A V,Schwarz L B,Zenios S A.A principal-agent model for product specification and production[J].Management Science,2005,51(1):106-119.
[4] 李小卯.信息技术外包套牢问题的研究[J].系统工程理论与实践,2002(3):26-31.
[5] Basu A K,Lal R,Srinivasan V,et al.Salesforce compensation plans:an agency theoretic perspective[J].Marketing Science,1985,4(4):267-291.
[6] Reid Jr J D.The theory of share tenancy revisited-again[J].The Journal of Political Economy,1977,28(4):403-407.
[7] Rubin P H.Theory of the firm and the structure of the franchise contract[J].Journal of Law and Economics,1978,21(1):223.
[8] Eswaran M,Kotwal A.A theory of contractual structure in agriculture[J].The American Economic Review,1985,75(3):352-367.
[9] Cooper R,Ross T W.Product warranties and double moral hazard[J].The RAND Journal of Economics,1985(16):103-113.
[10]Corbett C J,DeCroix G A,Ha A Y.Optimal shared-savings contracts in supply chains:linear contracts and double moral hazard[J].European Journal of Operational Research,2005,163(3):653-667.
[11]邓艳红,陈宏民.风险投资中的双向道德风险与帕累托有效的合约区间——讨价还价的视角[J].经济学,2006(2):923-938.
[12]李丽君,黄小原,庄新田.双边道德风险条件下供应链的质量控制策略[J].管理科学学报,2005(1):42-47.
[13]Gan X,Sethi S P,Yan H.Channel coordination with a riskneutral supplier and a downside-risk-averse retailer[J].Production and Operations Management,2005,14(1):80-89.
