基于AFKF的多传感器加权融合算法
2013-08-16周少伟李洲洋雷少坤
周少伟,李洲洋,雷少坤
(西北工业大学机电学院,陕西西安 710072)
多传感器数据融合就是把在不同位置的多个同类或不同类传感器所提供的信息综合处理,消除这些传感器间可能存在的冗余和矛盾信息,加以互补,降低测量数据的不确定性,以形成对所观测维度的完整可信的感知描述,从而提高检测系统的决策、规划、反应的快速性和正确性,降低决策风险[1-2]。
对于一个多传感器测量系统,加权平均是最简单有效的数据融合算法。加权平均法的原理是根据传感器提供测量数据精度的高低计算出各自的权重,并进行加权融合,因此可针对不同品质的同类传感器测得的动态位置数据进行实时处理。又根据Fagin等人提出的理论[3],在标准卡尔曼滤波算法基础上引入渐消因子,形成一种自适应渐消卡尔曼滤波 (Adaptive Fading Kalman Filter,AFKF)算法,对滤波系统测量值进行实时自适应修正,可提高对被测物体的动态位置实时检测的能力及鲁棒性。
本文在AFKF算法的基础上,提出基于自适应渐消卡尔曼滤波的多传感器加权融合(Weighted Fusion of Multi-sensor Information Based on Adaptive Fading Kalman Filter,WFMS-AFKF)算法,对被测物体在匀速、匀加速以及变加速运动状态下的动态位置进行精确测量。
1 WFMS-AFKF算法
1.1 AFKF 算法
对于线性离散时间系统,标准卡尔曼滤波的状态方程定义如下:
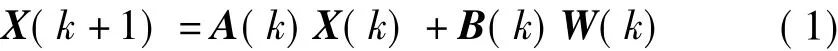
式中:X(k)为被测物体转动或移动的参数向量,X(k)=[θ ω α]T,θ为被测物体的位置,ω 为被测物体的速度,α为被测物体的加速度;A(k)为系统状态转移矩阵;B(k)为噪声输入矩阵;W(k)为系统噪声。
被测物体转动或移动位置的测量方程:
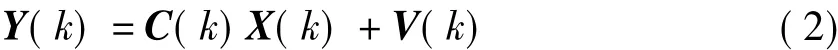
式中:Y(k)为被测物体位置测量矢量;C(k)为测量矢量;V(k)为测量噪声。
设W(k)与V(k)为互不相关零均值高斯白噪声,即满足:
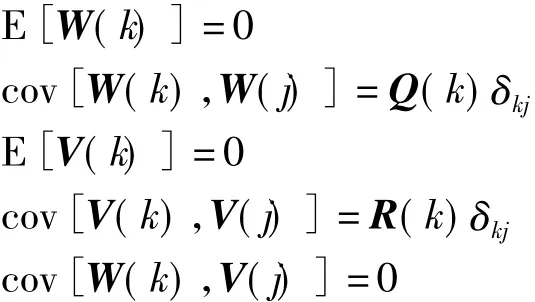
式中:Q(k)为系统噪声方差阵(非负定);R(k)为测量噪声方差阵(正定阵);δkj为狄利克莱函数。
若滤波初值X(0)是具有高斯分布的随机变量,其均值和协方差阵已知,则:
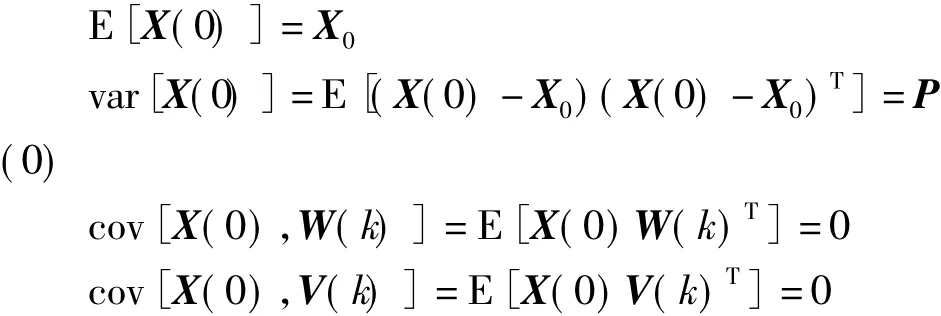
在上述条件下,卡尔曼滤波器算法如下。
预测方程:
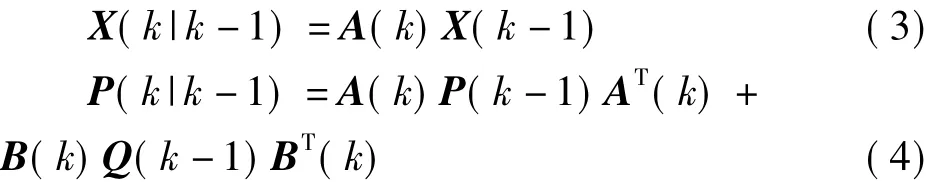
更新方程:
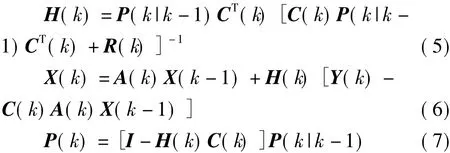
式(1)~式(7)为标准卡尔曼滤波算法(Standard Kalman Filter,SKF),因SKF算法对模型的不确定性(如加速度突变时等)比较敏感,易产生发散现象,有时会严重影响估计的精确度。因此,根据Fagin等人提出的理论,在经典卡尔曼滤波算法的预测协方差中引入渐消因子,即在式(4)中引入s(其中s>1),得:
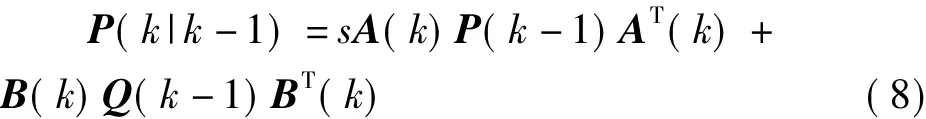
卡尔曼滤波系统是一个多元的滤波系统,即可同时获得多个动态参数,为使多个动态参数滤波后均达到最优,在预测协方差中引入渐消因子阵S(k),即

式中:S(k)=diag(s1(k),s2(k),…,sr(k)),S(k)的对角线元素均大于等于1。
式(1)~式(3)、式(5)~式(7)、式(9)一起组成了自适应渐消卡尔曼滤波算法(AFKF),对滤波系统测量值进行实时修正,提高被测物体动态位置实时检测能力及鲁棒性。
1.2 多传感器自适应加权融合算法
多传感器自适应加权融合算法的基本原理为:设有N只同类传感器独立对被测物体的同一纬度的动态位置(角位置或线位移)进行测量,对测量数据进行数据预处理后,得到第k时刻的数据分别为Y1(k),Y2(k),…,YN(k)。由于各传感器的品质不同,且受各种随机因素的干扰,Yi(k)具有随机性。以总均方误差最小为最优条件,根据传感器的测量值自适应地估计出各传感器所对应的最优加权因子,然后进行加权融合,得出Yi(k)的最优估计 ^Y(k)。则融合后的 ^Y(k)值为:

式中:Y(k)=[Y1(k),Y2(k),…,YN(k)],为测量向量;Yi(k)为第i个传感器第k时刻的测量数据;β(k)=[β1(k),β2(k),…,βN(k)],为加权向量;βi(k)为第i个传感器第k时刻的加权因子0≤βi(k)≤1。
在实际测量中,设 Yi(k)服从正态分布N(μi(k)(k)),由多元统计理论[4]可知,Y^(k)的分布密度函数为:
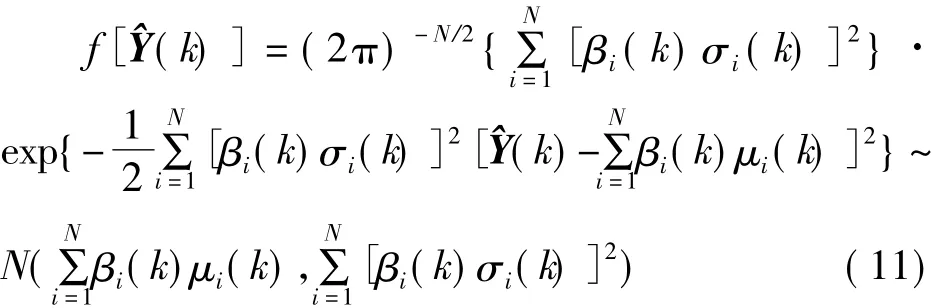
由式(11)可知,各传感器融合后的均方误差为:

1.3 最优加权因子的确定
根据多传感器自适应加权融合算法的原理可知,各传感器融合后的均方误差值越小,表明测量精度越高,即若使式(12)达到最小,则在该条件下各传感器所对应的加权因子为最优加权因子,于是构建函数:
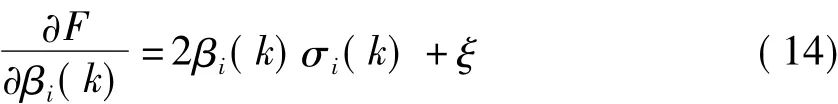
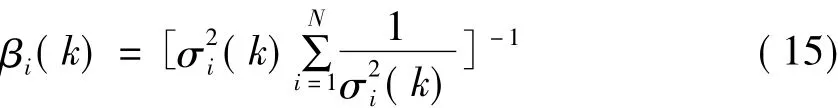
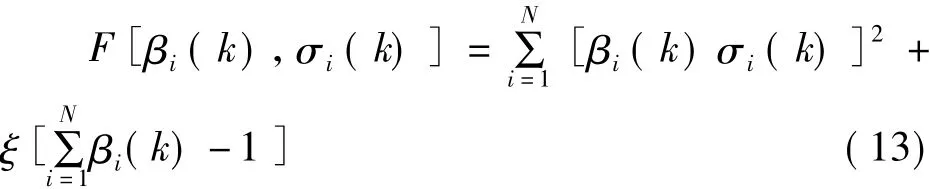
根据拉格朗日乘数法求解,对βi(k)求偏导数:
此时,对应的最小均方误差为:
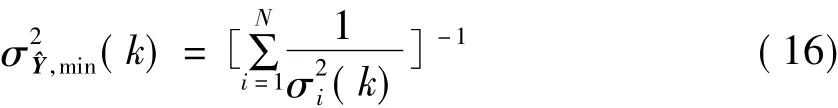
综上可知,若这N只传感器的精度相等,即σ1(k)=σ2(k)=…=σN(k)=σ(k),则融合后的精度为σ2(k)/N,这表明N只相同精度的传感器的输出数据经融合后精度可提高到单只的■N倍;若精度不等,最低精度与最高精度的均方误差分别为(k),k),则由式(16)可知
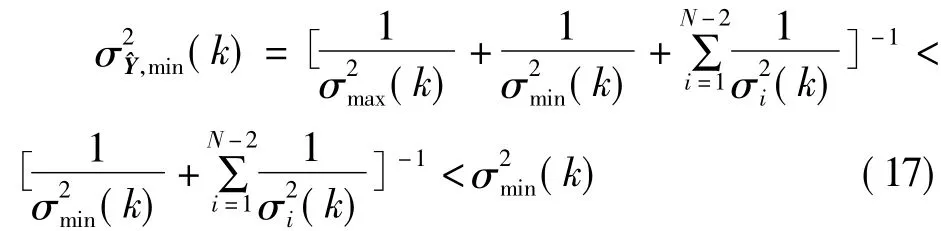
式(17)表明,当采用最优加权数据融合算法后,通过多传感器能够提高系统的测量精度。
将AFKF算法与多传感器自适应加权融合算法结合,利用AFKF算法对各个子系统进行滤波,可实时获得第i个子系统在第k时刻的位置估计值Xi(k)及协方差 Pi(k),令 Yi(k)=Xi(k),(k)等于Pi(k)对角线上第一个元素值,则由式(15)即可获得最优加权因子,进而获得最优加权融合值。图1为WFMS-AFKF算法工作原理及流程框图。
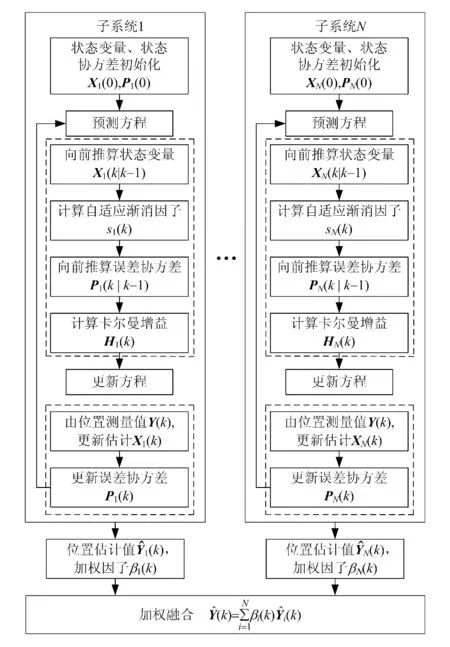
图1 WFMS-AFKF算法原理及流程框图
2 算法的应用实例
为了验证本文提出的算法,下面在工况环境下对其进行实例验证。
将传统的基于多传感器标准卡尔曼滤波融合(Multi-sensor Information Fusion Based on SKF,MSIF-SKF)算法[5]与基于本文算法的检测方法分别应用于某型卧式铆接设备中。该设备由床头、床尾、导轨及底座组成,图2为床头床尾中回转装置部分原理示意图。在上位机中从0°开始,通过每隔5°递增方式输入72个空心轴目标位置值,控制电机旋转,经过传动装置带动空心轴转动,从初位置以零速开始经过匀加速、正弦加速、匀速、正弦减速、匀减速停至下一目标值。设备在床头和床尾各采用6只MicroE公司的MercuryⅡ4000型光栅传感器对各自的空心轴进行实时测量,6只光栅传感器读数头在空心轴圆周方向进行均匀布置安装。将6组传感器测量值的实时融合值反馈到控制系统,当融合值接近一个目标位置值时,电机停止旋转,空心轴停稳后,将光栅传感器的融合值作为空心轴位置的系统测量值,使用Leica公司AT901-B型激光跟踪仪对空心轴静态位置的定位精度进行检测,将激光跟踪仪的位置数据作为空心轴位置的精确值,进行对比分析。
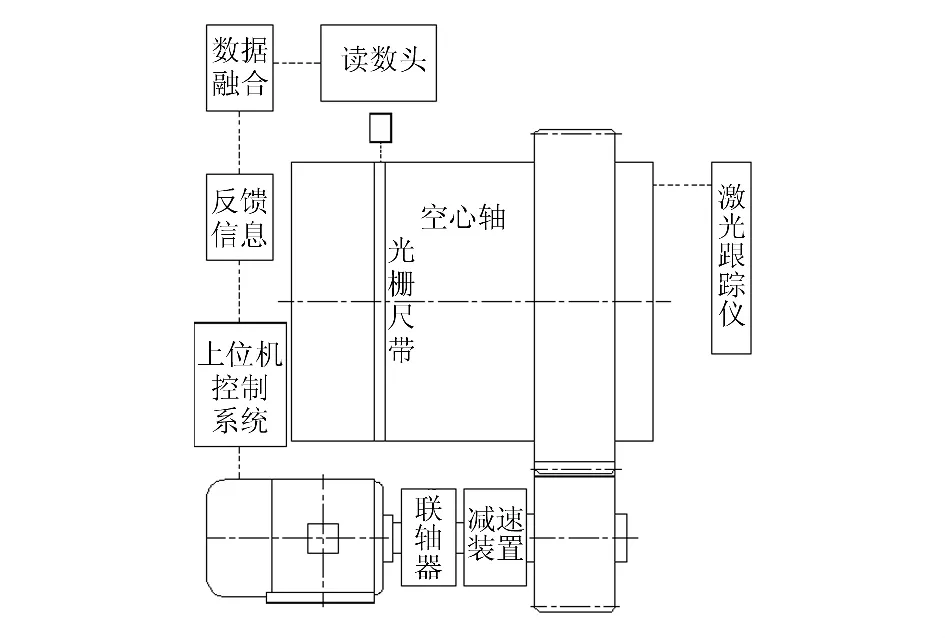
图2 床头床尾中回转装置部分原理示意图
其中初始角位移为θ=0rad,分别在匀速、匀加速及变加速转动状态下对空心轴动态位置的检测精度进行试验:(1)匀速转动,角速度ω=10-3rad/s;(2)匀加速转动,初始角速度ω=10-3rad/s,角加速度α=5×10-5rad/s2;(3)变加速转动,以正弦加速运动为例模拟,初始角速度ω=10-3rad/s,初始角加速度 α=5×10-4×sin(t/5)rad/s2。设W(k),V(k)均为高斯白噪声,取 Q(k)=10-6,Ri(k)=1.2 ×10-6,i=1,2,…,6。
表1为基于两种算法的检测测量值及采用激光跟踪仪检测的实测数据。将激光跟踪仪的位置测量值作为精确值,将基于两种算法的检测方法的测量值作为系统测量值,作误差曲线如图3所示。可以看出,基于MSIF-SKF算法的检测方法与基于WFMS-AFKF算法的检测方法的误差精度范围分别为 -148.86″~92.19″、-14.91″~10.53″。由此可以得出,基于WFMS-AFKF算法的空心轴的动态位置检测,可以有效提高其动态位置检测精度。
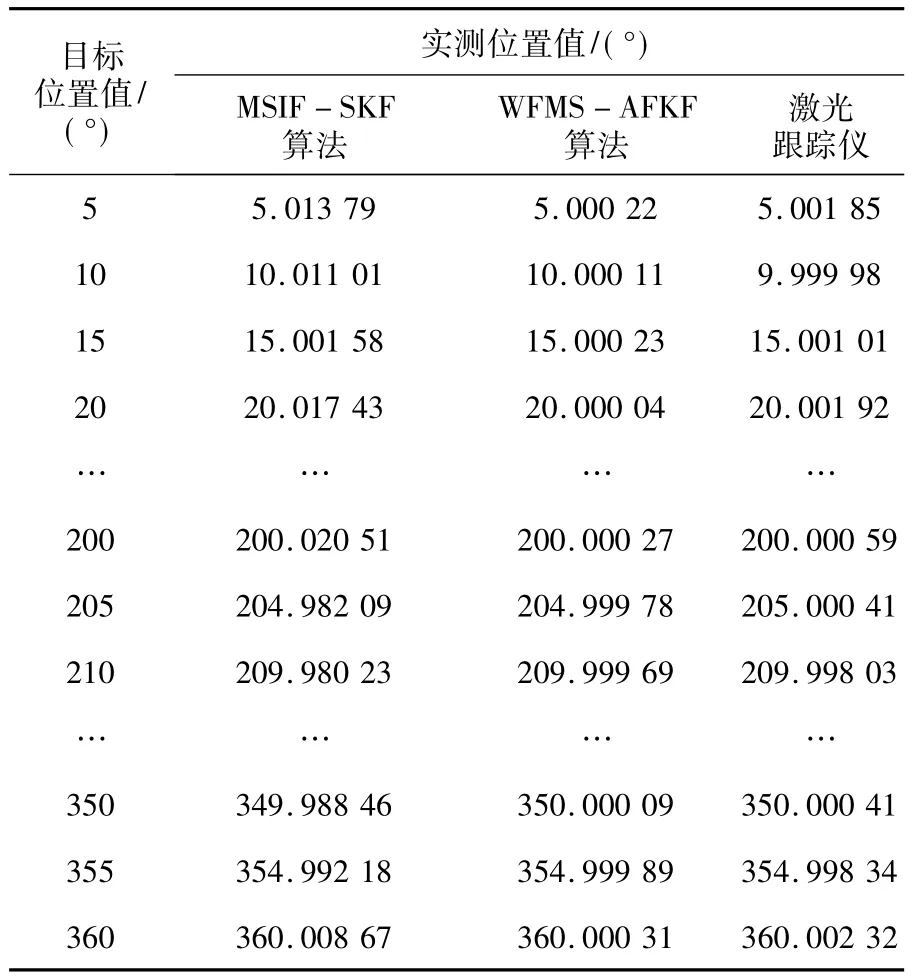
表1 基于两种算法的检测方法及采用激光跟踪仪的实测值
3 结束语
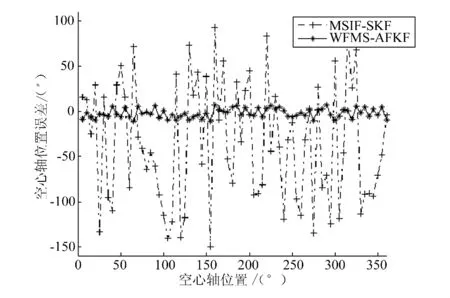
图3 基于两种算法的检测误差比较
多传感器数据融合是近几年迅速发展的一门信息综合处理技术,它将来自多传感器或是多源的信息和数据进行综合处理,从而得出更为准确可信的结论[6]。本文在AFKF算法基础上,提出基于自适应渐消卡尔曼滤波的多传感器加权融合(WFMSAFKF)算法,并对此进行了算法的实例应用验证。结果表明,与传统的MSIF-SKF算法相比,对物体进行基于WFMS-AFKF算法的动态位置检测,可以有效提高被测物体的动态位置检测精度。
[1] 蔡毅.基于信息融合理论在组合导航系统中的应用研究[D].西安:西北工业大学,2009.
[2] 陈出新.数据融合算法研究及仿真[D].西安:西北工业大学,2008:1-6.
[3] Fagin S L.Recursive linear regression theory:optimal filter theory and error analysis of optimal systems[J].IEEE Int.Convent.Record,1964(12):216-240.
[4] 张润楚.多元统计分析[M].北京:科学出版社,2010.
[5] 何友,王国宏,陆大纟金,等.多传感器信息融合及应用[M].北京:电子工业出版社,2001.
[6] 刘海斌,宫峰勋.一种改进的多传感器加权融合算法[J].电子产品世界,2009(12):19-21.
